Основные сведения о матричных операциях
Для решения задач алгебры существует огромное количество функций
встроенных в пакет Maxima. Наиболее часто используемые функции
сгруппированы в пункте меня Алгебра. Более подробно некоторые команды рассмотрим по ходу изучения материала. Номера столбцов и строк матриц начинается с единицы. При обращении к элементам матрицы указывается имя матрицы и в квадратных скобках через запятую номер строки и номер столбца. Например, A[2,3] – элемент матрицы стоящий во второй строке и третьем столбце.
Рассмотрим теперь некоторые функ-ции меню Алгебра. Команда Создать
матрицу, генерирует функцию genmatrix(fun,N,M) которая создает и заполняет матрицу, состоящую из N строк и M столбцов. Первый параметр fun определяет имя функции двух переменных fun(i,j), задающую формулу для заполнения элемента, стоящего на пересечении i-й строки и j-го столбца. Функция fun должна быть определена выше. Рассмотрим пример программы, использующей данную функцию.


В этом примере создается квадратная матрица A порядка 3, а элементы
заполняются двузначными натуральными числами первая цифра равна но-
меру столбца, а вторая – номеру строки.
Для создания и заполнения матрицы заданными числами служит ко-
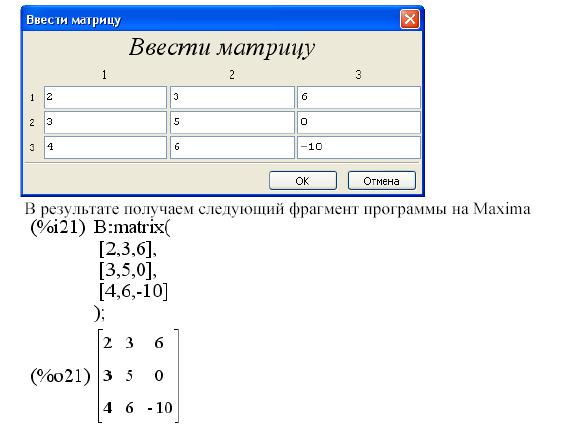
манда Вывести матрицу …Рассмотрим как ее использовать. В строке вво-
да напишем имя матрицы, например, В: и вызовем команду Алгеб-
ра/Вывести матрицу …В возникшей форме Матрица указываем число
строк, число столбцов и в качестве типа – общая. В новой форме Ввести
матрицу заполняем все элементы матрицы необходимыми значениями.
Например:
Над полученными матрицами A и B можно проводить основные ма-
тематические операции: сложения, умножения, умножения на число, ли-
нейные комбинации матриц, вычисления определителя, обращение матри-
цы, решения систем линейных алгебраических уравнений, вычисление
собственных чисел и собственных векторов.

Операция обращения матрицы A осуществляется при помощи функ-
ции invert(A), а операция матричного умножения двух матриц A и B обо-
значается точкой – A.B.

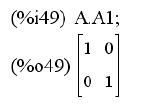
В рассмотренном примере создается квадратная матрица A второго
порядка, находится обратная матрица А1=А-1 и для проверки правильно-
сти обращения они перемножаются. В результате, как и положено, получа-
ется единичная матрица.
Для вычисления определителя матрицы A, используется функция determinant(A).
Функции eigenvalues(A) и eigenvectors(A) определяют собственные
значения и собственные вектора матрицы A, соответственно.
Функции row(A,i) и col(A,j) возвращают i-тую строку и j-тый столбец
матрицы A, соответственно.
Функция transpose (A) транспонирует матрицу A.
Существуют три варианта функции submatrix.
submatrix(i_1,…,i_k,A) – удаляет перечисленные строки в матрице A.
submatrix(A, j_1,…,j_k) – удаляет перечисленные столбцы в матрице A.
submatrix(i_1,…,i_k,A, j_1,…,j_k) – удаляет в матрице A перечисленные слева от имени матрицы строки и перечисленные справа столбцы.
Рассмотрим примеры использования данной функции.


Функция minor(A, i, j) возвращает минор матрицы A для элемента
находящегося на i-той строке и j-том столбце.
Функция rank(A) возвращает ранг матрицы A.
Функция addcol(A,B,C,…) – на базе нескольких, заранее определен-
ных матриц A, B, C и т.д., имеющих одинаковое количество строк, форми-
рует матрицу, в первых столбцах которой расположен массив A, а в после-
дующих – массивы B, C и т.д.
Пример.

Аналогичная функция addrow(A,B,C,…) – на базе нескольких, зара-
нее определенных матриц A, B, C и т.д., имеющих одинаковое количество
столбцов, формирует матрицу, в первых строках которой расположен мас-
сив A, а в последующих – массивы B, C и т.д.
Пример. Используем матрицы предыдущего примера.

Рассмотрим теперь функции, предназначенные для решения систем ли-
нейных алгебраических уравнений.
Уравнения невысокого порядка можно решить без использования мат-
риц при помощи функции linsolve, встроенной в меню Уравнения/Решить
линейную систему … Для этого необходимо подать данную команду и за-
полнить две простые формы, или непосредственно написать вызов функции
Пример. Решить систему линейных алгебраических уравнений

