Дифференциал функции и его свойства. Геометрический смысл дифференциала.

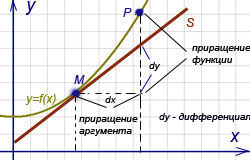
Дифференциал функции-называется главная линейная часть приращёния функции, равная произведению производной функции на приращение аргумента, и обозначается dy или df(x).

А

B

α

Т.к. а(х)-бесконечно малая =>

dy=f’(x)*∆x= f’(x)*dx

Дифференциал независимой переменной равен её приращению. dx=∆x…….………
dy- Дифференциал I порядка.

∆y= f’(x)*∆x=dy

Свойства дифференциалов

Поэтому AB= f’(x)*∆x=dy

Но согласно геометрическому смыслу производной tg α= f’(x).

Геометрический смысл дифференциала функции -в точке х равен приращению ординаты касательной к графику функции в этой точке, когда хполучит приращение ∆x.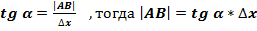

Свойства дифференцируемых функций. Теоремы Ролля, Коши, Лангранджа.

Теорема №1 (Ролль)

Пусть функция f(x) непрерывна на отрезке [a;b],дифференцируема на интервале (a;b) и на концах принимает равные значения (f(a)=f(b)), тогда существует точка c∈(a;b),в которой производная функции равна 0 (f’(c)=0).

Доказательство.

По т. Вейерштрасса (Если функция f(x) непрерывна на отрезке [a,b], то она достигает на нем своей точной верхней и нижней грани (т.е. наибольшего и наименьшего значения).)

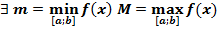
Если m=M, то f(x)=const, тогда f’(x)=0.

Пусть m≠M, хотя бы одно из значений внутри отрезка ∃ c ∈(a;b); f(c)=M

В силу теоремы верно неравенство f(c+∆x)-f(c) = 0, а ∆x→0,то

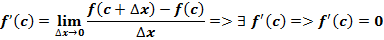
Теорема №2 (Коши)

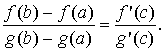Пусть функции f (x) и g(x) непрерывны на [a; b] и дифференцируемы на (a; b). Пусть, кроме того, во всех точках интервала (a; b) функция g(x) имеет ненулевую производную g ' (x) ≠ 0. Тогда существует точка c ∈ (a; b), такая, что справедлива формула.

Отношение приращений 2 функций на отрезке равно отношению значений их производных.

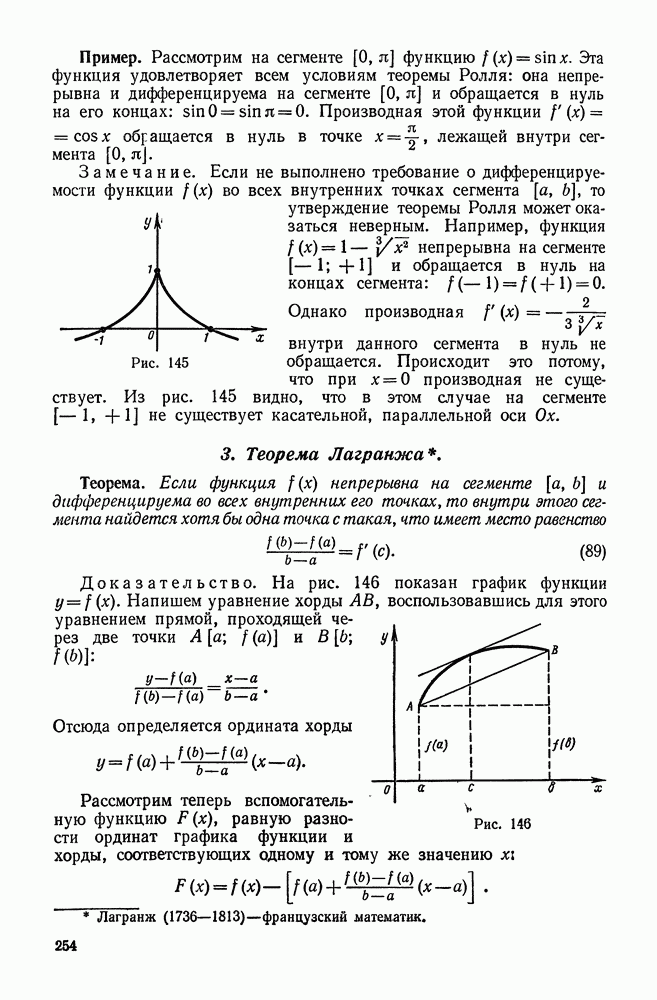
Доказательство.

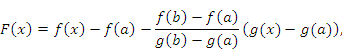
F(a)=0; F(b)=0=> удовлетворяет т.Ролля.

∃ с ∈(a;b) F'(c)=0

/

/

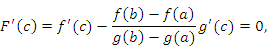Теорема №3 (Лагранж)

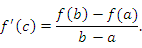Пусть функция f(x) непрерывна на отрезке [a;b],дифференцируема на интервале (a;b) и на концах принимает равные значения (f(a)=f(b)), то найдётся хотя бы точка c∈(a;b) такая, что выполняет равенство:

Доказательство.применим т.Коши
(f(b) - f(a))’=f’(c), a (b-a)’=1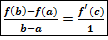

Ролль

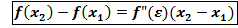
Коши

53. Раскрытие неопределённостей. ПравилоЛопиталя.

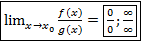
- неопределённости.

Можно применять неоднократно.

Для раскрытия неопределенностей надо заменить предел отношения двух функций пределом отношения их производных. Если окажется, что отношение производных имеет конечный предел, то к этому же пределу стремится и отношение данных функций.

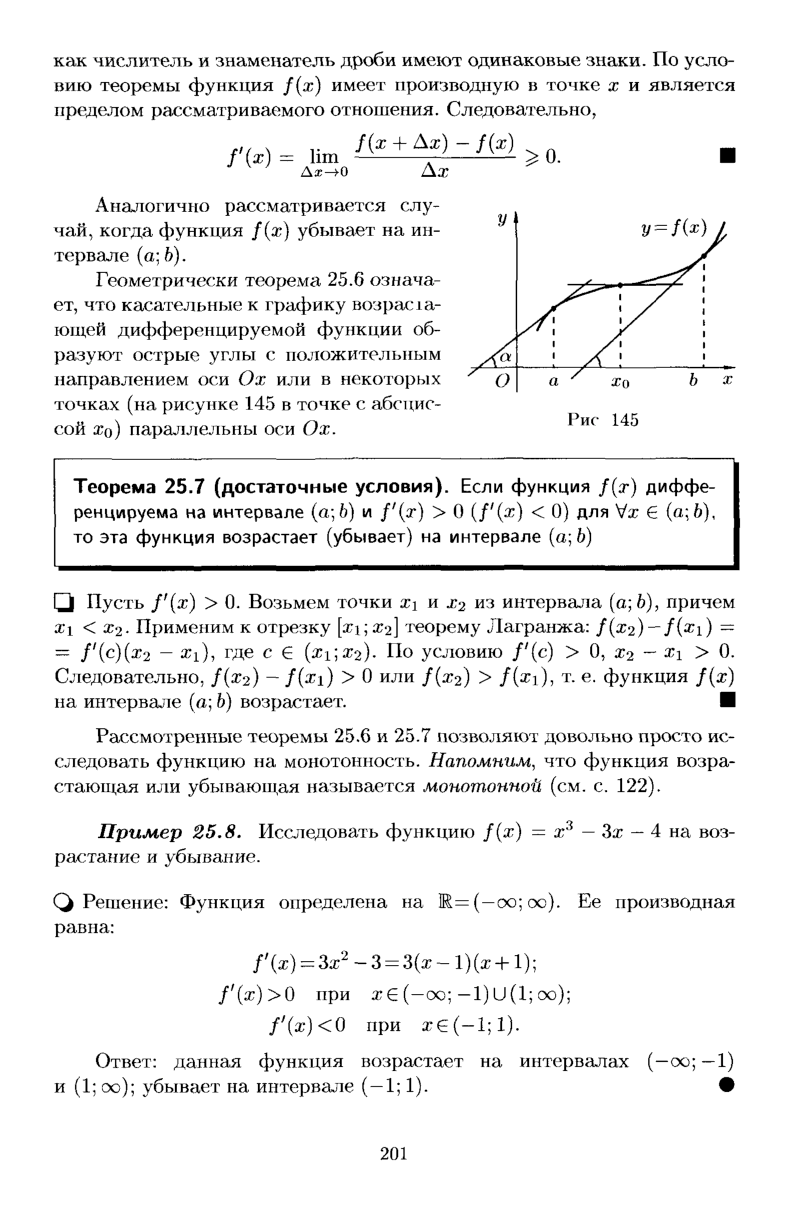54. Признаки монотонности функции.

Строго монотонная -когда постоянно воз(убыв),

Монотонная -когда не постоянно воз(убыв).

Необходимое условие экстремума.

Экстремум функции-max и min функции.

Необходимое условие экстремума -Если дифференцируемая функция y=f(x) имеетэкстремум в точкех0, то её производная в этой точке равна нулю( f'(x0)=0).Обратная теорема не верна. (у=х)

Доказательство.
пусть х0-точка max, существует неравенство:

• ∆х>0- f(x0+∆х)-f(x0)<0, т.к. x0 max, то lim≤0 lim=0

• ∆х<0- f(x0+∆х)-f(x0)<0, т.к. x0 max, то lim≥0

Достаточное условие экстремума по первым и вторым производным.