Продуктивные модели Леонтьева.

Модель Леонтьева многоотраслевой экономики (модели межотраслевого баланса)

Макроэкономика функционирования многоотраслевого хозяйства требует баланса между отдельными отраслями. Каждая отрасль, с одной стороны, является производителем, а с другой — потребителем продукции, выпускаемой другими отраслями. Возникает довольно непростая задача расчета связи между отраслями через выпуск и потребление продукции разного вида. Впервые эта проблема была сформулирована в виде математической модели в 1936 г. в трудах известного американского экономиста В. В. Леонтьева, который попытался проанализировать причины экономической депрессии США 1929-1932 гг. Эта модель основана на алгебре матриц и использует аппарат матричного анализа.

Балансовые соотношения

Для простоты будем полагать, что производственная сфера хозяйства представляет собой n отраслей, каждая из которых производит свой однородный продукт. Для обеспечения своего производства каждая отрасль нуждается в продукции других отраслей (производственное потребление). Обычно процесс производства рассматривается за некоторый период времени; в ряде случаев такой единицей служит год.

Введем следующие обозначения:

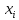‒общий объем продукции i‒ й отрасли (ее валовой выпуск);

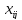‒объем продукции i‒ й отрасли, потребляемый j-й отраслью при производстве объема продукции ,

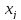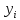‒объем продукции i‒ й отрасли, предназначенный для реализации (потребления) в непроизводственной сфере, или так называемый продукт конечного потребления. К нему относятся личное потребление граждан, удовлетворение общественных потребностей, содержание государственных институтов и т.д.

Балансовый принцип связи различных отраслей промышленности состоит в том, что валовой выпуск i‒ й отрасли должен быть равным сумме объемов потребления в производст­венной и непроизводственной сферах. В самой простой форме (гипотеза линейности, или простого сложения) балансовые соотношения имеют вид:

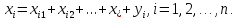(1)

Уравнения (1) называются соотношениями баланса.

Поскольку продукция разных отраслей имеет разные измерения, будем в дальнейшем иметь в виду стоимостный баланс.

Линейная модель многоотраслевой экономики

В. В. Леонтьевым на основании анализа экономики США и период перед второй мировой войной был установлен важный факт: в течение длительного времени величины 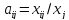меняются очень слабо и могут рассматриваться как постоянные числа. Это явление становится понятным в свете того, что технология производства остается на одном и том же уровне довольно длительное время, и, следовательно, объем потребления j-й отраслью продукции i-й отрасли при производстве своей продукции объема 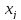есть технологическая константа.

В силу указанного факта можно сделать следующее допущение: для производства продукции j-й отрасли объема 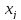нужно использовать продукцию i-й отрасли объема 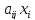, где 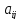‒ постоянное число. При таком допущении технология производства принимается линейной, а само это допущение называется гипотезой линейности. При этом числа 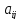называются коэффициентами прямых затрат. Согласно гипотезе линейности, имеем:

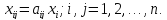(2)

Тогда уравнения (1) можно переписать в виде системы уравнений:

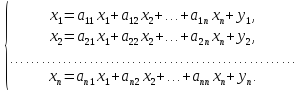(3)

Введем в рассмотрение векторы ‒ столбцы объемов произведенной продукции (вектор валового выпуска), объемов продукции конечного потребления (вектор конечного потребления) и матрицу коэффициентов прямых затрат:

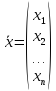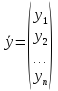, ,(4)

Тогда система уравнений (3) в матричной форме имеет вид:

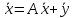.(5)

Обычно это соотношение называют уравнением линейного межотраслевого баланса. Вместе с описанием матричного представления (4) это уравнение носит название модели Леонтьева.

Уравнение межотраслевого баланса можно использовать в двух целях. В первом, наиболее простом случае, когда известен вектор валового выпуска 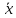, требуется рассчитать вектор конечного потребления 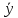‒ подобная задача была рассмотрена выше.

Во втором случае уравнение межотраслевого баланса используется для целей планирования со следующей формулировкой задачи: для периода времени T (например, год) известен вектор конечного потребления у и требуется определить вектор 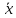валового выпуска. Здесь необходимо решать систему линейных уравнений (5) с известной матрицейA и заданным вектором 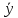. В дальнейшем мы будем иметь дело именно с такой задачей.

Между тем система (5) имеет ряд особенностей, вытекающих из прикладного характера данной задачи; прежде всего все элементы матрицы A и векторов 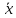и 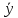должны быть неот­рицательными.

Пример:Таблица 1 содержит данные баланса трех отрас­лей промышленности за некоторый период времени. Требуется найти объем валового выпуска каждого вида продукции, если конечное потребление по отраслям увеличить соответственно до 60, 70 и 30 условных денежных единиц.

Таблица 1

№ п/п	Отрасль	Потребление	Конечный продукт	Валовой выпуск
	Добыча и переработка углеводородов
	Энергетика
	Машиностроение

Решение: Выпишем векторы валового выпуска и конеч­ного потребления и матрицу коэффициентов прямых затрат. Согласно формулам (2) и (3), имеем

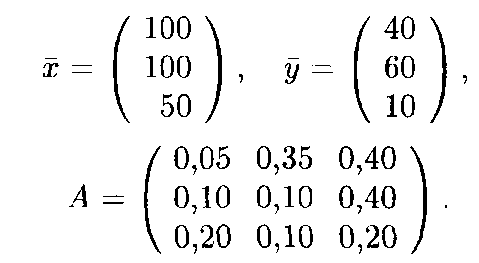
Матрица A удовлетворяет обоим критериям продуктивности. В случае заданного увеличения конечного потребления новый вектор конечного продукта будет иметь вид

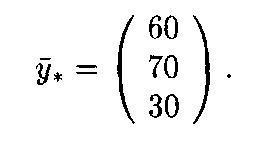(6)

Требуется найти новый вектор валового выпуска 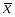_*, удов­летворяющий соотношениям баланса в предположении, что матрица Aне изменяется. В таком случае компоненты x₁, x₂, х₃ неизвестного вектора 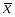_* находятся из системы уравнений, которая согласно (3) имеет в данном случае вид

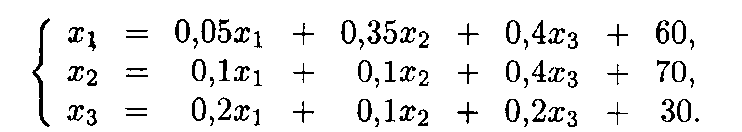
В матричной форме эта система выглядит следующим об­разом:

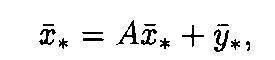(7)

или

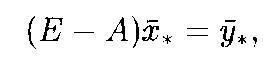(8)

где матрица (Е ‒ A) имеет вид

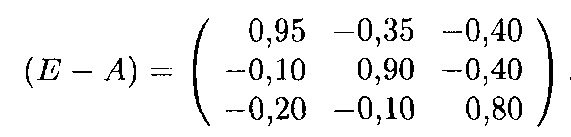
Решение системы линейных уравнений (8) при заданном векторе правой части (6) (например, методом Гаусса) да­ет новый вектор 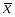_* как решение системы уравнений баланса (7):

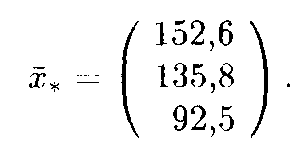
Таким образом, для того чтобы обеспечить заданное уве­личение компонент вектора конечного продукта, необходимо увеличить соответствующие валовые выпуски: добычу и пе­реработку углеводородов на 52,2%, уровень энергетики ‒ на 35,8% и выпуск продукции машиностроения ‒ на 85% по срав­нению с исходными величинами, указанными в табл. 1.

10. Собственные числа и собственные вектора.

Второй урок олинейных преобразованиях будет посвящён собственным числам и собственным значениям их матриц, и для более интересного чтения я рекомендую ознакомиться с первой статьёй. Однако если у вас совсем нет времени/сил/желания, то задачи этой страницы можно освоить и чисто формально. С небольшой художественной формальности я, собственно, и начну:

Рассмотрим произвольную квадратную матрицу, например, 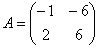. И умножим данную матрицу справа на какой-нибудь подходящий столбец. Мне пришёл в голову вектор :

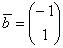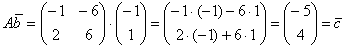
Вроде ничего примечательного – умножили матрицу 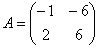на вектор-столбец 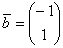и получили другой вектор-столбец 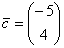. Обычная векторная жизнь. Но в обществе таких векторов существуют особые представители, которые обладают внутренним стержнем и не желают изменять себе в трудные минуты.

Умножим ту же матрицу на :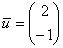

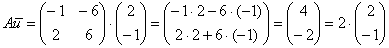
На последнем шаге вынесли константу. Что произошло? В результате умножения матрицы 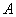на вектор 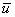, данный вектор птицей Феникс возродился с числовым коэффициентом :

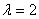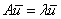
Определение: ненулевой вектор 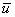, который при умножении на некоторую квадратную матрицу 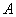превращается в самого же себя с числовым коэффициентом 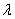, называется собственным вектором матрицы 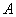. Число 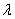называют собственным значением или собственным числом данной матрицы.

В первых абзацах статьи я выставил собственный вектор «главным действующим лицом», но на самом деле всё немного не так: говорят, что собственный вектор 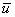соответствует собственному значению 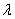. И, немного забегая вперёд, сообщу, что в практических заданиях сначала разыскиваются собственные значения и только потом собственные векторы.

Поскольку каждой квадратной матрице соответствует определенное линейное преобразование (в некотором базисе), то, исходя из содержательного смысла, часто говорят о собственных значениях и собственных векторах линейного преобразования. В Википедии есть очень удачная геометрическая интерпретация этих понятий – на репродукции Джоконды синий вектор не меняется в результате перекоса плоскости, а значит, является собственным вектором данного линейного преобразования. Я скуп на внешние ссылки, но здесь не удержался, пожалуйста, сообщите, если данную иллюстрацию вдруг удалят.

Однако не будем слишком увлекаться геометрией – сейчас в термины вектор, базис и др.вкладывается, прежде всего, алгебраический смысл. Собственные векторы и собственные значения используются во многих математических моделях, и сегодня мы освоим техническую сторону вопроса.