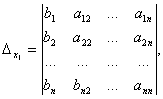
Определители высших порядков

Матрица 2-го порядка

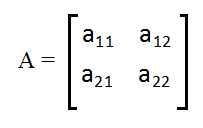
, cоставленная из четырех действительных (или комплексных) чисел называется квадратной матрицей 2-го порядка.

Определителем матрицы А, называется число

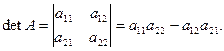
Пример № 1

Найдите определитель матрицы:

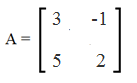
Как вы поняли из теории, чтобы найти определитель матрицы 2-го порядка достаточно найти разность произведений чисел, представленных крест-накрест:

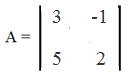
= 3*2 — 5*(-1) = 6 — (-5) = 6 + 5 = 11

Матрица 3-го порядка

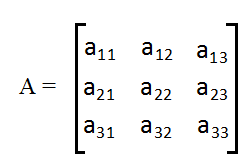
— квадратная матрица 3-го порядка

Определителем квадратной матрицы 3-го порядка, называется число

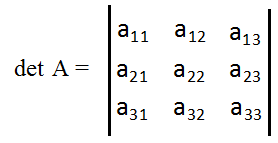
= a₁₁a₂₂a₃₃ + a₂₁a₃₂a₁₃ + a₁₂a₂₃a₃₁ – (a₃₁a₂₂a₁₃ + a₂₁a₁₂a₃₃ +a₃₂a₂₃a₁₁)

Определитель квадратной матрицы 3-го порядка вычисляется по правилу Саррюса (правило звездочки):

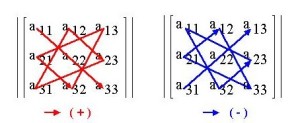
Кстати, есть небольшая хитрость в этом правиле для тех, кто боится запутаться. Заключается она в том, что нужно первые два столбца матрицы переписать за правую скобку и вы увидите, что вычислять определитель станет намного проще.

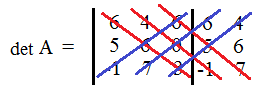
Сперва работаете с тремя красными линиями (находите сумму произведений трех линий), а после работаете с синими линиями (также находите сумму произведений, но уже синих линий). И в конце от суммы красных вычитаете сумму синих. Вот и ваш ответ. Попробуйте, это реально проще. Но я не ищу легких путей, поэтому, в основном, буду работать именно с правилом Саррюса, но вам сперва советую пользоваться данной хитростью.

Операции сложения и вычитания матриц

Сразу предупредим, что можно складывать только матрицы одинакового размера. В результате получится матрица того же размера. Складывать (или вычитать) матрицы просто – достаточно только сложить их соответствующие элементы. Приведем пример. Выполним сложение двух матриц A и В размером два на два.

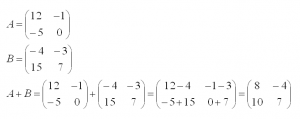
Вычитание выполняется по аналогии, только с противоположным знаком.

Умножение матрицы на число

На произвольное число можно умножить любую матрицу. Чтобы сделать это, нужно умножить на это число каждый ее элемент. Например, умножим матрицу A из первого примера на число 5:

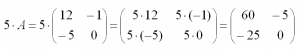
Операция умножения матриц

Перемножить между собой удастся не все матрицы. Например, у нас есть две матрицы — A и B. Их можно умножить друг на друга только в том случае, если число столбцов матрицы А равно числу строк матрицы В. При этом каждый элемент получившейся матрицы, стоящий в i-ой строке и j-м столбце, будет равен сумме произведений соответствующих элементов в i-й строке первого множителя и j-м столбце второго. Чтобы понять этот алгоритм, запишем, как умножаются две квадратные матрицы:

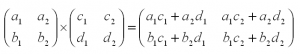
И пример с реальными числами. Умножим матрицы:

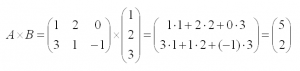
Примеры решения систем линейных уравнений методом Крамера

Пусть дана система

.

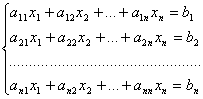На основании теоремы Крамера

………….
,

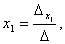
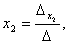
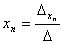где
-

определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:

Пример 2. Решить систему линейных уравнений методом Крамера:

.

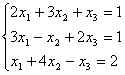Решение. Находим определитель системы:

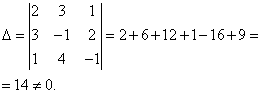
Следовательно, система является определённой. Для нахождения её решения вычисляем определители

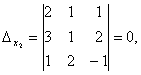
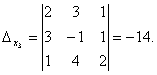
По формулам Крамера находим:

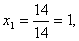
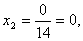
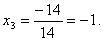
Итак, (1; 0; -1) – единственное решение системы.

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором, решающим методом Крамера.

Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.

Пример 3. Решить систему линейных уравнений методом Крамера:

.

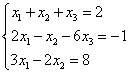Решение. Находим определитель системы:

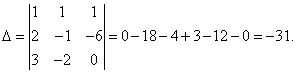
Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных

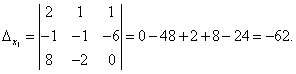
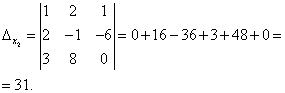
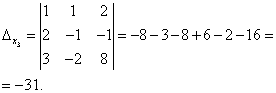
По формулам Крамера находим:

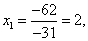
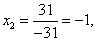
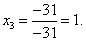
Итак, решение системы - (2; -1; 1).

6. Общая система линейных алгебраических уравнений. Метод Гаусса.

Как мы помним, правило Крамера и матричный метод непригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решения любой системы линейных уравнений, который в каждом случаеприведет нас к ответу! Сам алгоритм метода во всех трёх случаях работает одинаково. Если в методах Крамера и матричном необходимы знания определителей, то для применения метода Гаусса необходимо знание только арифметических действий, что делает его доступным даже для школьников начальных классов.

Сначала немного систематизируем знания о системах линейных уравнений. Система линейных уравнений может:

1) Иметь единственное решение.
2) Иметь бесконечно много решений.
3) Не иметь решений (быть несовместной).

Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решения любой системы линейных уравнений. Как мы помним, правило Крамера и матричный метод непригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. А метод последовательного исключения неизвестных в любом случаеприведет нас к ответу! На данном уроке мы опять рассмотрим метод Гаусса для случая №1 (единственное решение системы), под ситуации пунктов №№2-3 отведена статья Несовместные системы и системы с общим решением. Замечу, что сам алгоритм метода во всех трёх случаях работает одинаково.

Вернемся к простейшей системе с урока Как решить систему линейных уравнений?
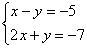и решим ее методом Гаусса.

На первом этапе нужно записать расширенную матрицу системы:
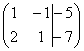. По какому принципу записаны коэффициенты, думаю, всем видно. Вертикальная черта внутри матрицы не несёт никакого математического смысла – это просто отчеркивание для удобства оформления.

Справка: рекомендую запомнить термины линейной алгебры. Матрица системы – это матрица, составленная только из коэффициентов при неизвестных, в данном примере матрица системы: 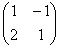. Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае: 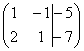. Любую из матриц можно для краткости называть просто матрицей.

После того, как расширенная матрица системы записана, с ней необходимо выполнить некоторые действия, которые также называются элементарными преобразованиями.

Существуют следующие элементарные преобразования:

1) Строки матрицы можно переставлять местами. Например, в рассматриваемой матрице можно безболезненно переставить первую и вторую строки: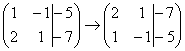

2) Если в матрице есть (или появились) пропорциональные (как частный случай – одинаковые) строки, то следует удалить из матрицы все эти строки кроме одной. Рассмотрим, например матрицу . В данной матрице последние три строки пропорциональны, поэтому достаточно оставить только одну из них: .

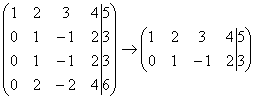3) Если в матрице в ходе преобразований появилась нулевая строка, то ее также следует удалить. Рисовать не буду, понятно, нулевая строка – это строка, в которой одни нули.

4) Строку матрицы можно умножить (разделить) на любое число, отличное от нуля. Рассмотрим, например, матрицу 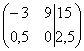. Здесь целесообразно первую строку разделить на –3, а вторую строку – умножить на 2: 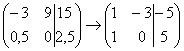. Данное действие очень полезно, поскольку упрощает дальнейшие преобразования матрицы.

5) Это преобразование вызывает наибольшие затруднения, но на самом деле ничего сложного тоже нет. К строке матрицы можно прибавить другую строку, умноженную на число, отличное от нуля. Рассмотрим нашу матрицу из практического примера: 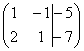. Сначала я распишу преобразование очень подробно. Умножаем первую строку на –2: 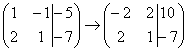, и ко второй строке прибавляем первую строку умноженную на –2: 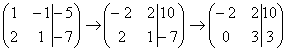. Теперь первую строку можно разделить «обратно» на –2: 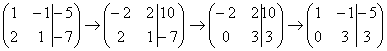. Как видите, строка, которую ПРИБАВЛЯЛИ – не изменилась. Всегда меняется строка, К КОТОРОЙ ПРИБАВЛЯЮТ.

На практике так подробно, конечно, не расписывают, а пишут короче:

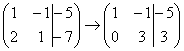
Еще раз: ко второй строке прибавили первую строку, умноженную на –2. Умножают строку обычно устно или на черновике, при этом мысленный ход расчётов примерно такой:

«Переписываю матрицу и переписываю первую строку: »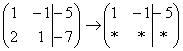

«Сначала первый столбец. Внизу мне нужно получить ноль. Поэтому единицу вверху умножаю на –2: 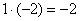, и ко второй строке прибавляю первую: 2 + (–2) = 0. Записываю результат во вторую строку: »

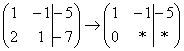«Теперь второй столбец. Вверху –1 умножаю на –2: 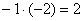. Ко второй строке прибавляю первую: 1 + 2 = 3. Записываю результат во вторую строку: »

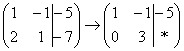«И третий столбец. Вверху –5 умножаю на –2: 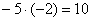. Ко второй строке прибавляю первую: –7 + 10 = 3. Записываю результат во вторую строку: »

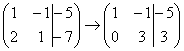Пожалуйста, тщательно осмыслите этот пример и разберитесь в последовательном алгоритме вычислений, если вы это поняли, то метод Гаусса практически «в кармане». Но, конечно, над этим преобразованием мы еще поработаем.

Элементарные преобразования не меняют решение системы уравнений

! ВНИМАНИЕ: рассмотренные манипуляции нельзя использовать, если Вам предложено задание, где матрицы даны «сами по себе». Например, при «классических» действиях с матрицами что-то переставлять внутри матриц ни в коем случае нельзя!

Вернемся к нашей системе 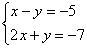. Она практически разобрана по косточкам.

Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

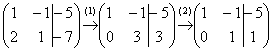
(1) Ко второй строке прибавили первую строку, умноженную на –2. И снова: почему первую строку умножаем именно на –2? Для того чтобы внизу получить ноль, а значит, избавиться от одной переменной во второй строке.

(2) Делим вторую строку на 3.

Цель элементарных преобразований – привести матрицу к ступенчатому виду: 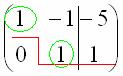. В оформлении задания прямо так и отчеркивают простым карандашом «лестницу», а также обводят кружочками числа, которые располагаются на «ступеньках». Сам термин «ступенчатый вид» не вполне теоретический, в научной и учебной литературе он часто называется трапециевидный вид или треугольный вид.

В результате элементарных преобразований получена эквивалентная исходной система уравнений:

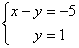
Теперь систему нужно «раскрутить» в обратном направлении – снизу вверх, этот процесс называется обратным ходом метода Гаусса.

В нижнем уравнении у нас уже готовый результат: .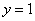

Рассмотрим первое уравнение системы 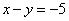и подставим в него уже известное значение «игрек»:

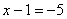
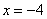
Ответ:

Рассмотрим наиболее распространенную ситуацию, когда методом Гаусса требуется решить систему трёх линейных уравнений с тремя неизвестными.

Пример 1

Решить методом Гаусса систему уравнений:

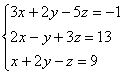
Запишем расширенную матрицу системы:

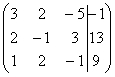
Сейчас я сразу нарисую результат, к которому мы придём в ходе решения:

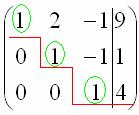
И повторюсь, наша цель – с помощью элементарных преобразований привести матрицу к ступенчатому виду. С чего начать действия?

Сначала смотрим на левое верхнее число:

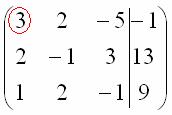
Почти всегда здесь должна находиться единица. Вообще говоря, устроит и –1 (а иногда и другие числа), но как-то так традиционно сложилось, что туда обычно помещают единицу. Как организовать единицу? Смотрим на первый столбец – готовая единица у нас есть! Преобразование первое: меняем местами первую и третью строки:

Теперь первая строка у нас останется неизменной до конца решения. Уже легче.

Единица в левом верхнем углу организована. Теперь нужно получить нули вот на этих местах:

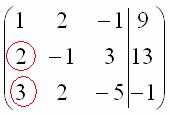
Нули получаем как раз с помощью «трудного» преобразования. Сначала разбираемся со второй строкой (2, –1, 3, 13). Что нужно сделать, чтобы на первой позиции получить ноль? Нужно ко второй строке прибавить первую строку, умноженную на –2. Мысленно или на черновике умножаем первую строку на –2: (–2, –4, 2, –18). И последовательно проводим (опять же мысленно или на черновике) сложение, ко второй строке прибавляем первую строку, уже умноженную на –2:

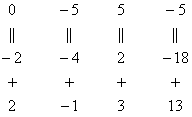
Результат записываем во вторую строку:

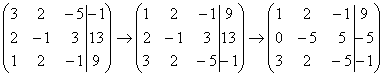
Аналогично разбираемся с третьей строкой (3, 2, –5, –1). Чтобы получить на первой позиции ноль, нужно к третьей строке прибавить первую строку, умноженную на –3. Мысленно или на черновике умножаем первую строку на –3: (–3, –6, 3, –27). И к третьей строке прибавляем первую строку, умноженную на –3:

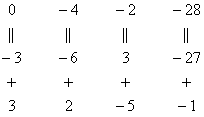
Результат записываем в третью строку:

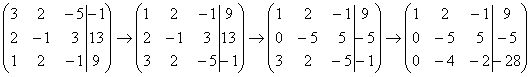
На практике эти действия обычно выполняются устно и записываются в один шаг:

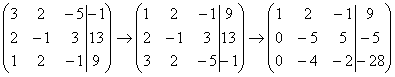
Не нужно считать всё сразу и одновременно. Порядок вычислений и «вписывания» результатов последователен и обычно такой: сначала переписываем первую строку, и пыхтим себе потихонечку – ПОСЛЕДОВАТЕЛЬНО иВНИМАТЕЛЬНО:

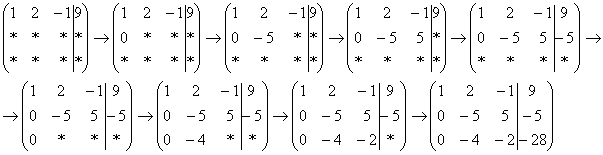
А мысленный ход самих расчётов я уже рассмотрел выше.

Далее нужно получить единицу на следующей «ступеньке»:

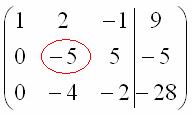
В данном примере это сделать легко, вторую строку делим на –5 (поскольку там все числа делятся на 5 без остатка). Заодно делим третью строку на –2, ведь чем меньше числа, тем проще решение:

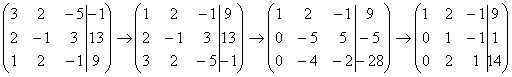
На заключительном этапе элементарных преобразований нужно получить еще один ноль здесь:

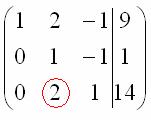
Для этого к третьей строке прибавляем вторую строку, умноженную на –2:

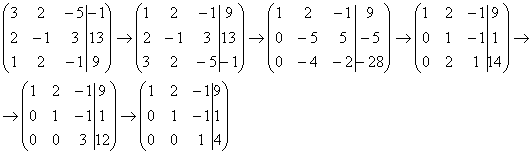
Попробуйте разобрать это действие самостоятельно – мысленно умножьте вторую строку на –2 и проведите сложение.

Последнее выполненное действие – причёска результата, делим третью строку на 3.

В результате элементарных преобразований получена эквивалентная исходной система линейных уравнений:

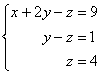
Круто.

Теперь в действие вступает обратный ход метода Гаусса. Уравнения «раскручиваются» снизу вверх.

В третьем уравнении у нас уже готовый результат: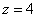

Смотрим на второе уравнение: 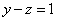. Значение «зет» уже известно, таким образом:

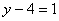
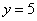
И, наконец, первое уравнение: 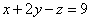. «Игрек» и «зет» известны, дело за малым:

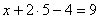
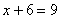
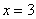
Ответ: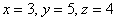

Как уже неоднократно отмечалось, для любой системы уравнений можно и нужно сделать проверку найденного решения, благо, это несложно и быстро.

Пример 2

Решить систему линейных уравнений методом Гаусса

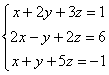
Это пример для самостоятельного решения, образец чистового оформления и ответ в конце урока.

Следует отметить, что ваш ход решения может не совпасть с моим ходом решения, и это – особенность метода Гаусса. Но вот ответы обязательно должны получиться одинаковыми!

Пример 3

Решить систему линейных уравнений методом Гаусса

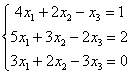
Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

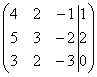
Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Я поступил так:
(1) К первой строке прибавляем вторую строку, умноженную на –1. То есть, мысленно умножили вторую строку на –1 и выполнили сложение первой и второй строки, при этом вторая строка у нас не изменилась.

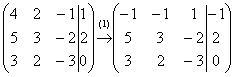
Теперь слева вверху «минус один», что нас вполне устроит. Кто хочет получить +1, может выполнить дополнительное телодвижение: умножить первую строку на –1 (сменить у неё знак).

Дальше алгоритм работает уже по накатанной колее:

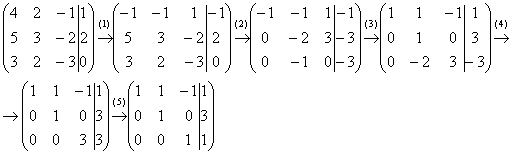
(2) Ко второй строке прибавили первую строку, умноженную на 5. К третьей строке прибавили первую строку, умноженную на 3.

(3) Первую строку умножили на –1, в принципе, это для красоты. У третьей строки также сменили знак и переставили её на второе место, таким образом, на второй «ступеньке у нас появилась нужная единица.

(4) К третьей строке прибавили вторую строку, умноженную на 2.

(5) Третью строку разделили на 3.

Скверным признаком, который свидетельствует об ошибке в вычислениях (реже – об опечатке), является «плохая» нижняя строка. То есть, если бы у нас внизу получилось что-нибудь вроде 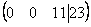, и, соответственно, 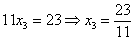, то с большой долей вероятности можно утверждать, что допущена ошибка в ходе элементарных преобразований.

Заряжаем обратный ход, в оформлении примеров часто не переписывают саму систему, а уравнения «берут прямо из приведенной матрицы». Обратный ход, напоминаю, работает, снизу вверх. Да тут подарок получился:

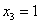
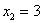
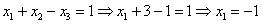
Ответ: .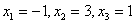

Пример 4

Решить систему линейных уравнений методом Гаусса

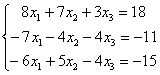
Это пример для самостоятельного решения, он несколько сложнее. Ничего страшного, если кто-нибудь запутается. Полное решение и образец оформления в конце урока. Ваше решение может отличаться от моего решения.

В последней части рассмотрим некоторые особенности алгоритма Гаусса.
Первая особенность состоит в том, что иногда в уравнениях системы отсутствуют некоторые переменные, например:

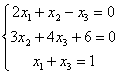
Как правильно записать расширенную матрицу системы? Об этом моменте я уже рассказывал на уроке Правило Крамера. Матричный метод. В расширенной матрице системы на месте отсутствующих переменных ставим нули:

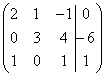
Кстати, это довольно легкий пример, поскольку в первом столбце уже есть один ноль, и предстоит выполнить меньше элементарных преобразований.

Вторая особенность состоит вот в чём. Во всех рассмотренных примерах на «ступеньки» мы помещали либо –1, либо +1. Могут ли там быть другие числа? В ряде случаев могут. Рассмотрим систему: .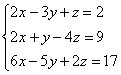

Здесь на левой верхней «ступеньке» у нас двойка. Но замечаем тот факт, что все числа в первом столбце делятся на 2 без остатка – и другая двойка и шестерка. И двойка слева вверху нас устроит! На первом шаге нужно выполнить следующие преобразования: ко второй строке прибавить первую строку, умноженную на –1; к третьей строке прибавить первую строку, умноженную на –3. Таким образом, мы получим нужные нули в первом столбце.

Или еще такой условный пример: 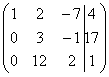. Здесь тройка на второй «ступеньке» тоже нас устраивает, поскольку 12 (место, где нам нужно получить ноль) делится на 3 без остатка. Необходимо провести следующее преобразование: к третьей строке прибавить вторую строку, умноженную на –4, в результате чего и будет получен нужный нам ноль.

Метод Гаусса универсален, но есть одно своеобразие. Уверенно научиться решать системы другими методами (методом Крамера, матричным методом) можно буквально с первого раза – там очень жесткий алгоритм. Но вот чтобы уверенно себя чувствовать в методе Гаусса, следует «набить руку», и прорешать хотя бы 5-10 систем. Поэтому поначалу возможны путаница, ошибки в вычислениях, и в этом нет ничего необычного или трагического.

Дождливая осенняя погода за окном.... Поэтому для всех желающих более сложный пример для самостоятельного решения:

Пример 5

Решить методом Гаусса систему четырёх линейных уравнений с четырьмя неизвестными.

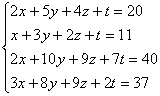
Такое задание на практике встречается не так уж и редко. Думаю, даже чайнику, который обстоятельно изучил эту страницу, интуитивно понятен алгоритм решения такой системы. Принципиально всё так же – просто действий больше.

Случаи, когда система не имеет решений (несовместна) или имеет бесконечно много решений, рассмотрены на уроке Несовместные системы и системы с общим решением. Там же можно закрепить рассмотренный алгоритм метода Гаусса.

Желаю успехов!

Решения и ответы:

Пример 2: Решение: Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду.

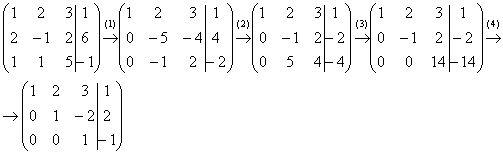
Выполненные элементарные преобразования:
(1) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на –1. Внимание! Здесь может возникнуть соблазн из третьей строки вычесть первую, крайне не рекомендую вычитать – сильно повышается риск ошибки. Только складываем!
(2) У второй строки сменили знак (умножили на –1). Вторую и третью строки поменяли местами. Обратите внимание, что на «ступеньках» нас устраивает не только единица, но еще и –1, что даже удобнее.
(3) К третьей строке прибавили вторую строку, умноженную на 5.
(4) У второй строки сменили знак (умножили на –1). Третью строку разделили на 14.

Обратный ход: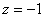

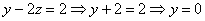
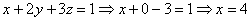
Ответ: .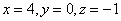

Пример 4: Решение: Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

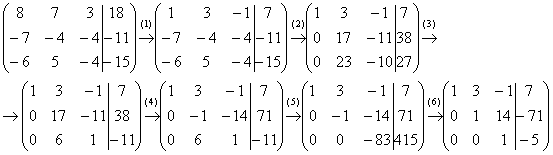
Выполненные преобразования:
(1) К первой строке прибавили вторую. Таким образом, организована нужная единица на левой верхней «ступеньке».
(2) Ко второй строке прибавили первую строку, умноженную на 7. К третьей строке прибавили первую строку, умноженную на 6.

Со второй «ступенькой» всё хуже, «кандидаты» на неё – числа 17 и 23, а нам нужна либо единичка, либо –1. Преобразования (3) и (4) будут направлены на получение нужной единицы

(3) К третьей строке прибавили вторую, умноженную на –1.
(4) Ко второй строке прибавили третью, умноженную на –3.
Нужная вещь на второй ступеньке получена.
(5) К третьей строке прибавили вторую, умноженную на 6.
(6) Вторую строку умножили на –1, третью строку разделили на -83.

Обратный ход: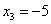

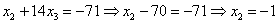
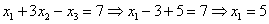
Ответ: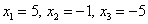

Пример 5: Решение: Запишем матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

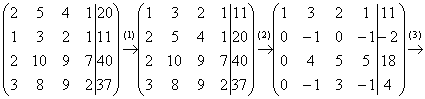
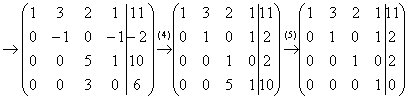
Выполненные преобразования:
(1) Первую и вторую строки поменяли местами.
(2) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на –2. К четвертой строке прибавили первую строку, умноженную на –3.
(3) К третьей строке прибавили вторую, умноженную на 4. К четвертой строке прибавили вторую, умноженную на –1.
(4) У второй строки сменили знак. Четвертую строку разделили на 3 и поместили вместо третьей строки.
(5) К четвертой строке прибавили третью строку, умноженную на –5.

Обратный ход:

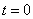
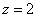
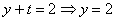
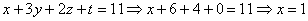
Ответ: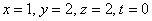

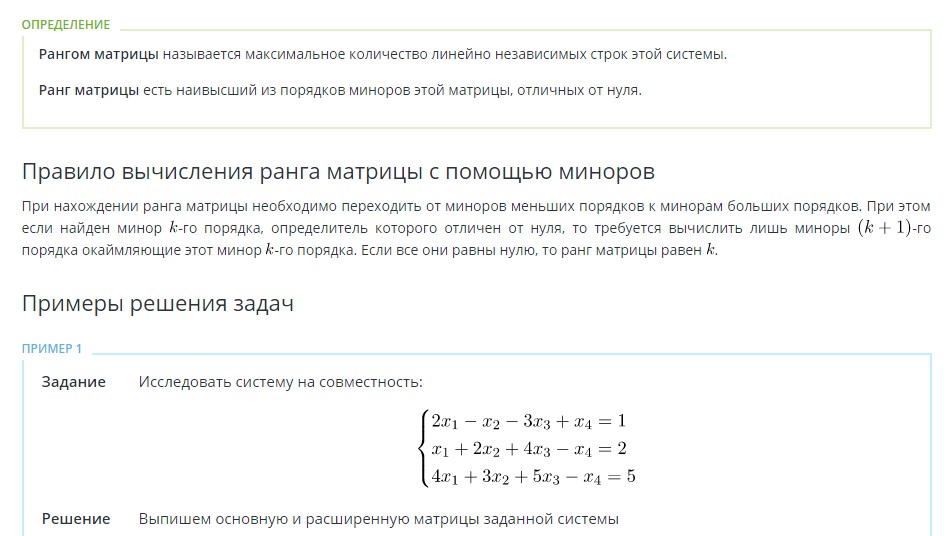
7.Ранг матрицы. Теорема Корнекера-Капелли.

8. Однородные системы

В рамках уроков метод Гаусса и Несовместные системы/системы с общим решениеммы рассматривали неоднородные системы линейных уравнений, где свободный член(который обычно находится справа) хотя бы одного из уравнений был отличен от нуля.
И сейчас, после хорошей разминки с рангом матрицы, мы продолжим шлифовать технику элементарных преобразований на однородной системе линейных уравнений.
По первым абзацам материал может показаться скучным и заурядным, однако данное впечатление обманчиво. Помимо дальнейшей отработки технических приёмов будет много новой информации, поэтому, пожалуйста, постарайтесь не пренебрегать примерами данной статьи.

Критерий Сильвестра

Нет, не Сильвестра Сталлоне :) Сначала напомню, что такое угловые миноры матрицы. Это определители 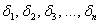которые «разрастаются» из её левого верхнего угла:

и последний из них в точности равен определителю матрицы.

Теперь, собственно, критерий:

1) если ВСЕ угловые миноры матрицы формы больше нуля, то она определена положительно, если они не отрицательны – то неотрицательно.

2) если миноры знакочередуются, причём, первый минор отрицателен, то квадратичная форма является отрицательно определённой. Если нечётные миноры неположительные, а чётные неотрицательные, то форма определена неположительно – осмысливаем, сегодня прямо какой-то день скороговорок :)

Проанализируем угловые миноры матрицы :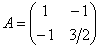

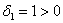, и это сразу говорит нам о том, что форма не определена отрицательно.

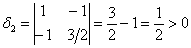
Вывод: все угловые миноры больше нуля, значит, форма 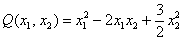определена положительно.

Есть разница с методом собственных чисел? ;)

Запишем матрицу формы 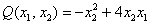из Примера 1:

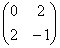
первый её угловой минор 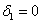, а второй 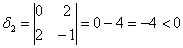, откуда следует, что форма знакопеременна, т.е. в зависимости от значений 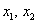, может принимать как положительные, так и отрицательные значения. Впрочем, это и так очевидно.

Возьмём форму 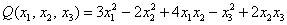и её матрицу из Примера 2:

тут вообще без озарения не разобраться. Но с критерием Сильвестра нам всё нипочём:
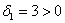, следовательно, форма точно не отрицательна.

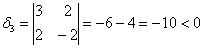, и точно не положительна (т.к. все угловые миноры должны быть положительными).

Вывод: форма знакопеременна.

Теперь разберём более занятную задачку:

Пример 4

Исследовать квадратичную форму на знакоопределенность

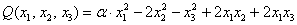
Данную форму украшает орден «альфа», который может равняться любому действительному числу. Но это ж только веселее будет, решаем.

Сначала запишем матрицу формы, наверное, многие уже приноровились это делать устно: на главную диагональ ставим коэффициенты при квадратах, а на симметричные места – споловиненные коэффициенты соответствующих «смешанных» произведений:

Вычислим угловые миноры:

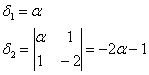
третий определитель я раскрою по 3-й строке:

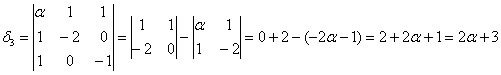
Кстати, в силу симметрии, по 3-му столбцу он раскрывается точно так же.

Дальнейшее решение удобно разбить на 2 пункта:

1) Выясним, существуют ли значения «альфа», при которых форма определена положительно или неотрицательно. Согласно критерию Сильвестра, условию положительности формы соответствует следующая система линейных неравенств:

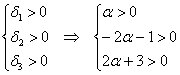
В соответствии с поставленной задачей, сначала разберёмся со 2-м неравенством:

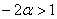
умножим обе его части на 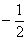, сменив у неравенства знак:
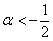, что противоречит первому неравенству системы.

Таким образом, система несовместна, а значит, форма не может быть положительной или неотрицательной ни при каких значениях «альфа».

2) Проведём исследование на отрицательность / неположительнось. Условию отрицательности формы соответствует следующая система линейных неравенств:

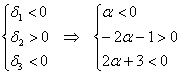
Второе неравенство уже решено: 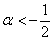, и оно не противоречит первому. И третье неравенство тоже «вписалось в рамки»: .
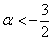Таким образом, имеем совместную систему:

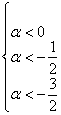
из которой следует, что форма определена отрицательно при 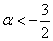. Например, если :
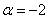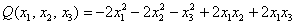– то при любом ненулевом векторе 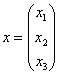данная форма будет строго отрицательна.

Осталось исследовать «пограничный» случай. Если 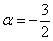, то:

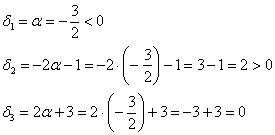
что соответствует критерию неположительности формы.

Иными словами, квадратичная форма 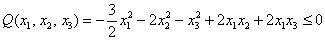, причём, нулю она равна и при некоторых ненулевых значениях .

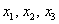Ответ: при 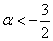форма определена отрицательно, при 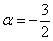неположительно, в остальных случаях форма знакопеременна.

Символическое задание для самостоятельного решения:

Пример 5

Исследовать квадратичные формы на знакоопределенность

а)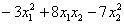

б)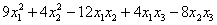

Решение и ответ рядом, после чего я жду вас на следующем уроке – о каноническом виде квадратичной формы.

Как привести квадратичную форму к каноническому виду?
Метод Лагранжа

Приветствую вас на втором уроке о квадратичных формах, который посвящен её каноническому виду и соответствующим методам. «Чайникам» и вновь прибывшим с поисковика рекомендую сначала ознакомиться первой частью – чтоб<