Некоторые сведения из теории вероятностей
Случайная величина
Дискретные случайные величины характеризуются законом распределения
| X |  |  |  | … |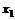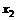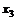
| P |  |  |  | … |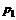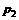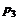
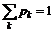. (1)
Математическое ожидание дискретной случайной величины
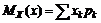. (2)
Дисперсия дискретной случайной величины
= 
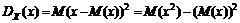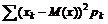. (3)
Непрерывная случайная величина характеризуется плотностью распределения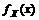 
, при этом
.
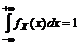Математическое ожидание непрерывной случайной величины
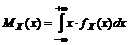. (4)
Дисперсия непрерывной случайной величины
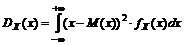. (5)
Функцией распределения случайной величины называется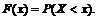 
Для непрерывных случайных величин 
.
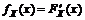Функция от случайной величины
Пусть Х- дискретная случайная величина с законом распределения (1), а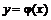 
- монотонная функция. Тогда случайная величина Y имеет закон распределения
| Y |  |  |  | … |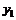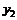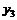
| P | | | | … |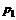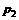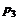
Если 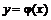- немонотонная функция, то случайная величина Y имеет закон распределения
| Y | | | | … |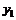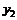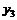
| P |  |  |  | … |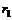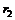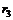
где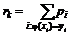 
.
Математическое ожидание функции от дискретной случайной величины
.
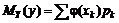Дисперсия функции от дискретной случайной величины
= 
.
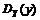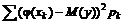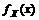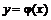Пусть Х- непрерывная случайная величина с плотностью вероятностей , а - монотонная функция. Тогда случайная величина Y имеет плотность распределения 
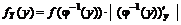. Если 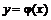- немонотонная функция, выделяем промежутки 
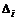, для которых 
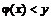. Тогда случайная величина Y имеет следующую функцию распределения
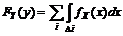
Математическое ожидание функции от непрерывной случайной величины
.
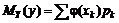Дисперсия функции от непрерывной случайной величины
= 
.
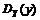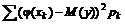Системы двух случайных величин
Ковариацией называется величина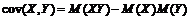 
математическое ожидание от произведения случайных величин минус произведение математических ожиданий от случайных величин. Коэффициентом корреляции называется 
.
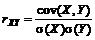Случайные величины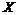 
и Y называются независимыми, если для любых реализаци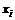й 
и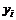 
этих величин 
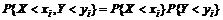. Иначе величины зависимы. Если случайные величины 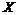и Y имеют плотности распределения 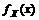и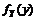 
, то их совместная плотность распределения 
.
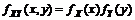Свойства математического ожидания
1. 
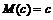, где с – некоторое число.
2. 
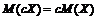, где с – некоторое число.
3. 
.
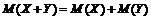4. 
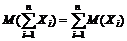, п - конечное.
5. 
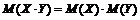, если 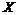и Y – независимы.
Свойства дисперсии
1. 
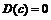, где с – некоторое число.
2. 
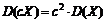, где с – некоторое число.
3. 
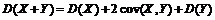, если 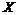и Y – зависимы.
4. 
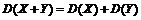, если 
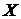и Y – независимы.
5. 
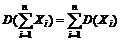, п – конечное, 
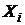попарно независимы.
Правило множителей Лагранжа
Теорема1 (правило множителей Лагранжа). Пусть функции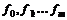 
определены в некотором параллелепипеде 
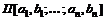, содержащем внутри себя точку 
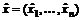, т.е. 
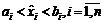. Пусть далее все функции 
, 
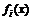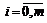и все частные производные 
, , 
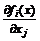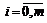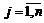непрерывны в П.
Тогда, если допустимая точка (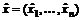 
, 
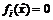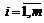) доставляет локальный экстремум (максимум или минимум) задачи
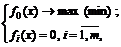
то существуют числа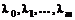 
одновременно неравные нулю и такие, что
, ,
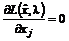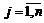где ,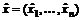 
( ), 
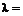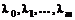– функция Лагранжа.
Теорема 2 (правило множителей Лагранжа с ограничениями типа равенств и неравенств).Если допустимая точка 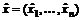доставляет локальный минимум в задачу
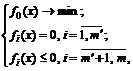
с равенствами и неравенствами, тогда найдутся числа 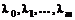одновременно неравные нулю и такие, что
, ,
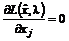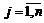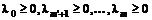- условие необратимости,
, 
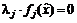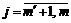- условие допускающей нежёсткости.