Эффективное множество в модели САРМ. Рыночная линия ценной бумаги
В случае безрискового заимствования и кредитования с одной и той же ставкой доходности портфели, лежащие на линейном эффективном множестве, включают в себя инвестировании в «касательный» портфель в сочетании с различным уровнем безрискового заимствования и кредитования. В САРМ каждый инвестор сталкивается с одним и тем же линейным эффективным множеством. Это означает, что все будут инвестировать в один и тот же «касательный» портфель. А из этого следует, что доля рисковых ценных бумаг в портфеле каждого инвестора будет одной и той же.
Важным свойством САРМ является то, что в состоянии равновесия каждый вид ценных бумаг имеет ненулевую долю в «касательном» портфеле. Когда прекратятся все изменения курсов, рынок займет положение равновесия. Тогда соотношение долей каждой бумаги в «касательном» портфеле в состоянии равновесия будет соответствовать соотношению долей бумаг в так называемом рыночном портфеле. Эффективное множество в САРМ состоит из инвестиций в рыночный портфель в совокупности с желаемым количеством безрискового заимствования или кредитования. Таким образом, «касательный» портфель можно определить как рыночный.
Итак, рыночный портфель – это портфель, состоящий из всех ценных бумаг, в котором доля каждой соответствует ее относительной рыночной стоимости. Относительная рыночная стоимость ценной бумаги равна ее совокупной рыночной стоимости, деленной на сумму совокупных рыночных стоимостей всех ценных бумаг. Так как этот портфель содержит все рисковые активы без исключения, он является полностью диверсифицирован. Доходность рыночного портфеля называют доходностью рынка.
Применительно к САРМ, линейное эффективное множество (рис.2.5.1) известно в САРМ как рыночная линия CML – Capital Market Line. Используя (2.4.3), уравнение рыночной линии запишется в виде
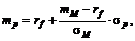 (2.7.1)
(2.7.1)
где ( 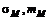 ) – соответствующие рыночному портфелю среднеквадратическое отклонение и математическое ожидание доходности.
) – соответствующие рыночному портфелю среднеквадратическое отклонение и математическое ожидание доходности.
Состояние равновесия на рынке ценных бумаг может быть охарактеризовано двумя величинами: наградой за ожидание или ценой времени (ордината точки пересечения CML с вертикальной осью, т.е. безрисковая ставка), наградой за единицу принятого риска или ценой риска (угол наклона CML).
Пример2.7.1. Определить характеристикиравновесного рынка (цену времени и цену риска), если при уровне безрисковой ставки 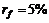 , ожидаемая доходность и среднеквадратическое отклонение рыночного портфеля равны 15 и 12%.
, ожидаемая доходность и среднеквадратическое отклонение рыночного портфеля равны 15 и 12%.
Решение. В этом случае уравнение CML будет иметь вид
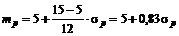 .
.
Таким образом, цена времени равна 4%, а цена риска 0,83.
Теперь определим, какие факторы влияют на доходность конкретных ценных бумаг, входящих в рыночный портфель.
Рассмотрим портфель Р, состоящий из i-ой ценной бумаги и рыночного портфеля М, в пропорции 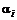 и
и 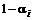 . Ожидаемая доходность такого портфеля составит
. Ожидаемая доходность такого портфеля составит
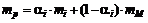 , (2.7.2)
, (2.7.2)
а стандартное отклонение будет равно
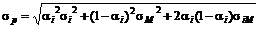 , (2.7.3)
, (2.7.3)
где 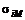 - ковариация i –ой ценной бумаги и рыночного портфеля М, которая определяется формулой
- ковариация i –ой ценной бумаги и рыночного портфеля М, которая определяется формулой
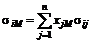 .
.
Здесь 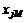 - доля бумаг j-ого вида в портфеле М, а
- доля бумаг j-ого вида в портфеле М, а 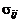 - ковариация i-ой и j-ой бумаги,
- ковариация i-ой и j-ой бумаги, 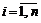 ,
, 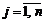 .
.
Все портфели, являющиеся комбинацией i-ой бумаги и портфеля М, лежат на некоторой кривой, структура которой описана в §2.2 главы 2.
Представляет интерес наклон этой линии. Он не является постоянным, поскольку эта линия является кривой. Из (2.7.2) следует
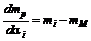 .
.
Из (2.7.3) следует
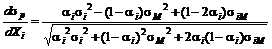 .
.
Тогда наклон кривой можно записать в виде
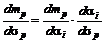
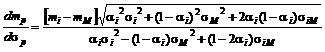 . (2.7.4)
. (2.7.4)
Портфель, для которого 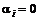 , является портфелем М. Наклон кривой в этой точке легко определить из уравнения (2.7.4)
, является портфелем М. Наклон кривой в этой точке легко определить из уравнения (2.7.4)
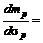
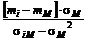 .
.
С другой сторонынаклон CML в точке М определяется из уравнения (2.7.1) как
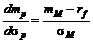 .
.
Справедливо следующее тождество
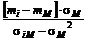 =
= 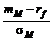 .
.
Решая уравнение относительно 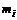 , получаем ковариационную версию уравнения рыночной линии ценной бумаги SML
, получаем ковариационную версию уравнения рыночной линии ценной бумаги SML
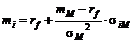 .
.
«Бета»-версия уравнения SMLимеет вид
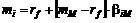 , (2.7.5)
, (2.7.5)
где 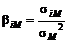 .
.
Пример2.7.2. На рынке котируются три вида акций. Определить ожидаемые доходности акций, если при уровне безрисковой процентой ставки 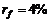 рыночный портфель
рыночный портфель 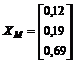 имеет математическое ожидание и среднеквадратическое отклонение, равные 22,4% и 15,2% соответственно. Матрица ковариаций имеет вид
имеет математическое ожидание и среднеквадратическое отклонение, равные 22,4% и 15,2% соответственно. Матрица ковариаций имеет вид
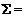
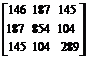 .
.
Решение. Ковариации каждой бумаги с рыночным портфелем определяются следующим образом
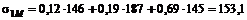 ,
,
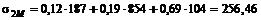 ,
,
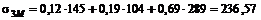 .
.
С помощью уравнения SML вычисляем ожидаемые доходности бумаг
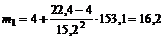 ,
,
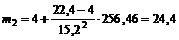 ,
,
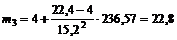 .
.
Используя уравнение SML, можно определить факт недооценки или переоценки ценной бумаги (например, акции) не только по ее доходности, но и сравнением ее действительного курса и курса в соответствии с равновесной ценой риска, которую обозначим через 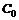 . Пусть ожидаемая в конце некоторого будущего периода цена некоторой акции (учитывая дивидендный доход) равна
. Пусть ожидаемая в конце некоторого будущего периода цена некоторой акции (учитывая дивидендный доход) равна 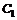 . По определению, ожидаемый доход этой ценной бумаги
. По определению, ожидаемый доход этой ценной бумаги
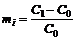 .
.
С другой стороны, воспользуемся уравнением рыночной линии ценной бумаги SML (2.7.5). Приравнивая выражения доходности по определению и по уравнению SML, получим
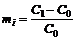 =
= 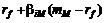 ,
,
откуда следует формула дисконтирования по безрисковой доходности, увеличенной на рисковую надбавку
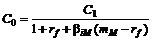 .
.
Упражнения
1. Ожидаемая доходность рыночного портфеля составляет 15%, а его среднеквадратическое отклонение 18%. Определить доходности эффективных портфелей, которым соответствует среднеквадратическое отклонение равное 12%; 15%; 20%. Безрисковая процентная ставка 4%. Изобразить точки графически.
2. Определить характеристикиравновесного рынка, если при уровне безрисковой ставки 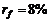 , ожидаемая доходность и среднеквадратическое отклонение рыночного портфеля равны 25% и 18%.
, ожидаемая доходность и среднеквадратическое отклонение рыночного портфеля равны 25% и 18%.
3. В условиях равновесия рынка двум эффективным портфеля соответствуют математические ожидания доходностей, равные 12% и 14% и среднеквадратические отклонения, равные 12,2% и 15,8% соответственно. Определить безрисковую процентную ставку и ожидаемую доходность рынка, если среднеквадратическое отклонение рыночного портфеля равно 14%.
4. Определить среднеквадратическое отклонение рыночного портфеля, состоящего из трех ценных бумаг
| Ценная бумага | Ковариация с рыночным портфелем | Количество |
| A | ||
| B | ||
| C |
5. Рыночный портфель состоит из трех видов акций
| Ценная бумага | «Бета» | Ожидаемые стоимости через год |
| A | 0,8 | |
| B | 0,6 | |
| C | 1,2 |
Определить истинную стоимость этих акций на настоящий момент, их ожидаемые доходности, если при уровне безрисковой ставки 4% ожидаемая доходность рыночного портфеля равна 12%.
6. Определить равновесные значения ожидаемых доходностей акций, если ожидаемая доходность рыночного портфеля 15%, безрисковая ставка 5%, «беты» акций равны 0,9 и 1,3.
7. Рыночный портфель состоит из 5 акций первого вида и 15 акций второго вида, матрица ковариаций которых имеет вид
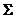 =
= 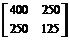 .
.
Найти «беты» этих акций.
Глава 3. Факторный анализ
Факторные модели
В факторных моделях предполагается, что доходность ценной бумаги реагирует на изменения различных факторов (индексов).
Для попыток точно оценить ожидаемые доходности, дисперсии, ковариации ценных бумаг используют так называемые многофакторные модели. Это объясняется тем, что фактически доходности по ценным бумагам оказываются чувствительными к изменению индекса рынка, к уровню процентных ставок, инфляции, темпам прироста ВВП и т.д. В случае k факторов ( 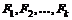 ) каждая ценная бумага будет обладать чувствительностями (
) каждая ценная бумага будет обладать чувствительностями ( 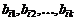 ) в следующей k –факторной модели
) в следующей k –факторной модели
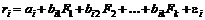 ,
,
где 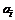 - ожидаемая доходность ценной бумаги
- ожидаемая доходность ценной бумаги 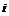 при условии, что каждый фактор имеет нулевое значение,
при условии, что каждый фактор имеет нулевое значение, 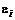 - случайная ошибка с нулевым математическим ожиданием и некоррелированная с факторами (
- случайная ошибка с нулевым математическим ожиданием и некоррелированная с факторами ( 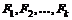 ). Причем разным ценным бумагам соответствуют различные случайные ошибки, имеющие нулевую совместную ковариацию.
). Причем разным ценным бумагам соответствуют различные случайные ошибки, имеющие нулевую совместную ковариацию.
Примером однофакторной модели может служить рыночная модель.
В случае рыночной модели предполагается, что имеется один фактор – доходность по индексу рынка. Здесь
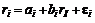 , (3.1.1)
, (3.1.1)
где
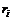 - доходность ценной бумаги
- доходность ценной бумаги 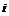 за данный период,
за данный период,
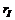 - доходность на рыночный индекс I за этот же период, случайная величина,
- доходность на рыночный индекс I за этот же период, случайная величина,
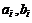 - коэффициент смещения, или нулевой фактор, и коэффициент наклона, или чувствительность к фактору, соответственно,
- коэффициент смещения, или нулевой фактор, и коэффициент наклона, или чувствительность к фактору, соответственно,
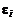 - случайная погрешность, случайная величина с нулевым математическим ожиданием.
- случайная погрешность, случайная величина с нулевым математическим ожиданием.
Случайная погрешность показывает, что факторная модель не очень точно объясняет доходности ценных бумаг.
На практике все инвесторы явно или неявно применяют факторные модели, потому что невозможно рассматривать взаимосвязь каждой ценной бумаги с другой в отдельности.
Согласно однофакторной модели (3.1.1), ожидаемая доходность ценной бумаги может быть записана в виде
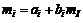 ,
,
где 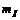 - ожидаемое значение фактора.
- ожидаемое значение фактора.
Дисперсия ценной бумаги равняется
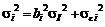 , (3.1.2)
, (3.1.2)
где 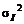 - дисперсия фактора,
- дисперсия фактора, 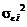 - дисперсия случайной ошибки. Первое слагаемой в формуле (3.1.2) называется факторным риском, а второе – нефакторным риском.
- дисперсия случайной ошибки. Первое слагаемой в формуле (3.1.2) называется факторным риском, а второе – нефакторным риском.
Ковариация любых двух ценных бумаг равна
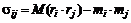 .
.
Учитывая, что 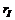 ,
, 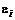 ,
, 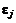 - независимы, т.е.
- независимы, т.е. 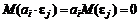 ,
, 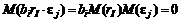 , получаем
, получаем
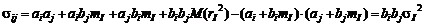 .
.
Пример 3.1.1. В рамках однофакторной модели даны две акции с доходностями
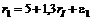 ,
,
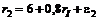 .
.
Найти ожидаемые доходности, среднеквадратические отклонения, ковариацию акций, если нефакторный риск для обеих акций равен 1%, ожидаемое значение фактора и его дисперсия равны соответственно 11% и 81.
Решение. Ожидаемые доходности акций равны
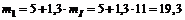 ,
,
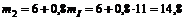 .
.
Дисперсия акций определяются формулой (3.1.2). Таким образом, среднеквадратические отклонения акций равны
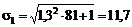 ,
,
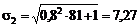 .
.
Ковариация акций равна
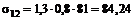 .
.
Итак, наиболее доходности акций равны соответственно 19,3% и 14,8%, среднеквадратические отклонения - 11,7% и 7,27%, ковариация – 84,24.
Определим теперь характеристики портфеля бумаг в однофакторной модели. Факторная модель портфеля определяется формулой
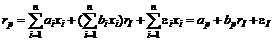 ,
,
где 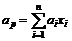 ,
, 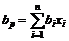 ,
, 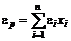 .
.
Тогда ожидаемая доходность портфеля равна
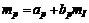 ,
,
а дисперсия
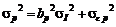 ,
,
где 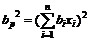 ,
, 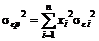 .
.
Пример 3.1.2. В рамках двухфакторной модели рассматривается портфель, состоящий из двух акций с доходностями
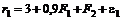 ,
,
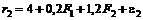 .
.
Определить дисперсии бумаг и их ковариацию, если факторы являются независимыми случайными величинами со среднеквадратическими отклонениями 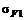 =10%,
=10%, 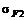 =12%, и
=12%, и 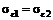 =1%.
=1%.
Решение. Дисперсия доходностей бумаг будет равна
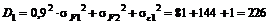 ,
,
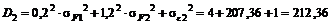 .
.
А ковариация этих бумаг равна
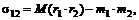
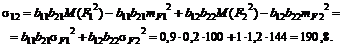
Следует иметь в виду, что факторная модель не является равновесной моделью формирования цен на финансовые активы. Сравним, например, ожидаемые доходности акций согласно однофакторной модели и модели САРМ. Согласно САРМ, свободный коэффициент 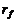 одинаковый для всех ценных бумаг, а
одинаковый для всех ценных бумаг, а 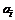 в факторной модели разный для всех активов. Теперь имеет смысл исследовать зависимость параметров
в факторной модели разный для всех активов. Теперь имеет смысл исследовать зависимость параметров 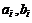 однофакторной модели и единственного параметра
однофакторной модели и единственного параметра 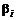 модели САРМ. Если считать, что фактор является доходностью рыночного портфеля, то ожидаемая доходность некоторой бумаги будет равна
модели САРМ. Если считать, что фактор является доходностью рыночного портфеля, то ожидаемая доходность некоторой бумаги будет равна
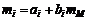 .
.
С другой стороны
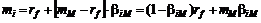 .
.
Приравнивая соответствующие коэффициенты, получаем следующую связь:
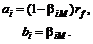
Упражнения
1. В рамках однофакторной модели акция имеет нулевой фактор, равный 5%, чувствительность к фактору, равную 0,4. Определить ожидаемое значение фактора, если ожидаемая доходность ценной бумаги составляет 12%.
2. В рамках однофакторной модели рассмотрим портфель, состоящий из двух видов акций в соотношении 1:3
| Ценная бумага | Чувствительность | Нефакторный риск |
| А | 0,5 | |
| В | 1,2 |
Найти дисперсию фактора, факторный и нефакторный риски портфеля, если дисперсия портфеля равна
а) 120;
б) 150.
3. В условиях равновесного рынка безрисковая ставка равна 4%, «бета» некоторой акции равна 0,5. Найти коэффициенты смещения и наклона однофакторной модели этой акции, если фактор является доходностью рыночного портфеля.
4. В условиях задачи 2 определить ковариацию между бумагами. Чему равно стандартное отклонение для фактора, если ковариация равна 60?
5. В рамках двухфакторной модели рассматривается портфель, состоящий из двух видов акций в соотношении 1:3 с доходностями
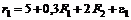 ,
,
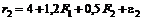 .
.
Найти ожидаемые доходности и дисперсии акций, их ковариацию, если 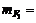 8%,
8%, 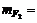 12%,
12%, 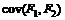 =100,
=100, 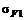 =12%,
=12%, 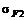 =9%,
=9%, 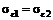 =2%.
=2%.
6. В условиях предыдущей задачи определить чувствительность портфеля, состоящего из 30 акций первого вида и 20 акций второго вида, к факторам 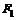 и
и 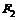 .
.
7. Ожидаемые доходности трех акций равны соответственно 17%, 18,5%, 17,5%. Нулевые факторы равны соответственно 3%, 2%, 6%.Чувствительности этих бумаг к трем факторам представлены матрицей
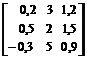 .
.
Найти прогнозируемые значения факторов.
