Определение структуры и местоположения достижимого множества
Марковиц в своей модели рассматривал портфели ценных бумаг, состоящие только из рисковых активов. Отметим на координатной плоскости, где по оси Ох будем откладывать среднеквадратическое отклонение, а по оси Оу – математическое ожидание портфеля, всевозможные точки, соответствующие всевозможным портфелям ценных бумаг существующих на рынке. Множество всевозможных портфелей сформированных из n видов ценных бумаг называется достижимым. Определим его структуру.
Рассмотрим два любых портфеля, составленных из некоторого набора бумаг, например  , со случайными процентными ставками
, со случайными процентными ставками 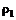 и
и 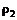 . Портфель, составленный как комбинация этих портфелей, будет иметь вид
. Портфель, составленный как комбинация этих портфелей, будет иметь вид
 .
.
А его ожидаемая доходность и дисперсия равны
 ,
, 
 ,
,
где  - коэффициент корреляции первого и второго портфеля.
- коэффициент корреляции первого и второго портфеля.
Коэффициент корреляции принимает значения от –1 до 1 включительно. Пусть  =1, тогда
=1, тогда
 ,
,
т.е.
 .
.
Прямая, соединяющая две данные точки с координатами (  ) и (
) и (  ), имеет вид
), имеет вид
 .
.
Подставляя в это уравнение точку с координатами (  ,
,  ), нетрудно заметить, что она лежит на отрезке, соединяющем соседние портфели. Для любого
), нетрудно заметить, что она лежит на отрезке, соединяющем соседние портфели. Для любого  <1 комбинация данных портфелей лежит всегда левее этого отрезка.
<1 комбинация данных портфелей лежит всегда левее этого отрезка.

Рис.2.2.1. Комбинация двух портфелей
Т.е. доказали, что  всегда выпукло вверх.
всегда выпукло вверх.
Пусть портфели, которым соответствуют точки  , состоят только из бумаг одного вида соответственно – частный случай предыдущего. Кривые
, состоят только из бумаг одного вида соответственно – частный случай предыдущего. Кривые  выпуклы вверх.
выпуклы вверх.
Предположим, что из портфелей  можно скомбинировать два портфеля
можно скомбинировать два портфеля  и
и  , имеющие одинаковые характеристики. Пусть для определённости
, имеющие одинаковые характеристики. Пусть для определённости  является комбинацией портфелей
является комбинацией портфелей  и
и 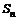 , а
, а  –
–  и
и  . Графически это показано на рис. 2.2.2.
. Графически это показано на рис. 2.2.2.

Рис.2.2.2. Построение достижимого множества
Тогда обязательно найдутся другие портфели  и
и  , составленные из
, составленные из  и
и  соответственно (рис 2.2.1), причем, портфели, являющиеся их линейной комбинацией, будут находиться левее
соответственно (рис 2.2.1), причем, портфели, являющиеся их линейной комбинацией, будут находиться левее  =
=  .
.
Таким образом, в общем случае данное множество будет иметь форму типа зонта, подобную изображённой на рис 2.2.3.

Рис 2.2.3. Достижимое множество
Упражнения
1. Дан портфель из двух ценных бумаг, доходность каждой из которых независима и равномерно распределена на интервалах  и
и  . Отметьте на плоскости точки соответствующие портфелям, состоящим из этих бумаг в соотношении 1:3, 3:1, 1:1, 2:1, 1:2.
. Отметьте на плоскости точки соответствующие портфелям, состоящим из этих бумаг в соотношении 1:3, 3:1, 1:1, 2:1, 1:2.
2. Найти прогнозируемую доходность и дисперсию портфеля, состоящего из бумаг двух видов в соотношении 1:2, 2:1, если доходности этих бумаг есть величины случайные и независимые, заданные плотностями распределения


Построить на плоскости точки, соответствующие этим портфелям.
3. Известно, что прогнозируемые доходности акций портфеля равны 5%, -10%, 25%. Привести примеры портфелей, состоящих из этих ценных бумаг, если ожидаемая доходность всего портфеля равна 10%. Отметить на плоскости точки, соответствующие этим портфелям, если задана матрица ковариаций
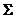 =
=  .
.
Выберите из полученных портфелей наиболее предпочтительный. Обоснуйте свой ответ.
4.Даны два портфеля, состоящие из трех видов ценных бумаг в соотношениях (2:1:2), (1:3:2), а также дан вектор средних доходностей и матрица ковариаций
М=  ,
, 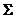 =
=  .
.
Инвестор скомбинировал свой портфель из двух данных. Отметить на плоскости данные портфели и полученный, если доли данных портфелей в новом равны:
а) 0,8 и 0,2;
б) 0,5 и 0,5;
в) 0,4 и 0,6.
