Итерационные методы вычисления корней

После отделения корней уравнения проводится их вычисление тем или иным численным методом с необходимой точностью. Наиболее используемыми являются итерационные методы, некоторые из которых будут описаны ниже.

В итерационных методах чаще всего по функции 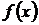в уравнении 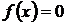строят функцию 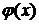такую, что искомый корень уравнения является и корнем уравнения

, (3.6)

а затем строят последовательность точек с помощью рекуррентного соотношения

, (3.7)

исходя из некоторого начального приближения корня 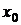, достаточно близкого к искомому корню 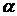. Итерационные методы, в которых функция 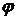не зависит от номера 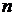, называются стационарными.

Основной характеристикой итерационных методов является скорость сходимости итерационного процесса. Итерационный метод имеет 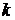-й порядок сходимости, если , где 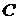– некоторая постоянная, не зависящая от 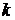. При имеет место сходимость первого порядка, или линейная сходимость, а при – второго порядка, или квадратичная. Метод является одношаговым, если для построения итерационной последовательности нужно вычислять функцию в одной точке, двушаговым – в двух и т. п.

Сравнение различных методов проводят по числу операций при реализации одной итерации и по скорости сходимости.

Метод половинного деления (дихотомии). Пусть отрезок 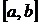есть интервал отделения корня уравнения 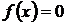и функция 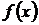непрерывна на этом отрезке. Последовательным делением получающихся отрезков пополам проводится процесс сужения интервала 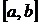так, чтобы искомый корень всегда находился внутри суженного интервала. В начале находят середину исходного интервала и вычисляют . Из двух половин исходного отрезка и выбирают тот, на концах которого функция 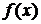принимает значения разных знаков. Затем новый отрезок также делится пополам и по знакам значений функции 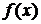на границах половинных отрезков выбирается следующий отрезок и т. д.

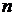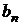Очевидно, что на -й итерации предельная абсолютная погрешность приближенного значения корня будет равна , где и 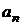– граничные точки получающегося на этой итерации интервала.

Метод дихотомии достаточно прост и надежен, всегда сходится, хотя и медленно, устойчив к ошибкам округления.

П р и м е р 3. Сузим методом дихотомии полученный в примере 2 интервал расположения действительного корня уравнения (3.5).

• Находим середину интервала . Вычисляем значения функции на концах отрезка и в его середине: , , (значения функции можно вычислять достаточно грубо, т. к. нас интересуют только знаки этих значений). По знакам значений функции выбираем интервал . Продолжая аналогично дальше этот процесс, получим: , интервал ; , интервал ; , интервал . Так как целью данного примера была только иллюстрация применения метода дихотомии, итерационный процесс обрываем. За три итерации получена абсолютная погрешность приближенного значения корня равная 0,27, что свидетельствует о медленной сходимости. •

Метод простой итерации. В методе простой итерации значение корня уточняется по рекуррентной формуле (3.7). Достаточным условием сходимости итераций является

(3.8)

вблизи корня (при этом вдали от корня это неравенство может и не выполняться). Для обеспечения сходимости часто вспомогательную функцию 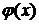представляют в виде , где коэффициент

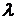
( ) подбирается так, чтобы выполнить условие сходимости

. (3.9)

Скорость сходимости метода простой итерации зависит от величины в условии (3.8): чем меньше , тем быстрее сходятся итерации. В этом методе важен также выбор начального приближения корня .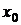

П р и м е р 4. Найти действительные корни уравнения

методом простых итераций с точностью до 0,00001.

• В примерах 2 и 3 было установлено, что данное уравнение имеет один действительный корень, расположенный на отрезке . Для упрощения начала вычислений проведем округление значений границ этого интервала, но так, чтобы эти границы не сдвинулись внутрь его (произвольное изменение границ расположения корня может привести к его потере): .

Вспомогательную функцию выбираем в виде . Ее производная . Условие сходимости (3.9) принимает вид . При необходимо выполнить условие . Последнее условие будет выполнено, если выбрать удобное для проведения вычислений значение .

Рекуррентное соотношение (3.7) будет иметь вид

В качестве начального приближения выбираем . Последовательно применяя рекуррентную формулу, получаем:

;

;

;

;

;

.

Итерации обрываем, т. к. , что меньше требуемой погрешности приближенного значения корня. Таким образом, единственный действительный корень уравнения . •

Метод Ньютона. Основное рекуррентное соотношение метода Ньютона имеет вид

. (3.10)

Предполагается, что функция 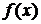в уравнении , ее первая и вторая производные непрерывны на отрезке расположения корня 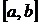, причем и сохраняют знак (монотонны).

Итерационный процесс (3.10) геометрически интерпретируется как замена на каждой итерации кривой 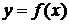на касательную к ней в точке с координатами и определение следующего приближенного значения корня как абсциссы точки пересечения касательной с осью 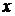(рис. 5). С этой интерпретацией связано другое название метода – метод касательных.

Достоинства метода Ньютона состоят в его квадратичной сходимости (т. е. при каждой итерации погрешность пропорциональна квадрату погрешности на предыдущей итерации), а также в том, что он является одношаговым. Однако итерационный процесс в этом методе расходится в областях, где первая производная равна нулю или принимает близкие к нулю значения.

В методе Ньютона итерации сходятся к точному значению корня при произвольном начальном приближении, но вдали от корня сходимость может быть немонотонной. Для того чтобы первое приближение 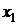не выходило из отрезка 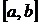и, тем самым, сходимость не ухудшалась, необходимо в качестве начального приближения 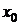выбирать в том конце отрезка, где 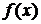и имеют одинаковые знаки.

П р и м е р 5. Найти действительные корни уравнения

методом Ньютона с точностью до 0,00001.

• Это уравнение рассматривалось выше в примерах 4, 3 и 2. Имеем , , . Основное рекуррентное соотношение в методе Ньютона в нашем случае будет иметь вид

.

При вторая производная . В качестве начального приближения выбираем левую границу отрезка, т. к. значение функции в этой точке также отрицательно. Применяя рекуррентную формулу, получаем:

;

;

;

;

.

Итерации обрываем, т. к. 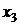и имеют одинаковые цифры уже в шестом знаке после запятой, что указывает на достижение требуемой точности. Как и в примере 4 получено значение корня . Следует также обратить внимание на более быструю сходимость, чем при применении метода простых итераций в примере 4. •

Метод секущих (хорд). Метод Ньютона, в котором решающую роль играет касательная к кривой, является предельным случаем более старого способа, в котором вместо касательной используется секущая (хорда) (рис. 6). За первое приближение корня принимается точка пересечения секущей с осью :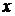

.

Затем вычисляется и, если и будут иметь одинаковые знаки, дальнейшее уточнение корня продолжают по рекуррентной формуле

.

Если же и будут иметь разные знаки, то используют рекуррентную формулу

Условия сходимости метода секущих аналогичны условиям метода Ньютона. Особенности метода:

· В методе не требуется непосредственного вычисления производной , что может существенно уменьшить объем вычислений;

· Метод является двухшаговым;

· В знаменателях вышеприведенных рекуррентных формул стоят разности величин ( ) и ( ), которые имеют вблизи корня малые и близкие значения, что может привести к большой потере точности при вычислениях, особенно для кратных корней.

Метод хорд, как и все итерационные методы, устойчив к вычислительным ошибкам: ошибка в промежуточном вычислении автоматически исправится при следующей итерации. Но заключительные вычисления необходимо проводить строго, с сохранением нескольких запасных знаков.

3. Непрерывные схемы решения нелинейных уравнений.

Итерационные методы решения нелинейных уравнений можно разбить на две группы:

* дискретные схемы решения,

* непрерывные схемы решения.

Дискретные схемы решения были рассмотрены выше. Заметим, что основными недостатками вышеперечисленных методов являются:

· зависимость от начальных условий или от интервала нахождения корня;

· сравнительно низкая скорость сходимости;

· нет правил перехода от корня к корню уравнения в случае, если их несколько.

При применении непрерывных схем для решения уравнения процесс нахождения корней осуществляется путем решения соответствующего обыкновенного дифференциального уравнения

(2.22)

Пусть определена и монотонна при и существует конечная производная 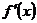. Задачу нахождения корней уравнения (2.1), являющуюся непрерывным аналогом метода простых итераций, можно рассматривать как предел при решения задачи Коши

(2.23)

если этот предел существует. Обозначим через решение задачи Коши (2.12), - искомое решение уравнения (2.1). Тогда должно иметь место тождество . Вводя обозначение для отклонения и, вычитая из (2.23) последнее уравнение, имеем

. (2.24)

Разлагая в ряд Тейлора в окрестности точки с сохранением линейных членов и подставляя полученное выражение в (2.24), получаем дифференциальное уравнение в отклонениях , решение которого имеет вид

(2.25)

Видим, что условием сходимости к корню является требование , так как в этом случае при , и, следовательно, . Считая, что монотонна при , последнее уравнение можно распространить на всю рассматриваемую выше область. Таким образом, условием применения непрерывной схемы метода простых итераций (2.23) является

(2.26)

Непрерывные схемы решения обладают более высокой скоростью сходимости и более высокой точностью решения по сравнению с соответствующими дискретными схемами. Но проблема зависимости от начальных условий и отсутствие правил перехода от корня к корню в случае, когда уравнение (2.1) имеет более одного решения, остается открытой.

Как видно из дифференциального уравнения (2.23) и уравнения (2.1) левая часть последнего заменяется производной . Данная замена является грубым приближением решения задачи (2.23) к решению задачи (2.1). Это влечёт за собой не только большую погрешность при вычислениях, но и к снижению скорости расчётов.

Перепишем уравнение (2.1) в виде

, (2.27)

где - малый параметр, .

Переход от задачи (2.1) к задаче (2.27) теоретически обоснован, так как интегральные кривые, являющиеся решением уравнения с малым параметром (2.27), проходят через все решения уравнения (2.1). Задачу нахождения корней этого уравнения непрерывным сингулярным аналогом метода простых итераций можно рассматривать как предел при и решения задачи Коши вида

(2.28)

если этот предел существует.

Проводя рассуждения, аналогичные рассуждениям, приведенным выше, получим, что решение уравнения (2.27) в точке будет иметь вид:

(2.29)

При этом, в силу того, что , то условие сходимости (2.26) останется прежним.

Полученная модификация классических схем решения не зависит от начальных условий и обладает более высокой точностью решения. Для доказательства более быстрой скорости сходимости предположим, что применение итерационных методов никогда не дает точного решения и введем точность решения . Моменты нахождения решений с точностью классическими и модифицированными методами обозначим как и . Используя решения (2.24) и (2.29), запишем неравенства вида

,

.

Из соотношений видно, что и . Сопоставляя полученные значения и , видим, что , т.е. скорость сходимости при решении задачи модифицированными методами в раз выше, чем классическими.