Действия с приближенными величинами

Источники погрешности результатов вычислений. Классификация погрешностей. При проведении вычислительной работы важно уметь оценивать точность получаемых результатов, ведя постоянный учет ошибок.

Причин возникновения ошибок много. Во-первых, исходные данные для практической вычислительной задачи часто являются результатом наблюдений, а любое измерение может дать результат с ограниченной точностью. Во-вторых, в процессе вычислений приходится использовать иррациональные числа, такие, например, как 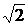, , 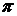, 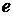которые, как известно, выражаются бесконечными непериодическими дробями. Такие числа при вычислениях могут быть представлены только приближенно. В-третьих, во многих вычислительных методах точный результат может быть достигнут только после бесконечного числа шагов. Так как, очевидно, это практически осуществить нельзя, необходимо будет остановиться на каком-то шаге, не достигнув точного значения искомой величины (например, при вычислении суммы ряда ограничиваются суммой конечного числа его первых членов). В-четвертых, уже при проведении таких простейших операций, как умножение и деление, количество разрядов получаемых чисел может возрасти настолько, что некоторое количество этих разрядов будет отброшено даже в компьютерах. Наконец, исходные погрешности будут последовательно переходить, преобразовываясь, от операции к операции и порождать новые погрешности.

Влияние погрешностей на точность результата может оказаться значительно большим, чем это обычно представляют даже при не очень сложных вычислениях. Пусть, например, требуется вычислить 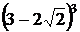. Но

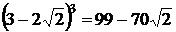. Подсчитаем эти два выражения, взяв за приближенные значения 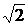три числа: 1,4; 1,41 и 1,414. Так как 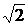=1,4142135624…, то каждое из выбранных значений довольно близко к точному и третье из них точнее. Результаты вычислений приведены в таблице:

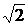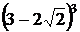		99-70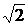
1,4	0,008
1,41	0,005832	0,3
1,414	0,005088	0,02

Получены значительно отличающиеся друг от друга результаты и непонятно сразу, какой из них ближе к верному. Из приведенного примера видно, с какой осторожностью нужно обращаться с приближенными числами.

При работе с приближенными величинами приходится решать следующие задачи:

· Давать математические характеристики точности приближенных величин;

· Оценивать точность результата, когда известна точность исходных данных;

· Определять точность исходных данных, обеспечивающих требуемую точность результата;

· Согласовывать точность различных исходных данных с тем, чтобы не затрачивать излишней работы при отыскании или вычислении одних данных, если другие данные слишком грубы;

· Следить в процессе вычислений за точностью промежуточных результатов, с тем чтобы, с одной стороны, обеспечить необходимую точность окончательного результата и, с другой стороны, по возможности упростить вычисления.

Погрешности классифицируются на погрешности округления, неустранимую погрешность и погрешность метода.

Погрешность округления возникает при замене данного числа другим, представляющим его приближенно.

Исходные данные, как правило, не являются абсолютно точными. При измерениях величин получают не их истинные значения, а некоторые доверительные интервалы, в которых они находятся с тем или иным уровнем надежности. Эти интервалы называют также областями неопределенности. В результате вычислений, в которых задействованы такие исходные данные, будут получены не точные значения искомой величины, а опять же некоторая область неопределенности для этой величины, даже если все последующие вычисления производились точно, без округлений. Границы этой области и определяют неустранимую погрешность.

Погрешность метода не зависит ни от погрешностей исходных данных, ни от округления чисел, ни от точности вычислений. Как уже говорилось выше, для решения задачи

производится замена пространств и и функции некоторыми другими пространствами и и функцией 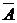, более удобными для вычислительных целей. Поэтому даже при точных исходных данных и при точных вычислениях с этими данными решается задача, отличающаяся от первоначальной. Естественно, и решение будет отличаться от точного решения исходной задачи. Это отклонение и называется погрешностью метода.

Характеристики точности чисел.

Разность

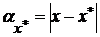, (2.1)

где - истинное значение величины, а 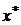- ее приближенное значение, с которым производятся вычисления, называется абсолютной погрешностью величины 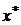. Абсолютная погрешность имеет ту же размерность, что и сама величина. Она представляет только теоретический интерес, так как точное значение в большинстве случаев не известно. Но можно найти границы, в переделах которых изменяется абсолютная погрешность. Эти границы определяются тем способом, которым получено приближенное значение 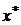. Так, при измерении длины обычной ученической линейкой, можно считать, что модуль абсолютной погрешности получаемых значений длин не будет превышать 0,5 мм. При измерениях штангенциркулем или микрометром получаем соответственно, что абсолютные погрешности не будут превышать по модулю 0,1 и 0,01 мм. При замене иррационального числа конечной дробью величину погрешности также часто удается оценить. В связи с этим вводят понятие предельной абсолютной погрешности 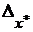, являющейся наименьшей из верхних границ 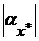, которую можно найти исходя из способа получения величины 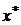. На практике часто за предельную абсолютную погрешность 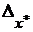принимают не наименьшую из верхних граней 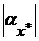, а одну из верхних граней, достаточно близкую к наименьшей. В связи с грубостью оценок точности с помощью предельных абсолютных погрешностей заметной разницы при этом не будет. Таким образом, если 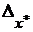= 0,003, а 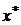= 1,12, то 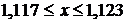(или ).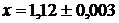

Абсолютная погрешность и предельная абсолютная погрешность могут характеризовать точность результата только при одновременном указании самого результата. В самом деле, пусть предельная абсолютная погрешность результата измерения равна 1 см. Если при этом измерялась длина комнаты, то точность удовлетворительная. Если же измерялось расстояние между двумя пунктами различных городов, то точность настолько велика, что, скорее всего, является сомнительной. Поэтому вводят еще одну характеристику точности – относительную погрешность

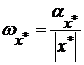. (2.2)

Точно также вводится предельная относительная погрешность

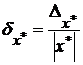. (2.3)

Относительная погрешность является величиной безразмерной и во многих случаях выражается в процентах. Часто предельные абсолютные и относительные погрешности называют просто абсолютными и относительными погрешностями.

Верные цифры числа.

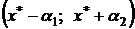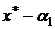При записи приближенного числа необходимо указывать соответствующую ему область неопределенности. Наиболее аккуратный способ записи будет иметь вид: , где и 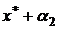– границы области неопределенности. Можно также записывать приближенное число в виде 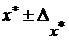. Однако оба этих способа оказываются неудобными. Поэтому в вычислительной практике часто прибегают к различным приемам, позволяющим по записи только самого приближенного числа судить о его погрешности. Один из наиболее распространенных приемов состоит в следующем.

В десятичной системе счисления числа, имеющие не более 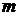разрядов, записываются единственным образом в виде

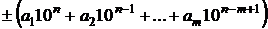, (2.4)

где 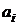– целые положительные числа 0, 1, …, 9. Например, 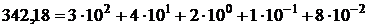. Выберем некоторое число 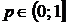. Будем в приближенном числе 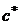, записанном в форме (4), цифру 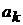считать верной, если 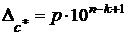( 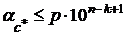). В противном случае 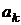считается сомнительной цифрой. Очевидно, что если 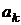является верной цифрой, то и все предыдущие цифры верные. Записывая приближенное число без указания его погрешности, требуют, чтобы все записанные цифры были верны. Так, например, если в десятичной системе будет записано приближенное число 3,14 и не будет указана его абсолютная погрешность, то это означает, что она не превышает 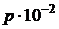. Чтобы показать, что абсолютная погрешность числа 314000 не превышает 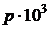, его следует записать в виде .

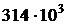Если исходное число имеет несколько сомнительных цифр, его нужно предварительно округлить. К округлениям прибегают и в том случае, когда число разрядов чрезмерно велико. В этих случаях нельзя брать 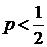, так как при этом найдутся числа, у которых последняя цифра будет оставаться сомнительной, сколько бы ни производилось округлений. Это связано с тем, что при округлении числа до 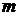старших разрядов абсолютная погрешность может возрасти на 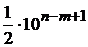. При любом выборе 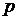найдутся такие числа, у которых последняя верная цифра после округления уже не станет верной. Наименьшим значением 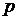, при котором после округления остается верной, по крайней мере, предпоследняя верная цифра числа является 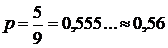. С другой стороны, чем больше берется 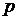, тем больше будет чисел, для которых погрешность будет завышена. Поэтому, если числа получают в результате вычислений по формулам с точными значениями исходных данных, когда можно достигнуть практически любой заданной точности, выбирают 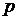возможно более близким к 0,5 (например, 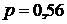или 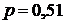и т. п.). Если же приближенные числа получаются в результате измерений или в результате вычислений с недостаточно точными исходными данными, то обычно берут .

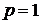Ниже будем предполагать, что 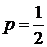. В этом случае цифра десятичного разряда числа 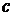приближения 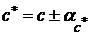будет верной, если в том же десятичном разряде чисел 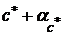и 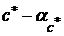стоит та же цифра. В противном случае она будет сомнительной.