Признаки сходимости положительных рядов
Если все члены ряда имеют одинаковые знаки, то ряд называется знакопостоянным. К числу таких рядов относятся ряды, все члены которых только положительные (знакоположительные, или просто положительные ряды), и ряды, все члены которых только отрицательные (знакоотрицательные ряды). Знакоотрицательные ряды можно рассматривать как частный случай положительных, у которых все члены умножены на (–1).
Положительный сходящийся ряд при перестановке членов остается сходящимся и сумма его не изменяется. Расходящийся положительный ряд при перестановке членов остается расходящимся.
Сравнение положительных рядов.
· 1-й признак сравнения. Пусть 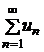 и
и 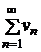 – ряды с положительными членами, причем
– ряды с положительными членами, причем 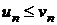 для всех номеров
для всех номеров  , начиная с некоторого. Тогда:
, начиная с некоторого. Тогда:
1) если ряд 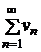 сходится, то сходится и ряд
сходится, то сходится и ряд 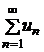 ;
;
2) если ряд 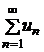 расходится, то расходится и ряд
расходится, то расходится и ряд 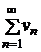 .
.
· 2-й признак сравнения (предельная форма признака сравнения). Пусть 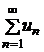 и
и 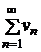 – ряды с положительными членами, причем существует конечный и отличный от нуля предел
– ряды с положительными членами, причем существует конечный и отличный от нуля предел 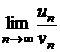 . Тогда ряды
. Тогда ряды 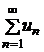 и
и 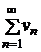 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
При использовании 1-го или 2-го признака сравнения, как правило, сравнивают исходный ряд с соответствующим рядом Дирихле. При этом часто используют эквивалентность следующих бесконечно малых последовательностей (при 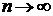 ):
):
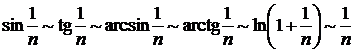 .
.
Пример. Исследовать на сходимость ряд 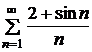 .
.
◄ Применим 1-й признак сравнения. Так как 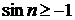 , то
, то 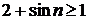 , откуда
, откуда 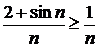 . Ряд
. Ряд 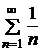 расходится, значит, расходится и больший ряд
расходится, значит, расходится и больший ряд 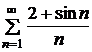 . ►
. ►
Пример. Исследовать на сходимость ряд 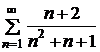 .
.
◄ Применим 2-й признак сравнения. Так как при 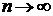 числитель дроби в общем члене ряда
числитель дроби в общем члене ряда 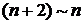 (это следует из
(это следует из 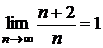 ), а знаменатель
), а знаменатель 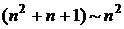 (т. к.
(т. к. 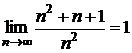 ) и, следовательно,
) и, следовательно, 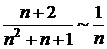 , сравним заданный ряд с гармоническим
, сравним заданный ряд с гармоническим 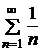 . Находим предел отношения
. Находим предел отношения 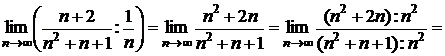 =
= 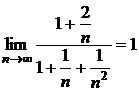 . Так как этот предел конечен и не равен нулю, а ряд
. Так как этот предел конечен и не равен нулю, а ряд 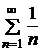 расходится, то расходится и исходный ряд. ►
расходится, то расходится и исходный ряд. ►
Пример. Исследовать на сходимость ряд 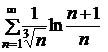 .
.
◄ Так как 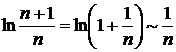 (при
(при 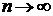 ), то
), то 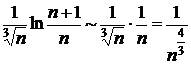 (при
(при 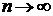 ). Ряд
). Ряд 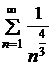 сходится (это ряд Дирихле
сходится (это ряд Дирихле 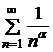 , в котором
, в котором 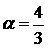 ), значит, сходится и исходный ряд. ►
), значит, сходится и исходный ряд. ►
Признак Даламбера. Пусть 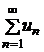 – ряд с положительными членами, и существует конечный предел
– ряд с положительными членами, и существует конечный предел 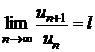 . Тогда, если
. Тогда, если 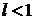 , то данный ряд сходится; если же
, то данный ряд сходится; если же 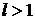 , – расходится. Если
, – расходится. Если 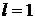 , то ряд может сходиться или расходиться; в этом случае требуется исследовать ряд с помощью других методов.
, то ряд может сходиться или расходиться; в этом случае требуется исследовать ряд с помощью других методов.
Пример. Исследовать на сходимость ряд 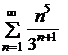 .
.
◄ Применяем признак Даламбера. Найдем предварительно отношение  :
: 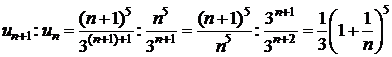 . Вычисляем предел:
. Вычисляем предел: 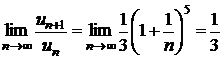 . Так как
. Так как 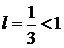 , исходный ряд сходится. ►
, исходный ряд сходится. ►
Признак Коши. Пусть 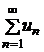 – ряд с положительными членами, и существует конечный предел
– ряд с положительными членами, и существует конечный предел 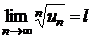 . Тогда, если
. Тогда, если 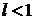 , то данный ряд сходится; если же
, то данный ряд сходится; если же 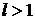 , – расходится. Если
, – расходится. Если 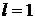 , то ряд может сходиться или расходиться; в этом случае требуется исследовать ряд с помощью других методов.
, то ряд может сходиться или расходиться; в этом случае требуется исследовать ряд с помощью других методов.
Пример. Исследовать на сходимость ряд 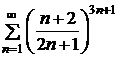 .
.
◄ Применяем признак Коши. Найдем предварительно 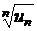 :
: 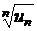 =
= 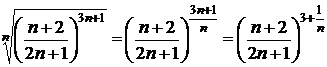 . Так как
. Так как 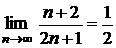 и
и 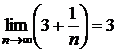 , получим
, получим 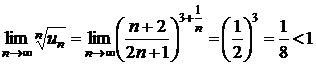 . Заданный ряд сходится по признаку Коши. ►
. Заданный ряд сходится по признаку Коши. ►
