Прямая в пространстве. Взаимное расположение плоскостей и прямых
 Система двух линейных уравнений
Система двух линейных уравнений
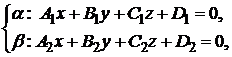 (1.3.32)
(1.3.32)
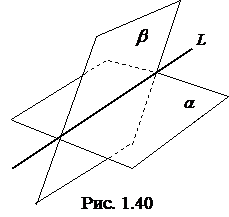
определяет прямую 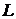 как пересечение двух плоскостей
как пересечение двух плоскостей 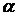 и
и 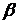 (рис. 1.40) при условии, что эти плоскости не параллельны
(рис. 1.40) при условии, что эти плоскости не параллельны 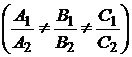 . При
. При 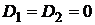 (и только в этом случае) прямая проходит через начало координат.
(и только в этом случае) прямая проходит через начало координат.
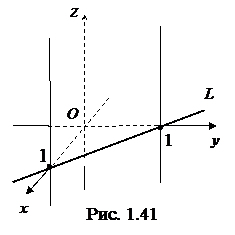
Пример. Рассмотрим систему 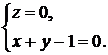 . Первое уравнение системы задает координатную плоскость
. Первое уравнение системы задает координатную плоскость 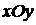 , а второе – плоскость, параллельную оси
, а второе – плоскость, параллельную оси 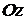 . Пересечение этих плоскостей дает прямую линию, лежащую в координатной плоскости
. Пересечение этих плоскостей дает прямую линию, лежащую в координатной плоскости 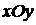 (рис. 1.41).
(рис. 1.41).
Если прямая проходит через точку 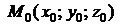 параллельно вектору
параллельно вектору 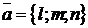 (направляющий вектор прямой), то из условия
(направляющий вектор прямой), то из условия 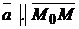 , где
, где 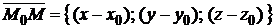 – вектор, проведенный из точки
– вектор, проведенный из точки 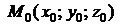 в произвольную точку прямой
в произвольную точку прямой 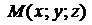 (рис. 1.42), получаем канонические уравнения прямой:
(рис. 1.42), получаем канонические уравнения прямой:
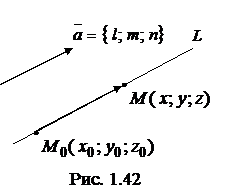
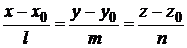 (1.3.33)
(1.3.33)
Уравнения прямой, проходящей через две точки 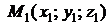 и
и 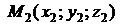 , следуют из (1.3.33), если в качестве направляющего вектора прямой взять вектор
, следуют из (1.3.33), если в качестве направляющего вектора прямой взять вектор 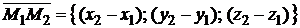 и одну из двух точек (все равно какую), через которые прямая проходит:
и одну из двух точек (все равно какую), через которые прямая проходит:
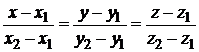 (1.3.34)
(1.3.34)
Направляющий вектор 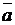 прямой, заданной как линия пересечения двух плоскостей (системой (1.3.32)), может быть получен при помощи векторного произведения нормальных векторов
прямой, заданной как линия пересечения двух плоскостей (системой (1.3.32)), может быть получен при помощи векторного произведения нормальных векторов 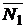 и
и 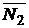 этих двух плоскостей:
этих двух плоскостей:
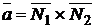 . (1.3.35)
. (1.3.35)
Обозначив в канонических уравнениях (1.3.33) отношение через 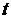 (
( 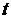 – переменный параметр), получаем параметрические уравнения прямой в пространстве:
– переменный параметр), получаем параметрические уравнения прямой в пространстве:
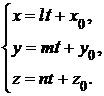 (1.3.36).
(1.3.36).
Пример. Составить параметрические уравнения прямой 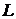 , заданной как пересечение двух плоскостей
, заданной как пересечение двух плоскостей 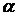 и
и 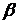 :
: 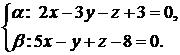 .
.
◄ Направляющий вектор прямой 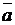 найдем по формуле (1.3.35) при
найдем по формуле (1.3.35) при 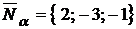 ,
, 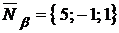 :
: 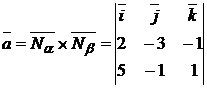 =
= 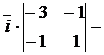
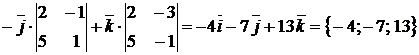 . Произвольную точку, через которую проходит прямая, можно найти, положив одну из ее координат любому значению и решив затем получающуюся из исходной системы систему двух уравнений с двумя остающимися неизвестными координатами точки. Положив
. Произвольную точку, через которую проходит прямая, можно найти, положив одну из ее координат любому значению и решив затем получающуюся из исходной системы систему двух уравнений с двумя остающимися неизвестными координатами точки. Положив 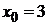 , получаем систему
, получаем систему 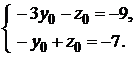 . Решение этой системы:
. Решение этой системы: 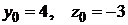 , т. е. прямая проходит через точку с координатами
, т. е. прямая проходит через точку с координатами 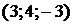 . Подставив эти координаты и координаты направляющего вектора в (1.3.36), получаем искомые уравнения прямой:
. Подставив эти координаты и координаты направляющего вектора в (1.3.36), получаем искомые уравнения прямой: 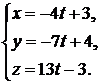 . ►
. ►
Взаимное расположение плоскостей и прямых
Угол 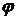 между двумя плоскостями
между двумя плоскостями 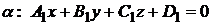 и
и 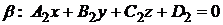 (рис. 1.43) равен углу между нормальными векторами
(рис. 1.43) равен углу между нормальными векторами 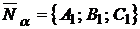 и
и 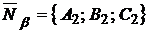 этих плоскостей, т. е.
этих плоскостей, т. е.
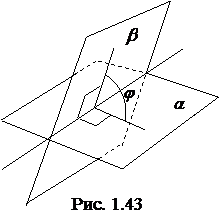
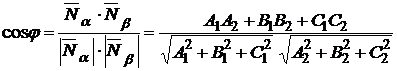 (1.3.37)
(1.3.37)
Две плоскости 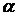 и
и 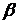 параллельны, если параллельны их нормальные векторы
параллельны, если параллельны их нормальные векторы 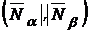 , т. е. если
, т. е. если
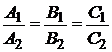 .
.
Условием перпендикулярности плоскостей является перпендикулярность их нормальных векторов: 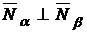 .
.
Пример. Найти угол между плоскостями 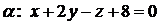 и
и 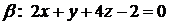 .
.
◄ Находим нормальные векторы для данных плоскостей: 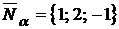 ,
, 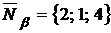 . По формуле (1.3.37) получаем
. По формуле (1.3.37) получаем 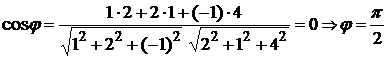 ,
,
т. е. плоскости взаимно перпендикулярны. ►
Угол 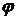 между двумя прямыми равен углу между направляющими векторами
между двумя прямыми равен углу между направляющими векторами 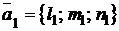 и
и 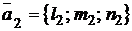 этих прямых, т. е.
этих прямых, т. е.
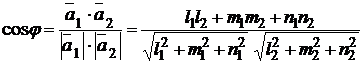 . (1.3.38)
. (1.3.38)
Прямые параллельны, если 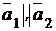 , т. е. если
, т. е. если
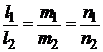 ,
,
|
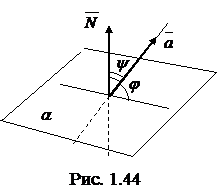
Угол  между прямой
между прямой 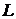 с направляющим вектором
с направляющим вектором 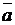 и плоскостью
и плоскостью 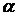 с нормальным вектором
с нормальным вектором 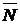 (рис. 1.44) определяется по формуле
(рис. 1.44) определяется по формуле
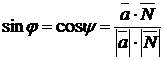 . (1.3.39)
. (1.3.39)
Пример. Найти угол между прямой 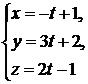 и плоскостью
и плоскостью 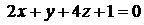 .
.
◄ По данным уравнениям находим направляющий вектор прямой 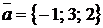 и нормальный вектор плоскости
и нормальный вектор плоскости 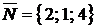 . По формуле (1.3.39) получаем
. По формуле (1.3.39) получаем 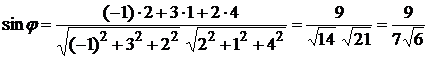 . ►
. ►
