Коэффициент ранговой корреляции Спирмена
Если потребуется установить связь между двумя признаками, значения которых в генеральной совокупности распределены не по нормальному закону, т. е. предположение о том, что двумерная выборка (xi и yi) получена из двумерной нормальной генеральной совокупности, не принимается, то можно воспользоваться коэффициентом ранговой корреляции Спирмена ( 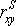 ):
):
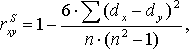
где dx и dy – ранги показателей xi и yi; n – число коррелируемых пар.
Коэффициент ранговой корреляции также имеет пределы 1 и –1. Если ранги одинаковы для всех значений xi и yi, то все разности рангов (dx - dy) = 0 и = 1. Если ранги xi и yi расположены в обратном порядке, то 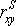 = -1. Таким образом, коэффициент ранговой корреляции является мерой совпадения рангов значений xi и yi.
= -1. Таким образом, коэффициент ранговой корреляции является мерой совпадения рангов значений xi и yi.
Когда ранги всех значений xi и yi строго совпадают или расположены в обратном порядке, между случайными величинами Х и Y существует функциональная зависимость, причем эта зависимость не обязательно линейная, как в случае с коэффициентом линейной корреляции Браве-Пирсона, а может быть любой монотонной зависимостью (т. е. постоянно возрастающей или постоянно убывающей зависимостью). Если зависимость монотонно возрастающая, то ранги значений xi и yi совпадают и 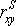 = 1; если зависимость монотонно убывающая, то ранги обратны и
= 1; если зависимость монотонно убывающая, то ранги обратны и 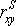 = –1. Следовательно, коэффициент ранговой корреляции является мерой любой монотонной зависимости между случайными величинами Х и Y.
= –1. Следовательно, коэффициент ранговой корреляции является мерой любой монотонной зависимости между случайными величинами Х и Y.
Из формулы видно, что для вычисления 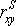 необходимо сначала проставить ранги (dx и dy) показателей xi и yi, найти разности рангов (dx - dy) для каждой пары показателей и квадраты этих разностей (dx - dy)2. Зная эти значения, находятся суммы
необходимо сначала проставить ранги (dx и dy) показателей xi и yi, найти разности рангов (dx - dy) для каждой пары показателей и квадраты этих разностей (dx - dy)2. Зная эти значения, находятся суммы 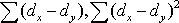 , учитывая, что
, учитывая, что 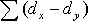 всегда равна нулю. Затем, вычислив значение
всегда равна нулю. Затем, вычислив значение 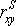 , необходимо определить достоверность найденного коэффициента корреляции, сравнив его фактическое значение с табличным. Если
, необходимо определить достоверность найденного коэффициента корреляции, сравнив его фактическое значение с табличным. Если 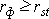 , то можно говорить о том, что между признаками наблюдается достоверная взаимосвязь. Если
, то можно говорить о том, что между признаками наблюдается достоверная взаимосвязь. Если 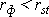 , то между признаками наблюдается недостоверная корреляционная взаимосвязь.
, то между признаками наблюдается недостоверная корреляционная взаимосвязь.
Коэффициент ранговой корреляции Спирмена вычисляется значительно проще, чем коэффициент корреляции Браве-Пирсона при одних и тех же исходных данных, поскольку при вычислении используются ранги, представляющие собой обычно целые числа.
Коэффициент ранговой корреляции целесообразно использовать в следующих случаях:
- если экспериментальные данные представляют собой точно измеренные значения признаков Х и Y и требуется быстро найти приближенную оценку коэффициента корреляции. Тогда даже в случае двумерного нормального распределения генеральной совокупности можно воспользоваться коэффициентом ранговой корреляции вместо точного коэффициента корреляции Браве-Пирсона. Вычисления будут существенно проще, а точность оценки генерального параметра р с помощью коэффициента 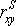 при больших объемах выборки составляет 91,2% по отношению к точности оценки по коэффициенту корреляций;
при больших объемах выборки составляет 91,2% по отношению к точности оценки по коэффициенту корреляций;
- когда значения xi и (или) yi заданы в порядковой шкале (например, оценки судей в баллах, места на соревнованиях, количественные градации качественных признаков), т. е. когда признаки не могут быть точно измерены, но их наблюдаемые значения могут быть расставлены в определенном порядке.
Пример 2. Определить достоверность взаимосвязи между показателями веса и максимального количества сгибания и разгибания рук в упоре лежа у 10 исследуемых с помощью расчета рангового коэффициента корреляции, если данные выборок таковы:
xi,кг~55; 45; 43; 47; 47; 51; 48; 60; 53;50
yi, кол-во раз ~ 26; 20; 25; 22; 27; 28; 16; 15; 18; 24
Решение
1. Расчет рангового коэффициента корреляции Спирмена произведем по формуле:
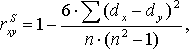
где: dx и dy — ранги показателей х и у;
n — число коррелируемых пар или исследуемых.
2 Данные тестирования занести в рабочую таблицу и сделать необходимые расчеты.
Таблица 2 – Данные тестирования
| xi | dx | yi | dy | 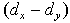 | 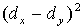 |
| -2 | |||||
| -6 | |||||
| 3.5 | -1.5 | 2.25 | |||
| 3.5 | -4.5 | 20.25 | |||
| -3 | |||||
 |  |  |  | 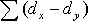 = 0 = 0 | 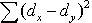 = 186,5 = 186,5 |
Тогда 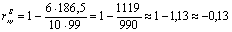
3. Сравнить расчетное значение рангового коэффициента корреляции(rф =-0,13) с табличным значением для n = 10 при α = 5% и сделать вывод.
Вывод:
1) т.к. rф = -0,13 < 0, то между данными выборок наблюдается прямая отрицательная взаимосвязь, т.е. увеличением показателей веса вызывает снижение максимального количество сгибаний и разгибаний рук в упоре лежа в группе исследуемых;
2) т.к. rф = -0,13 < rst = 0,64 для n = 10 при α = 5%, то с уверенностью Р = 95% можно говорить о том, что выявленная зависимость недостоверна.
