Понятие функции, график функции

область определения, множество значений

Зависимость переменной y от переменной х называется функцией, если каждому значению х соответствует единственное значение у. При этом используют запись: y=f(x). Переменную х называют независимой переменной (аргументом); у называют зависимой переменной (функцией). Значение у, соответствующее заданному значению х, называют значением функции.

Все значения, которые принимает независимая переменная, образуют область определения функции D(f).

Все значения, которые принимает зависимая переменная, образуют множество значений функции Е(f).

Элементы множества D(f) так же называют значениями аргумента, а соответствующие им элементы множества Е(f) - значениями функции.

Графиком функции у = f(x) называется множество всех точек (х; у) координатной плоскости, таких, что 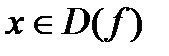, а у = f(x), причем х называется абсциссой, у – ординатой.

Для того чтобы множество точек координатной плоскости являлось графиком некоторой функции, необходимо и достаточно, чтобы любая прямая, параллельная оси Оу, пересекалась с указанным графиком не более чем в одной точке.

Способы задания функции:

1. Аналитический – с помощью формулы: у = 5х² – 7.

2. Табличный – с помощью таблицы:

х		3,5	7,3
у			1,8	9,2

3. Описательный.

4. Графический – с помощью графика:

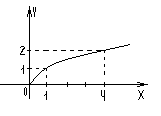
Свойства функции

1. Областью определения функции называются все значения переменной х, при которых функция имеет смысл (выполнимы указанные действия).

2. Множеством значений функции называются все значения переменной у.

3. Функция у = f(x) называется четной, если для любого значения х из области определения функции значение –х так же принадлежит области определения (область определения симметрична относительно начала отсчета) и выполняется равенство: f(-x) = f(x). График четной функции симметричен относительно оси ординат (оси Оу).

Функция у = f(x) называется нечетной, если для любого значения х из области определения функции значение -х так же принадлежит области определения и выполняется равенство: f(-x) = -f(x). График нечетной функции симметричен относительно начала координат.

4. Нулем функции называется такое значение аргумента х из области определения функции, при котором значение функции равно 0. Для того, чтобы найти нули функции необходимо решить уравнение f(x) = 0.

5. Промежутки, на которых функция либо положительна, либо отрицательна, т.е. имеет один и тот же знак, называются промежутками знакопостоянства.

6. Функция называется периодической, если существует такое число

Т ≠ 0, что для любого значения аргумента х из области определения значения х+Т и х–Т так же принадлежат области определения функции и выполняется равенство f(x) = f(x + T) = f(x - T).

7. Функция называется возрастающей на промежутке Х, если для любых х₁ и х₂ из этого промежутка, таких что х₁ < х₂, выполняется неравенство f(x₁) < f(x₂), т.е. большему значению аргумента соответствует большее значение функции.

Функция называется убывающей на промежутке Х, если для любых х₁ и х₂ из этого промежутка, таких что х₁ < х₂, выполняется неравенство

f(x₁) > f(x₂), т.е. большему значению аргумента соответствует меньшее значение функции.

Возрастающая или убывающая на некотором промежутке функция называется монотонной.

Промежутки, на которых функциявозрастает или убывает, называются промежутками монотонности.

8. Функция называется ограниченной снизу на некотором множестве Х, если существует такое действительное число М, что для каждого 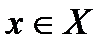, f(x) 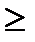M.

Функция называется ограниченной сверху на некотором множестве Х, если существует такое действительное число М, что для каждого 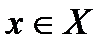, f(x) 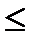M.

Функция называется ограниченной на некотором множестве Х, если она ограничена и снизу, и сверху.

9. Наибольшим значением функции называется самое большое значение, которое принимает переменная у; наименьшим значением функции называется самое маленькое значение, которое принимает переменная у.