Определение двойственной задачи к общей задаче

Линейного программирования

Вернемся к общей задаче линейного программирования:

f(X) = c₁x₁ + c₂x₂ + … + c_nx_n ® max, (4.7)

a₁₁x₁ + a₁₂x₂ + a₁₃x₃ + … + a_1nx_n £ b₁,

…………………………………………

a_k1x₁ + a_k2x₂ + a_k3x₃ + … + a_knx_n £ b_k,

a_k+1;1 x₁ + a_k+1;2 x₂ + … + a_k+1;n x_n = b_k+1, (4.8)

………………………………………….

a_m1x₁ + a_m2x₂ + a_m3x₃ + … + a_mnx_n = b_m,

x₁, x₂, x₃, …, x_s ³ 0.

Без ограничения общности мы будем как и раньше предполагать, что исходная задача является задачей на максимум. Первые k ограничений являются неравенствами вида £, остальные n – k ограничений являются равенствами, и первые s переменных ограничены на знак.

Двойственной задачей к задаче (4.7) – (4.8) называется задача

j(Y) = b₁y₁ + b₂y₂ + … + b_my_m ® min, (4.9)

a₁₁y₁ + a₂₁y₂ + a₃₁y₃ + … + a_m1y_m ³ c₁,

…………………………………………

a_1sx₁ + a_2sy₂ + a_3sy₃ + … + a_msy_m ³ c_s,

a_1;s+1 y₁ + a_{2; s+1} y₂ + … + a_{m; s+1} y_m = c_s+1, (4.10)

………………………………………….

a_1nx₁ + a_2ny₂ + a_3ny₃ + … + a_mny_m = c_n,

y₁, y₂, y₃, …, y_k ³ 0.

Количество ограничений двойственной задачи совпадает с числом переменных исходной задачи, а число переменных двойственной задачи совпадает с количеством ограничений исходной задачи. Тем самым устанавливается соответствие между ограничениями и переменными взаимно двойственных задач (несколько позднее мы докажем, что задача, двойственная к двойственной задаче, совпадает с исходной).

Двойственная задача (4.9) – (4.10) строится по следующему правилу:

1. Пусть исходная задача является задачей на максимум с ограничениями, являющимися равенствами, или неравенствами вида £. Тогда двойственная задача является задачей на минимум с ограничениями, являющимися равенствами, или неравенствами вида ³.

2. Коэффициенты функции цели (4.9) являются правыми частями системы ограничений (4.8) исходной задачи.

3. Правые части системы ограничений (4.10) двойственной задачи совпадают с коэффициентами функции цели (4.7) исходной задачи.

4. Матрица системы ограничений (4.10) является транспонированной матрицей системы (4.8).

5. Те ограничения двойственной задачи, которые соответствуют ограниченным на знак переменным исходной задачи, имеют вид неравенств вида ³. Остальные ограничения двойственной задачи являются равенствами.

6. Те переменные двойственной задачи, которые соответствуют ограничениям исходной задачи вида £, ограничены на знак. Остальные переменные двойственной задачи ограничений на знак не имеют.

Теорема 5.1. Задача, двойственная к задаче (4.9) – (4.10), совпадает с исходной задачей (4.7) – (4.8).

Доказательство. Переформулируем задачу (4.9) – (4.10), превратив ее в задачу на максимум с ограничениями, являющимися равенствами или неравенствами вида £. Для этого умножим все ограничения (4.10) на (–1), и рассмотрим новую функцию цели 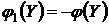. При этом 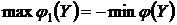. Таким образом, мы приходим к следующей задаче:

j₁(Y) = – b₁y₁ – b₂y₂ – … – b_my_m ® max, (4.11)

– a₁₁y₁ – a₂₁y₂ – a₃₁y₃ – … – a_m1y_m ³ – c₁,

……………………………………………

– a_1sx₁ – a_2sy₂ – a_3sy₃ – … – a_msy_m ³ – c_s,

– a_1;s+1 y₁ – a_{2; s+1} y₂ – … – a_{m; s+1} y_m = – c_s+1, (4.12)

…………………………………………….

– a_1nx₁ – a_2ny₂ – a_3ny₃ – … – a_mny_m = – c_n,

y₁, y₂, y₃, …, y_k ³ 0.

Составим двойственную задачу к задаче (4.11) – (4.12), обозначив двойственные переменные через x_i, а функцию цели через f₁(X):

f₁(X) = – c₁x₁ – c₂x₂ – … – c_nx_n ® min, (4.13)

– a₁₁x₁ – a₁₂x₂ – a₁₃x₃ – … – a_1nx_n £ – b₁,

………………………………….….………

– a_k1x₁ – a_k2x₂ – a_k3x₃ – … – a_knx_n £ – b_k,

– a_k+1;1 x₁ – a_k+1;2 x₂ – … – a_k+1;n x_n = – b_k+1, (4.14)

……………………………….…………….

–a_m1x₁ – a_m2x₂ – a_m3x₃ – … – a_mnx_n = – b_m,

x₁, x₂, x₃, …, x_s ³ 0.

Очевидно, что 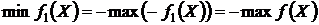. Следовательно, умножая функцию цели и ограничения задачи (4.13) – (4.14) на (–1), мы получаем исходную задачу (4.7) – (4.8). Ч.т.д.

При решении различных экономических задач мы зачастую сталкиваемся с необходимостью решать сразу две взаимно-двойственные задачи.

Так, взаимно двойственными являются задачи об использовании сырья или его продажи [3]. В теории игр взаимно двойственные задачи решают конкурирующие стороны.

Оказывается, решение задачи, двойственной к исходной, можно искать методом Штифеля параллельно с решением основной задачи. При этом используются одни и те же жордановы таблицы. Необходимо только в жорданову таблицу ввести один дополнительный заглавный столбец и одну дополнительную заглавную строку. При одном шаге метода Штифеля основная задача преобразуется с помощью модифицированных жордановых исключений. При этом двойственная задача преобразуется методом обыкновенных жордановых исключений. Подробнее о таком методе решения взаимно-двойственных задач можно прочитать в [2].

В частности, таким способом доказаны следующие теоремы двойственности (мы их приводим без доказательства):

Теорема 5.2. Если одна из двойственных задач имеет оптимальное решение, то и другая его имеет, причем экстремальные значения их функций цели совпадают:

.

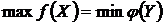Если же в одной задаче функция цели не ограничена, то двойственная ей задача не имеет планов.

Теорема 5.3 (теорема о равновесии). Если оптимальное решение задачи обращает какое-то ее ограничение в строгое неравенство, то в оптимальном плане двойственной задачи соответствующая переменная равна нулю. Если же какая-то компонента оптимального плана положительна, то соответствующее ограничение двойственной задачи ее оптимальным планом обращается в строгое неравенство.

Решение двойственной задачи

В данном параграфе мы рассмотрим пример решения двойственной задачи, основанный на теореме о равновесии (теорема 5.3).

Пример 4.2. 1. Решить общую задачу линейного программирования.
2. Составить и решить двойственную задачу, используя теорему о равновесии.

z(X) = – 5x₁ + 3x₂ + 5x₃ – 7x₄ ® max, (4.15)

2x₁ + x₂ + x₃ + 3x₄ ³ – 3,

2x₁ + 3x₂ + 4x₃ + 2x₄ £ 3, (4.16)

– x₁ + 2x₂ + 2x₃ – x₄ = 4,

x₂, x₃, x₄ ³ 0.

Решение. Для удобства составления двойственной задачи и решения основной задачи добьемся того, чтобы все ограничения задачи на максимум были равенствами или неравенствами вида £ . Для этого умножим первое неравенство системы (4.16) на – 1. Мы приходим к задаче:

z(X) = – 5x₁ + 3x₂ + 5x₃ – 7x₄ ® max, (4.17)

– 2x₁ – x₂ – x₃ – 3x₄ £ 3,

2x₁ + 3x₂ + 4x₃ + 2x₄ £ 3, (4.18)

– x₁ + 2x₂ + 2x₃ – x₄ = 4,

x₂, x₃, x₄ ³ 0.

1. Для решения задачи (4.17) – (4.18) методом Штифеля введем в первое и во второе ограничения системы (4.18) добавочные переменные y₁³ 0 и y₂³ 0.

y₁ = 2x₁ + x₂ + x₃ + 3x₄ + 3,

y₂ = – 2x₁ – 3x₂ – 4x₃ – 2x₄ + 3, (4.19)

0 = x₁ – 2x₂ – 2x₃ + x₄ + 4,

y₁, y₂, x₂, x₃, x₄ ³ 0.

Таким образом, задачу (4.17), (4.19) можно записать в виде жордановой таблицы 4.12:

	–x1	–x2	–x3	–x4				–x2	–x3	–x4
y1	–2	–1	–1	–3			y1	–5	–5	–1	–5
y2							y2
	–1			–1			x1	–2	–2		–4
z		–3	–5				z

Табл. 4.12. Табл. 4.13.

Заметим, что числа, составляющие первые три строки таблицы 4.12, совпадают с числами, образующими основную матрицу системы (4.18). Последняя строка таблицы состоит из коэффициентов функции цели (4.18), взятых с противоположным знаком. Таким образом, первоначальная жорданова таблица мола быть составлена сразу из условия исходной задачи (4.17) – (4.18).

На первом шаге метода Штифеля выберем в качестве разрешающего элемента элемент а₃₁ = – 1. При этом неограниченная на знак свободная переменная x₁ меняется с базисной переменной 0. После первого шага из таблицы можно вычеркнуть столбец, верхний заглавный элемент которого равен нулю (первый столбец). Строку, соответствующую неограниченной на знак переменной x₁, можно, предварительно запомнив, исключить из таблицы.

После первого шага мы приходим к таблице 4.13. В крайнем правом столбце таблицы 4.13 имеется отрицательное число а₁₄ = – 5. Следовательно, базисное решение, соответствующее данной таблице, не является опорным планом задачи (4.17), (4.19). Для того чтобы попытаться войти в область планов задачи, нужно найти в первой строке таблицы 4.13 отрицательное число (например, а₁₃ = – 1) и выбрать разрешающий элемент в столбце, содержащем данный отрицательный элемент (в данном случае – это третий столбец).

Разрешающий элемент в третьем столбце выбираем по принципу минимального симплексного отношения. В данном случае минимальное симплексное отношение соответствует как раз элементу а₁₃ = – 1. Дело в том, для второго оставшегося элемента а₂₃ = 0 симплексное отношение вообще не определено. Выбирая в таблице 4.13 в качестве разрешающего элемента а₁₃ = – 1, после одного шага метода Штифеля, мы приходим к таблице 4.14:

	–x2	–x3	–y1		ti2			–x2	–x4	–y1
x4			–1				x3		1/5	–1/5
y2					11/8		y2	–1	–8/5	8/5
z	–3	–5					z

Табл. 4.14. Табл. 4.15.

Из таблицы 4.14 видно, что соответствующее ей базисное решение уже является опорным планом задачи (т.к. свободные члены b₁ = 5 и
b₂ = 11 не являются отрицательными числами). Но наличие отрицательных оценок свободных переменных говорит о том, что данный опорный план не является оптимальным. Сделаем еще один шаг метода Штифеля. Выберем для поиска разрешающего элемента второй столбец, соответствующий наименьшей отрицательной оценке – 5.

Для чисел а₁₂ = 5 и а₂₂ = 8 вычислим симплексные отношения и запишем их в правый дополнительный столбец таблицы 4.14:

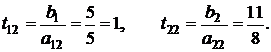
Минимальное симплексное отношение приходится на первую строку. Поэтому в качестве разрешающего элемента нужно выбрать элемент а₁₂ = 5. После пересчета мы приходим к таблице 4.15. Все оценки свободных переменных в таблице 4.15 строго больше нуля. Следовательно, мы получили оптимальный опорный план, и этот план является единственным.

Некоторые компоненты оптимального плана 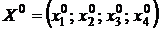и добавочные переменные y₁ и y₂ находятся из таблицы 4.15.

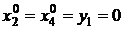как свободные переменные.

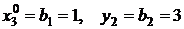– значения базисных переменных.

При этом максимум функции цели находится в правом нижнем углу таблицы:

.

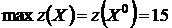Значение переменной 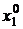найдем из запомненной ранее третьей строки таблицы 4.13:

.

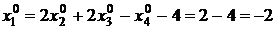Таким образом, мы нашли решение исходной задачи (4.15) – (4.16):

.

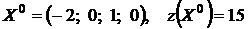2. Составим задачу, двойственную к исходной задаче (4.17) – (4.18). Мы получим следующую задачу на минимум:

g(Y) = 3y₁ + 3y₂ + 4y₃ ® min, (4.20)

– 2y₁ + 2y₂ – y₃ = – 5,

– y₁ + 3y₂ + 2y₃ ³ 3,

– y₁ + 4y₂ + 2y₃ ³ 5, (4.21)

– 3y₁ + 2y₂ – y₃ ³ – 7,

y₁, y₂ ³ 0.

Обозначим через 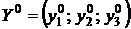– оптимальный опорный план двойственной задачи (4.20) – (4.21) воспользуемся теоремой о равновесии.

1. Подставим координаты оптимального опорного плана 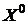в систему ограничений (4.18):

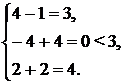
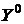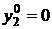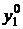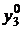Так как второе ограничение превратилось в строгое неравенство, то соответствующая компонента оптимального опорного плана двойственной задачи равна нулю ( ). Осталось найти компоненты и . Для этого воспользуемся второй частью теоремы о равновесии.

2. Так как третья компонента оптимального опорного плана 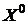строго больше нуля ( 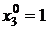), то соответствующее (третье) ограничение двойственной задачи, при подстановке в него компонент оптимального плана 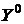, обратится в равенство. Данное равенство вместе с первым ограничением (которое само по себе является равенством) дают нам систему линейных уравнений для нахождения 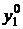и :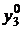

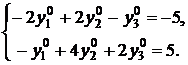(4.22)

Подставляя в систему (4.22) уже найденное значение 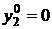, получим систему двух уравнений с двумя неизвестными:

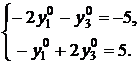(4.23)

Решением данной системы является 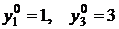. Таким образом, мы нашли оптимальный опорный план двойственной задачи: 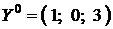. При этом экстремальные значения функций цели взаимно-двойственных задач совпадают:

.

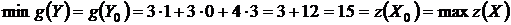ПРИЛОЖЕНИЯ

Контрольное задание №1. Вычислить ранг матрицы.

1. 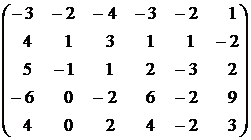.	2. .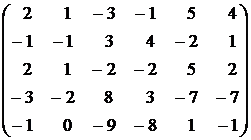
3. 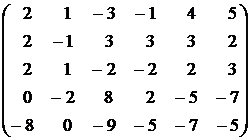.	4. .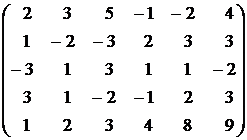
5. 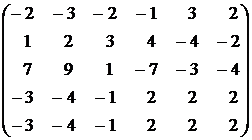.	6. .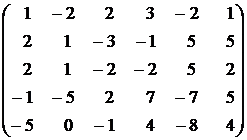
7. 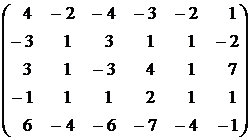.	8. .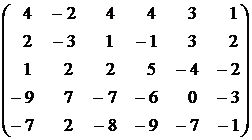
9. 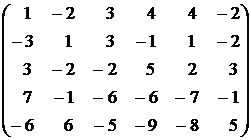.	10. .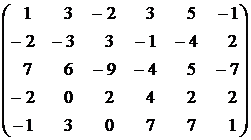
11. 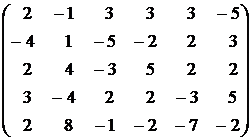.	12. .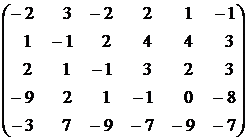
13. 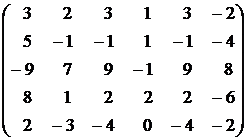.	14. .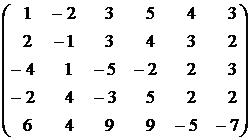
15. 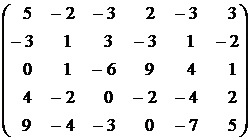.	16. .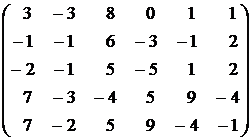
17. 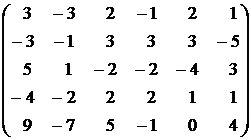.	18. .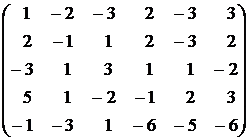
19. 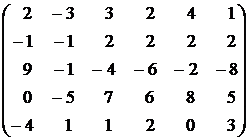.	20. .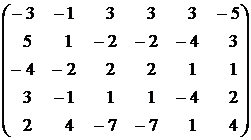

Контрольное задание №2. Найти общее решение системы линейных уравнений.

1.	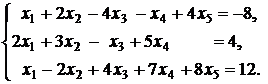2.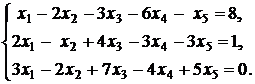
3.	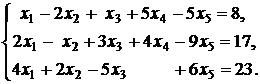4.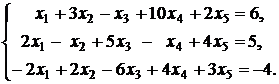
5.	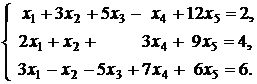6.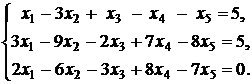
7.	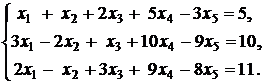8.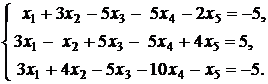
9.	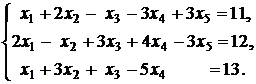10.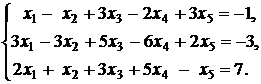
11.	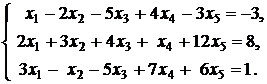12.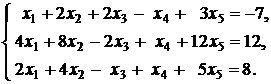
13.	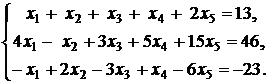14.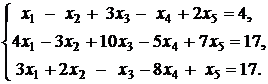
15.	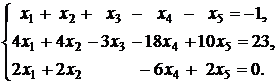16.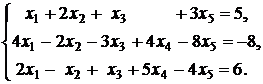
17.
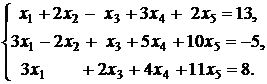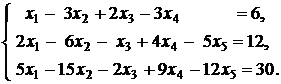18.	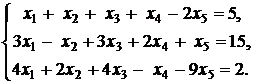19.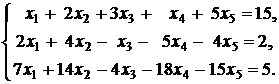

Контрольное задание №3. Дана общая задача линейного программирования. Требуется: 1) решить задачу методом Штифеля; 2) составить и решить двойственную задачу, используя теорему о равновесии.

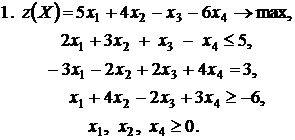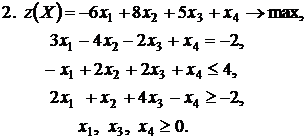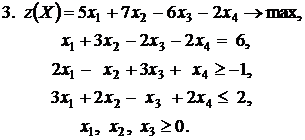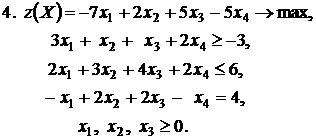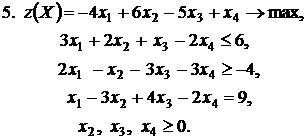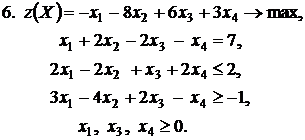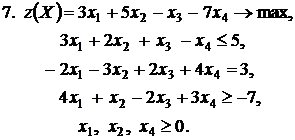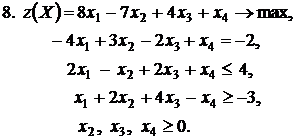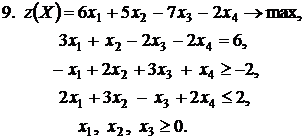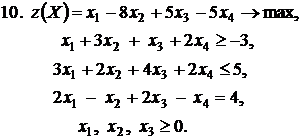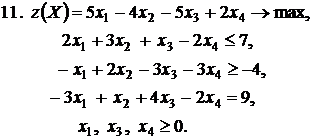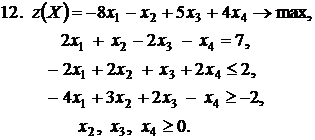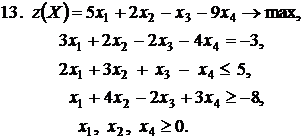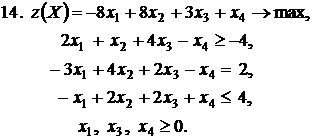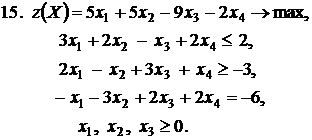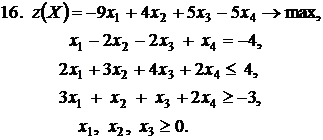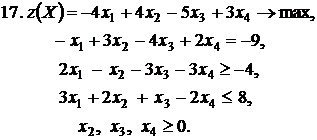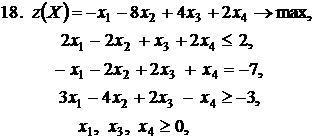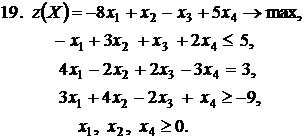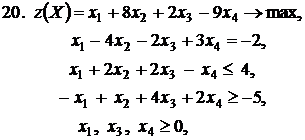ЛИТЕРАТУРА

Основная

1. Замбицкий Д.К. Линейная алгебра и линейное программирование: Учеб. пособие / Д.К. Замбицкий, М.К. Замбицкий. – Кишинэу: Еврика, 1997. – 200 с.

2. Зуховицкий С. И. Линейное и нелинейное программирование / С. И. Зуховицкий, Л.И. Авдеева. – М.: Наука, 1967. – 352 с.

3. Полунин И.Ф. Курс математического программирования / И.Ф. Полунин. – Минск: Вышэйш. шк., 1968. – 253 с.

4. Полунин И.Ф. Курс математического программирования: Для с.-х. вузов по спец. «Экономика и организация сельского хоз-ва», «Бухгалтерский учет в сельском хоз-ве» и «Экономика и организация водного хоз-ва» / И.Ф. Полунин. – 3-е изд., доп. – Минск: Вышэйш. шк., 1975. –
380 с.

5. Полунин И.Ф. Курс математического программирования : Для с.-х. вузов по спец. «Экономика и организация сельского хоз-ва» и «Бухгалтерский учет в сельском хоз-ве» / И.Ф. Полунин. – Минск: Вышэйш. шк., 1970. – 318 с.

Дополнительная

1. Зуховицкий С. И. Линейное и выпуклое программирование / С.И. Зуховицкий, Л.И. Авдеева. – 2-е, изд. переработ. и доп. – М.: Наука, 1967. – 360 с.

2. Полунин И.Ф. Математическое программирование в землеустройстве: Учеб. пособие для землеустроит. фак. с.-х. вузов / И.Ф. Полунин. – Минск: Вышэйш. шк., 1968. – 253 с.

3. Еремин И.И. Теория линейной оптимизации / И.И. Еремин; Отв. ред. Л.Д. Попов; РАН. УРО. Ин-т математики и механики. – Екатеринбург, 1999. – 312 с.

Составитель ст. преп. Уксусов Сергей Николаевич

Редактор Тихомирова О.А.