Метод модифицированных жордановых исключений
Данный метод аналогичен методу обыкновенных жордановых исключений. Только независимые переменные записывают в верхнюю заглавную строку жордановой таблицы с противоположным знаком. При этом несколько изменяется алгоритм пересчета коэффициентов системы. Пусть, по-прежнему, дана система линейных равенств:
a11x1 + a12x2 +…+ a1jxj + … + a1sxs + … + a1nxn + y1 = 0,
……………………………………………………………...
ai1x1 + ai2x2 +…+ aijxj + …+ aisxs + … + ainxn + yi = 0,
………………………………………………………………
ar1 x1 + ar2 x2 + …+ arjxj +… + arsxs + … + arn xn + yr = 0, (1.6)
………………………………………………………………
am1x1 + am2x2 +…+ amjxj + … + amsxs + …+ amnxn + ym = 0.
Перенесем все слагаемые, содержащие xj в правую часть равенств. Получим систему:
y1 = a11(–x1) + a12(–x2) +…+ a1j(–xj) + … + a1s(–xs) + … + a1n(–xn),
…………………………………………………………………..……....
yi = ai1(–x1) + ai2(–x2) +…+ aij(–xj) + …+ ais(–xs) + … + ain(–xn),
………………………………………………………………………..…
yr = ar1(–x1) + ar2(–x2) + …+ arj(–xj) +… + ars(–xs) + … + arn(–xn), (1.7)
………………………………………………….…………………….…
ym = am1(–x1)1 + am2(–x2) +…+ amj(–xj) + … + ams(–xs) + …+ amn(–xn).
Из произвольного (r-го) равенства выразим произвольную переменную xs, и подставим во все остальные равенства. Коэффициент ars при
(–xs) должен быть отличен от нуля. Число ars по-прежнему называется разрешающим элементом. Мы получим следующую систему:
y1 = b11(–x1) + b12(–x2) +…+ b1j(–xj) + … + b1s(–yr) + … + b1n(–xn),
………………………………………………………………..………....
yi = bi1(–x1) + bi2(–x2) +…+ bij(–xj) + …+ bis(–yr) + … + bin(–xn),
………………………………………………………………………..…
xs = br1(–x1) + br2(–x2) + …+ brj(–xj) +… + brs(–yr) + … + brn(–xn), (1.8)
…………………………………………………………………..………
ym = bm1(–x1)1 + bm2(–x2) +…+ bmj(–xj) + … + bms(–yr) + …+ bmn(–xn).
Вычислим коэффициенты полученной системы (1.8) через коэффициенты исходной системы (1.7). Начнем с r-го уравнения, которое после выражения переменной xs через остальные переменные, примет вид:
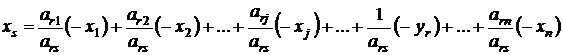(1.9)
Таким образом, новые коэффициенты r-го уравнения вычисляются по следующим формулам:
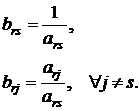(1.10)
Вычислим теперь новые коэффициенты bij произвольного уравнения (i ¹ r). Для этого подставим выраженную в (1.3) переменную xs в i-е уравнение системы (1.1):
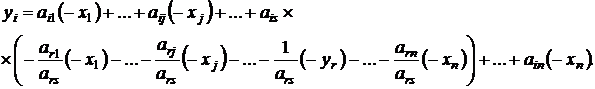
После приведения подобных членов получим:
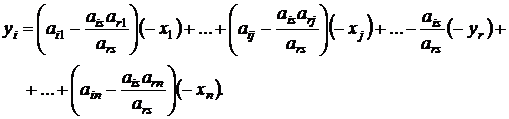(1.11)
Из равенства (1.11) получим формулы, по которым вычисляются коэффициенты системы произвольного уравнения системы (1.8), за исключением r-го уравнения:
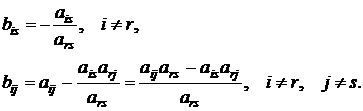(1.12)
Преобразования систем линейных уравнений методом модифицированных жордановых исключений оформляется в виде таблиц, аналогичных таблицам метода обыкновенных жордановых исключений. Только переменные, находящиеся в верхней заглавной строке таблицы, берутся со знаком минус. Таким образом, задаче (1.7) ставится в соответствие следующая жорданова таблица:
| –x1 | –x2 | … | –xj | … | –xs | … | –xn | |
| y1 | a11 | a12 | a1j | a1s | a1n | |||
| ………………………………………………………………….. | ||||||||
| yi | ai1 | ai2 | aij | ais | ain | |||
| ………………………………………………………………….. | ||||||||
| yr | ar1 | ar2 | arj | ars | arn | |||
| …………………………………………………………………. | ||||||||
| yn | am1 | am2 | amj | ams | amn |
Табл. 1.5.
После совершения одного шага, в результате которого независимая переменная xs заменяется переменной yr, мы приходим к следующей таблице:
| –x1 | –x2 | … | –xj | … | –yr | … | –xn | |
| y1 | b11 | b12 | b1j | b1s | b1n | |||
| ………………………………………………………………….. | ||||||||
| yi | bi1 | bi2 | bij | bis | bin | |||
| ………………………………………………………………….. | ||||||||
| xs | br1 | br2 | brj | brs | brn | |||
| …………………………………………………………………. | ||||||||
| yn | bm1 | bm2 | bmj | bms | bmn |
Табл. 1.6.
Заметим, что в левый заглавный столбец переменная xs попадает со знаком плюс, а в верхнюю заглавную строку переменная yr попадает со знаком минус. Разрешающий элемент ars мы по-прежнему будем выделять жирным шрифтом.
Алгоритм пересчета коэффициентов при переходе от таблицы (1.5) к таблице (1.6), вытекающий из формул (1.10) и (1.12), почти не отличается от соответствующего алгоритма метода обыкновенных жордановых исключений. Отличие состоит только в изменении знаков пересчитываемых коэффициентов разрешающей строки и разрешающего столбца:
1. Разрешающий элемент заменяется обратным числом: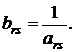 
2. Остальные элементы разрешающей строки делятся на разрешающий элемент: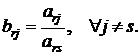 
3. Остальные элементы разрешающего столбца делятся на разрешающий элемент и меняют знак на противоположный: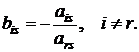 
4. Элементы, не попавшие в разрешающую строку и разрешающий столбец, пересчитываются по формулам: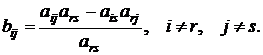 
Последнюю формулу, так же как и раньше, можно запоминать, используя диаграмму:
| aij | ais | ||
| + | – | ||
| arj | ars |
Пример 1.2. Пусть дана система линейных равенств:
y1 = 3x1 – 2x2 – 4x3 + 2x4,
y2 = 3x1 – 9x2 + 2x3 – 8x4,
y3 = –3x1 + 7x2 – 5x3 + 6x4.
Применяя метод модифицированных жордановых исключений, запишем данную систему в виде следующей жордановой таблицы:
| –x1 | –x2 | –x3 | –x4 | |
| y1 | –3 | –2 | ||
| y2 | –3 | –2 | ||
| y3 | –7 | –6 |
Табл. 1.7.
Выберем в качестве разрешающего элемента число –2, находящееся на пересечении 2-ой строки и 3-го столбца. При этом переменная x3 меняется с переменной y2 местами, и мы получим новую таблицу:
| –x1 | –x2 | –y2 | –x4 | |
| y1 | -9 | |||
| x3 | 1,5 | –4,5 | –0,5 | –4 |
| y3 | –4,5 | 15,5 | 2,5 |
Табл. 1.8.
Элементы таблицы 1.8 вычислялись по описанному выше алгоритму:
1. Разрешающий элемент заменился на обратное число:
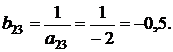
2. Остальные элементы разрешающей строки вычислялись по формуле:
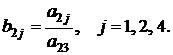
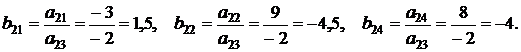
3. Остальные элементы разрешающего столбца вычислялись по формуле:
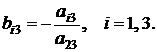
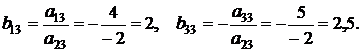
4. Остальные коэффициенты системы пересчитывались по формулам:
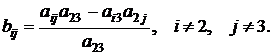
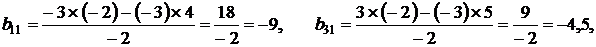
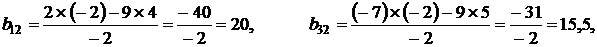
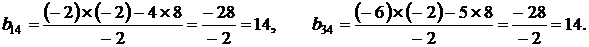
В заключение первой главы отметим, что, несмотря на похожесть двух описанных выше методов, оба они находят свое применение в различных разделах математики. Так, в линейной алгебре гораздо чаще используется метод обыкновенных жордановых исключений как менее громоздкий по сравнению с методом модифицированных жордановых исключений. Метод модифицированных жордановых исключений был специально разработан для решения задач математического программирования. Дело в том, что метод модифицированных жордановых исключений обладает одним замечательным свойством: на каждом шаге элементы разрешающего столбца меняют свои знаки, а разрешающей строки – нет (за исключением разрешающего элемента). На использовании этого свойства и построен так называемый метод Штифеля, описанный в третьей главе настоящего пособия.
ГЛАВА II
ПРИМЕНЕНИЕ МЕТОДА ЖОРДАНОВЫХ ИСКЛЮЧЕНИЙ
В ЛИНЕЙНОЙ АЛГЕБРЕ