Доверительный интервал для значений зависимой переменной

Ошибка регрессионного прогноза составляет:

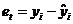, (40)

где 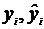- соответственно действительное и предсказанное значения зависимой переменной.

Поскольку

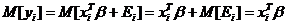
и согласно (10), (11)

,

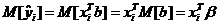где 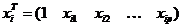- вектор – строка, представляющий собой
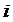-ю строку ( 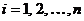) матрицы 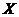объясняющих переменных, ошибка (40) имеет нулевое математическое ожидание .

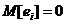Дисперсия ошибки представляется выражением:

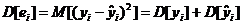(41)

В силу того, что второе слагаемое в правой части (41) с учётом можно представить в виде:

,

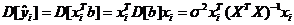а первое слагаемое равно

,

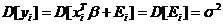их сумма, представляющая собой величину среднеквадратической ошибки интервального прогноза значений результирующего показателя для некоторого набора значений 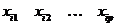, определяется выражением:

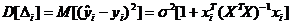(42)

В итоге посредством замены в (42) неизвестного значения 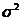на её оценку 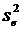получается несмещенная оценка дисперсии индивидуальных значений независимой переменной 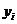, соответствующих значениям предикторов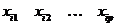

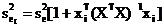(43)

Доверительный интервал для находится по формуле:

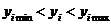, (44)

где 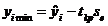, , 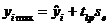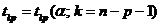- критическая точка распределения Стьюдента с 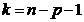степенями свободы для уровня значимости .

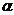Пример оформления лабораторной работы

Задача

Имеются данные о величинах объёма реализации продукции у_i фирмы (i-порядковый номер вида продукции), которые зависят от цены каждого вида продукции и расходов на рекламу.

Таблица 10

i

yi

xi1

xi2

Требуется

1. Построить выборочное уравнение линейной множественной регрессии (найти вектор коэффициентов b).

2. Рассчитать общую сумму квадратов Q, сумму квадратов, объяснён­ную регрессией Q_r, остаточную сумму квадратов Q_e, несмещённые оценки соответствующих дисперсий s², s_r², s_e² и средних квадратических отклонений s, s_r, s_e. Найти стандартные отклонения коэффициентов регрессии s_bj. С дове­рительной вероятностью g =0,95 оценить значимость коэффициентов рег­рессии и для значимых коэффициентов определить доверительные интер­валы.

3. Рассчитать выборочный множественный коэффициент детерминации 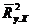, используя общую формулу и выражение через определители соответст­вующих матриц выборочных парных коэффициентов корреляции, и найти значение скорректированного коэффициента .

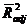4. С доверительной вероятностью g =0,95 оценить значимость уравне­ния регрессии и найти доверительные интервалы для отдельных значений y_i.

Решение

1. Для определения параметров выборочного уравнения линейной регрессии строим расчётную таблицу (табл. 11, столбцы 1-4).

а) находим выборочные коэффициенты уравнения регрессии по формуле (8). Для этого:

- записываем матрицу Х_15×3 объясняющих переменных, в которой первый столбец состоит из единиц (он соответствует умножению коэффициента b₀ на единицу):

X = ;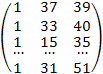

- записываем транспонированную матрицу Х^Т

Х^Т = ;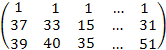

- находим произведение матриц Х^ТХ, используя Мастер функций –Математические– МУМНОЖ,вводя в массив 1 ниспадающего окна матрицу Х, а в массив 2 – матрицу Х^Т, предварительно выделив массив размером 3 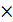3 для результата:

Х^ТХ = ;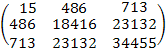

- аналогично вычисляем произведение матриц:

Х^Ту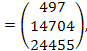

Где у= ;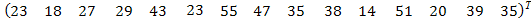

- находим обратную матрицу (Х^Т 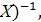используя Мастер функций –Математические– МОБР:

(Х^Т = ;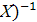

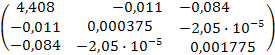- определяем вектор bвыборочных оценок коэффициентов с помощью команд Мастер функций –Математические– МУМНОЖ:

b= (Х^Т 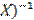Х^Ту = .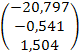

b) записываем выборочное уравнение линейной множественной регрессии:

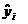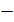= 20, 797 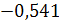х_i1 + 1,504х_i2.

2. Для выполнения задания 2

a) заполняем столбцы 6-8 таблицы 11 и суммируем полученные элементы каждого из них, в результате находим[1]:

Q = 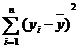= 2179,73; s² = 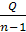= 155,695; s = 12,48;

Q_r = 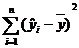= 2006,56; s_r² = 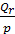= 1003,28; s_r = 31,68;

Q_e = 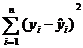= 173,18; s_e² = 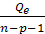= 14,43; s_e = 3,799.

b) далее находим вектор несмещённых оценок дисперсии и вектор стандартных отклонений коэффициентов регрессии, предварительно сформировав вспомогательный вектор из диагональных элементов [(Х^ТХ)^-1]_jj матрицы (Х^ТХ)^-1, по формуле (15):

s_b² = s_e² [(Х^ТХ)^-1]_jj = ,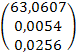

s_{b =} s_e = .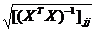

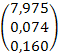Итак, стандартные отклонения равны соответственно 7,98 – для b₀,
0,07 – для b₁, 0,16 – для b₂. Поскольку они существенно меньше значений оценок коэффициентов регрессии, то можно сделать вывод, что коэффициенты регрессии значимы.

c) учитывая (20), значение g = 0,95, уровень значимости α= 0,05 нахо­дим t_кр=2,179с помощью стандартной статистической функции СТЬЮД­РАСПОБР( 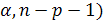, n =15, p =2, при этом вектор t-статистик 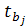= 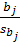критерия значимости коэффициентов регрессии определяется так:

t_b = = .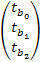

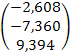Коэффициенты b₀ , b₁ и b₂ значимы, т.к. 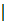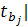> t_кр на заданном уровне значимости.

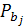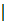
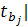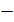d) вычисляем вектор P-значений для коэффициентов с помощью функции СТЬЮДРАСП ( ; n p 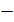1; 2):

Р_b= .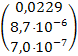

Очевидно, 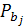< α, т.е. вывод о значимости всех коэффициентов регрессий подтверждается.

e) определим доверительные интервалы для коэффициентов регрессии, учитывая, что истинное значение β_i коэффициента регрессии лежит в интервале β_{i min} < β_i < β_{i max}:

β_min = b 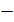t_кр s_b= ;

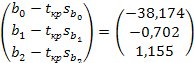β_max = b 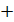t_кр s_b= .

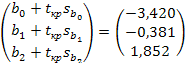3. Рассчитываем значения выборочных множественных коэффициентов детерминации и корреляции.

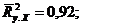а) по формуле (25):

Величина коэффициента детерминации показывает, что 92% вариации зависимой переменной обусловлены влиянием включенных факторов, а остальные 8% - влиянием случайных факторов.

b) вычислим коэффициент детерминации по формуле (26). Для этого запишем матрицу парной корреляции (ее элементы определяются с помощью статистической функции КОРРЕЛ с аргументами у, x_j, x_k, j=1,2; k=1,2:

R_уХ = = .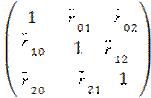

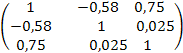с) запишем матрицу межфакторной парной корреляции (из матрицы R_уХ):

R_ХХ =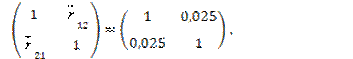

Используя математическую функцию МОПРЕД с соответствующими массивами R_уХ, R_ХХ, вычисляем det R_уХ и det R_ХХ. Тогда

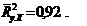
d) вычисляем скорректированный коэффициент детерминации согласно формуле (34):

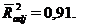
4. Рассчитаем значение F-статистики по формуле (35):

F=69,52.

a) находим с помощью стандартной статистической функции FРАСПОБР(α; р; n-p-1) значение F_кр:

F_кр=F_кр(α; k₁=p, k₂=n-p-1)=3,89.

Вывод: уравнение регрессии значимо, т.к. F> F_кр..

Вычисляя величину P-значения с помощью стандартной статистической функции FРАСП(F;p;n-p-1)(P=2,51·10^-10< α), убеждаемся в значимости уравнения регрессии.

b) для получения доверительного интервала для отдельных значений зависимой переменной у_i находим несмещенную оценку дисперсии 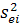регрессивного прогноза по формуле (43), проводя расчеты скалярных величин 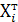( 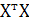)^-1х_i с помощью комбинации стандартных функцийМУМНОЖ (МУМНОЖ ( 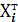; (Х^ТХ)^-1);х_i ). При этом в качестве вектора-строки 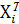берем i-ю строку матрицы Х, а в качестве вектора х_i – i-ый столбец матрицы Х^Т. Полученные значения помещаем в 9, 10 столбцы таблицы 11.

Нижние у_{i min} и верхние у_{i max} границы доверительного интервала для каждого у_i определяемпо формуле (44) и вносим их значения в столбцы 11, 12 таблицы 11.

Таблица 11

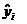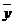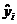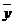i	yi	Xi1	Xi2		(yi - )2	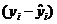( - )2	2	sei2	sei	yi min	yi max
				17,8	102,7	234,7	26,9	17,4	4,2	8,7	26,9
				21,5	229,0	135,8	12,1	16,9	4,1	12,5	30,4
				23,7	37,6	88,8	10,8	20,9	4,6	13,7	33,7
				31,9	17,1	1,6	8,3	15,5	3,9	23,3	40,5
				44,8	97,4	136,5	3,3	16,4	4,0	36,0	53,6
				29,4	102,7	14,2	40,5	16,5	4,1	20,5	38,2
				52,3	478,2	366,4	7,4	18,2	4,3	43,0	61,6
				42,5	192,3	88,3	20,0	16,5	4,1	33,7	51,4
				30,6	3,5	6,6	19,7	16,3	4,0	21,8	39,3
				40,5	23,7	54,1	6,2	16,2	4,0	31,7	49,2

Продолжение табл. 11

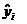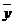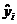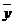i	yi	Xi1	Xi2		(yi - )2	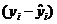( - )2	2	sei2	sei	yi min	yi max
				14,3	366,1	356,1	0,1	20,5	4,5	4,4	24,1
				50,1	319,2	286,2	0,9	18,8	4,3	40,6	59,5
					172,5	171, 5	0,0	16,7	4,1	11,1	28,9
				38,6	34,4	30,1	0,1	17,4	4,2	29,5	47,7
				39,1	3,5	35,6	16,8	15,7	4,0	30,5	47,7
S					2179,7	2006,6	173,2
ср.	33,1
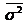					155,7	1003,3	14,4
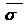					12,5	31,7	3,8

Задания для модели множественной регрессии

Задача № 1

Торговое предприятие имеет несколько филиалов. Руководство предприятия решает вопрос об открытии еще одного филиала. Для принятия обоснованного решения необходимо знать, как годовой товарооборот отдельного филиала зависит от размера торговой площади и среднедневной интенсивности потока покупателей. В таблице приведены числовые значения этих переменных для двенадцати филиалов.

Номер филиала	Товарооборот (yi)	Торговая площадь (xi2)	Интенсивность потока покупателей (xi3)
	2,93	0,31	10,24
	5,27	0,98	7,51
	6,85	1,21	10,81
	7,01	1,29	9,89
	7,02	1,12	13,72
	8,35	1,49	13,92
	4,33	0,78	8,54
	5,77	0,94	12,36
	7,68	1,29	12,27
	3,16	0,48	11,01
	1,52	0,24	8,25
	3,15	0,55	9,31

Необходимо построить две частные модели парной регрессии.

Требуется:

1. Построить диаграммы рассеяния для каждого из факторов, включенных в модель.

2. Построить модель парной регрессии.

3. Вычислить коэффициент детерминации и скорректированный коэффициент детерминации для полученной модели, используя различные формы представления коэффициента.

4. Построить доверительные интервалы для модели при уровне значимости g = 0,05 и g = 0,01.

5. Построить интервальные прогнозы среднего и индивидуального значений зависимой переменной в модели.

6. Проверить значимость коэффициента детерминации на основании
F-теста.

Задача № 2

Изменение спроса на некоторое благо (у) у домашних хозяйств определенной структуры можно объяснить с помощью цены этого блага (х₁) и дохода домохозяйства (х₂). Соответствующая информация представлена в таблице.

yt	31,4	30,4	32,1	31,0	30,5	29,8	31,1	31,7	30,7	29,7
х1t	4,1	4,2	4,0	4,6	4,0	5,0	3,9	4,4	4,5	4,8
х2t

Требуется:

1. Оценить с помощью МНК параметры линейного двухфакторного уравнения y_t = a₀ + a₁ х_1t +a₂ х₂+ e_t и интерпретировать оценки.

2. Оценить дисперсию ошибки s_e².

3. Рассчитать оценку математического ожидания 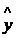при х₁=5,5 и х₂=980.

Задача № 3

На основании данных из задачи № 2 построено двухфакторное уравнение регрессии. Установлено, что ошибки e_t этого уравнения имеют нормальное распределение.

Требуется:

1. Определить одномерные 95%-е доверительные интервалы для параметров регрессии a₀, a₁ и a₂.

2. Определить 95%-й доверительный интервал дисперсии ошибки s_h².

Задача № 4

На основании данных из задачи № 2 построено двухфакторное уравнение регрессии.

Установлено, что ошибки e_t этого уравнения имеют нормальное рас­пределение.

Требуется:

1. Для уровня значимости a=0,01 проверить гипотезы H₀₀:a₀=a₀₀=12,0; H₁₀: a₁=a₁₀= –1,5; H₂₀: a₂=a₂₀=0,01.

2. Для уровня значимости a=0,01 проверить гипотезу H₀:s_e²=s₀²=0,01.

Задача № 5

В таблице представлена информация о Т=10 значениях двух объясняющих переменных x₁, x₂ и целевой функции y.

x1t	10,3	18,5	16,3	22,5	10,5	16,8	14,0	19,1	13,0	18,0
x2t	2,5	8,6	3,7	6,5	7,8	9,1	1,9	2,7	3,0	5,2
Y	24,8	48,3	37,0	51,8	29,1	43,0	30,1	41,0	29,1	40,1

Tребуется:

1. Оценить с помощью МНК параметры линейного двухфакторного уравнения регрессии y_t = a₀ + a₁ х_1t +a₂ х₂+ e_t.

2. Рассчитать значение коэффициента детерминации D и интерпретировать его.

3. Определить корреляционный вектор r и корреляционную матрицу Q.

4. Проверить для этого примера равенство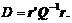

5. Определить скорректированный коэффициент детерминации 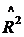и сравнить его со значением обычного коэффициента детерминации D.

Варианты для множественной регрессионной модели

Вариант № 1

	48,72	53,01	51,39	73,71	67,16	69,27	42,09

Вариант № 2

	46,22	51,11	49,09	71,51	64,46	66,67	39,99

Вариант № 3

	47,22	50,41	49,39	70,61	65,16	67,07	40,59

Вариант № 4

	45,92	48,81	47,59	67,91	62,56	64,47	39,69

Вариант № 5

	47,62	49,41	48,79	68,01	63,76	65,47	41,39

Вариант № 6

	36,52	36,61	36,19	52,51	49,56	51,07	31,09

Вариант № 7

	35,42	33,71	34,09	48,31	47,06	48,27	30,19

Вариант № 8

	35,42	34,61	35,59	52,51	50,96	52,17	28,99

Вариант № 9

	40,32	41,91	42,49	63,31	59,86	61,37	32,89

Вариант № 10

	49,52	52,21	52,19	74,11	69,56	71,27	42,09

Вариант № 11

	36,22	38,01	37,79	56,61	52,36	54,07	29,99

Вариант № 12

	52,12	51,91	51,29	79,51	66,26	67,97	43,89

Вариант № 13

	37,52	35,91	35,69	49,11	47,46	48,77	32,89

Вариант № 14

	49,92	51,81	50,59	69,01	64,36	66,17	44,29

Вариант № 15

	49,92	50,91	51,09	70,11	66,86	68,37	43,29

Вариант № 16

	40,72	40,81	40,39	56,71	53,76	55,27	35,29

Вариант № 17

	42,92	46,51	45,09	66,41	60,46	62,47	36,49

Вариант № 18

	58,02	62,61	61,19	84,41	77,76	79,87	50,99

Вариант № 19

	44,72	46,61	45,39	63,81	59,16	60,97	39,09

Вариант № 20

	37,92	39,21	39,59	59,51	56,16	57,67	30,89

Вариант № 21

	42,82	43,81	43,99	63,01	59,76	61,27	36,19

Вариант № 22

	47,12	49,21	48,79	68,91	64,56	66,27	40,49

Вариант № 23

	51,12	50,71	51,29	68,31	66,26	67,57	44,89

Вариант № 24

	53,12	57,01	55,79	78,01	71,96	73,97	46,29

Вариант № 25

	43,12	45,71	44,29	63,71	58,46	60,37	37,29

Вариант № 26

	53,12	56,61	55,79	77,91	72,36	74,27	46,09

Вариант № 27

	49,52	51,21	51,19	71,21	67,36	68,97	42,69

Вариант № 28

	43,72	48,01	46,39	68,71	62,16	64,27	37,09

Вариант № 29

	47,22	5,51	48,89	69,31	63,46	65,47	41,19

Вариант № 30