Формулы алгебры высказываний

Высказыванием называется повествовательное предложение, о котором в данной ситуации можно сказать, что оно истинно или ложно, но не то и другое одновременно.

В качестве примеров высказываний приведем предложения "Владивосток — крупнейший город Приморья" и "Снег зеленый". Первое высказывание является истинным, а второе — ложным.

Поставим в соответствие высказыванию Р логическую переменную х, которая принимает значение 1, если Р истинно, и 0, если Р ложно.

Если имеется несколько высказываний, то из них можно об­разовать различные новые высказывания. При этом исходные высказывания называются простыми, а вновь образованные — сложными. Соответственно из логических переменных можно составлять различные конструкции, которые образуют формулы алгебры высказываний.

Итак, пусть {х_i│i 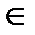I}— некоторое множество логических переменных. Определим по индукции понятие формулы алгебры высказываний (АВ):

1) любая логическая переменная является формулой АВ
(называемой атомарной);

2) если φ и ψ— формулы АВ, то выражения φ, (φ∧ψ),
(φ∨ψ), (φ→ψ) являются формулами АВ;

3) никаких других формул АВ, кроме построенных по пп. 1 и 2, нет.

Если формула φ АВ построена из логических переменных, принадлежащих множеству{х₁,х₂,…,x_n}, то будем писать φ(x₁,…x_n).

Символы , ∧, ∨ →, использованные в определении, называются логическими операциями или связками и читаются соответственно: отрицание, конъюнкция, дизъюнкция и импликация.

Введенные в п. 2 формулы следующим образом интерпретируются в русском языке: φ — "не φ", (φ∧ψ) —φ и ψ, (φ 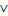ψ) — φили ψ, ( φ → ψ) —если φ,то ψ.

Вместо φчасто пишут 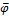,вместо ( φ∧ψ) — (φ&ψ), (φ • ψ) или (φψ).

Действия логических операций задаются таблицами истинности, каждой строке которых взаимно однозначно сопоставляется набор значений переменных, входящих в формулу, и соответствующее этому набору значение полученной формулы:

φ	φ

φ	ψ	(φ∧ψ)	(φ∨ψ)	(φ → ψ)

Пример 1. Построить таблицу истинности для формулы φ 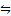((x→y)∧((y→z)→x)).

Решение.Будем строить таблицу истинности последовательно в соответствии с шагами построения формулы φ:

x	y	z	(x→y)	(y→z)	((y→z)→x)	φ

Легко заметить, что таблица истинности для φсовпадает с таб­лицей истинности для x. В дальнейшем выяснится причина этого совпадения.

Как видно из примера 1, даже при составлении несложных формул возникает обилие скобок. Чтобы избежать этого, в алгебре высказываний так же, как и в арифметике, приняты некоторые соглашения относительно расстановки скобок. Перечислим эти соглашения.

1. Внешние скобки не пишутся. Например, вместо высказывания ((x∨y)→z)пишется (x∨y)→z.

2. На множестве {, ∧, ∨, →} вводится транзитивное отношение "быть более сильным" следующим образом: наиболее сильная связка – , далее идут ∧ и∨, самая слабая связка – →.

Согласно этим отношениям недостающие скобки в формуле расставляются последовательно, начиная с наиболее сильных связок и кончая наиболее слабыми, а для связок одинаковой "силы" расстановка скобок выполняется слева направо.

Пример 2. В формуле ((x∨y)→z)→u))все скобки можно опустить:х∨y→z→u.

Эквивалентность формул АВ

Как показано в примере 1, различные формулы могут иметь одинаковые таблицы истинности. Так возникает понятие экви­валентности формул.

Формулы φ(x₁,…,x_n) и ψ(x₁,…,x_n) называются эквивалентными (φ ≡ ψ), если совпадают их таблицы истинности, т. е. ψ(е₁,…,e_n) = φ(e₁,…,e_n) для любых e₁,…,e_n 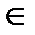{0,1}

Пример 3. Построив таблицы истинности формул x→y и y→x, убеждаемся, что (х→y) ≡ (y→x).

Легко видеть, что отношение ≡ является отношением эк­вивалентности, т. е. оно рефлексивно (φ≡φ), симметрично (еслиφ≡ψ, тоψ≡φ),транзитивно (если φ≡ψиψ≡χ, тоφ≡χ).

Отметим основные эквивалентности между формулами АВ:

1) φ∧φ≡φ, φ∨φ≡φ (законы идемпотентности);

2) φ∧ψ≡ψ∧φ, φ∨ψ≡ψ∨φ (законы коммутативности);

3) (φ∧ψ)∧χ≡φ∧(ψ∧χ), (φ∨ψ)∨χ≡φ∨(ψ∨χ) (законы ассоциативности);

4) φ∧(ψ∨χ)≡(φ∧ψ)∨(φ∧χ), φ∨(ψ∧χ)≡(φ∨ψ)∧(φ∨χ) (законы дистрибутивности)

5) (φ∧ψ)≡φ∨ψ, (φ∨ψ)≡φ∧ψ (законы де Моргана);

6) φ≡φ (закон двойного отрицания);

7) φ→ψ≡φ∨ψ;

8) φ∧(φ∨ψ)≡φ, φ∨(φ∧ψ)≡φ (законы поглощения);

9) φ∨(φ∧ψ)≡φ∨ψ, φ∨(φ∧ψ)≡φ∨ψ;

10) φ∧(φ∨ψ)≡φ∧ψ, φ∧(φ∨ψ)≡φ∧ψ.

Формула φ(x₁,x₂,…,x_n) называется выполнимой (опровержимой), если существует такой набор значений переменных, на котором формула принимает значение 1 (соответственно 0) .

Пример 4. Формула х∧у является одновременно выполнимой и опровержимой, поскольку 0∧0=0, а 1∧1=1.

Формула φ(x₁,…,x_n)называется тождественно истинной, общезначимой или тавтологией (тождественно ложной или противоречием), если эта формула принимает значение 1 (соответственно 0) на всех наборах значений переменных.

Пример 5. Формула x∨x является тождественно истинной, а формула x∧x — тождественно ложной:

x	x∨x	x∧x

Утверждение 1. Если формула φ₁тождественно истинна, φ₀ — тождественно ложна, то для любых формул φи ψсправедливы следующие эквивалентности:

1) φ∧ φ₁≡φ; φ∨φ₀≡φ;

2) φ∨φ₁≡φ₁; φ∧φ₀≡φ₀;

3) (φ∧ψ→φ)≡φ₁; (φ→φ∨ψ)≡φ₁.