Лекция 1. Введение. Структура механизмов.
Примеры.
Класс кинематической паре присваивается по числу связей U.
Степень свободы механизма
Различают механизмы плоские и пространственные.
Степень свободы пространственных механизмов считают по формуле Сомова-Малышева:
W=6n-5p5-4p4-3p3-2p2-p1,
где n- число подвижных звеньев;
p5,p4,p3,p2,p1- число кинематических пар пятого, четвертого, третьего, второго и первого классов соответственно.
Степень свободы плоских механизмов считают по формуле Чебышева:
W=3n-2p5-p4
Степень свободы плоского механизма должна быть равна числу ведущих звеньев, то есть W=1.
Избыточные связи- это такие связи, которые повторяют (дублируют) связи, уже имеющиеся по данной координате, и поэтому не изменяющие реальной подвижности механизма.
Примеры.
Классификация плоских механизмов по системе Л.В.Ассура.(Принцип образования плоских механизмов). Согласно идее Л.В.Ассура, механизмы состоят из отдельных кинематических цепей- структурных групп (групп Ассура), степень свободы которых равна нулю (W=0).
Кроме того, механизм должен содержать только кинематические пары 5 класса (р5), если же есть пары 4 класса (р4), то одну пару р4 заменяют на звено и две пары р5 . Полученный после такой замены механизм называют заменяющим.
Так как W=0, р4=0, то из формулы Чебышева следует:
3n-2p5=0
p5=3n/2
| n | ||||
| p5 |
Структурная группа- это кинематическая цепь, степень свободы которой равна нулю и она не должна распадаться на более простые кинематические цепи, удовлетворяющие этому условию. Число звеньев в структурной группе должно быть четным, а число пар пятого класса кратно трем.
Примеры.
Структурная группа I класса- это ведущее звено со стойкой, соединенные парой пятого класса (W=1) (рис.1).
Структурная группа II класса состоит из двух звеньев и трех кинематических пятого класса ( вращательные или поступательные).
Начиная с III класса, номер группе присваивается в зависимости от числа внутренних кинематических пар (внешние кинематические пары служат для соединения с другими группами).

Рис.1
Лекция 2. Кинематический анализ механизмов
Вопросы, рассматриваемые на лекции. План положения механизма. Теорема Грасгофа (условие существования кривошипа). Масштабные коэффициенты. Определение скорости и ускорения методом планов.
Некоторые основные понятия.
Теорема Грасгофа: наименьшее звено является кривошипом, если сумма длин его и любого другого звена меньше суммы длин остальных звеньев.
Кинематический анализ- изучение движения звеньев механизма вне зависимости от сил, действующих на эти звенья.
План положений механизма- графическое изображение взаимного расположения звеньев механизма в определенный момент времени.
Планами скоростей и ускорений называют векторные изображения этих параметров в заданном положении механизма.
Масштабный коэффициент физической величины- отношение численного значения физической величины в свойственных ей единицах к длине отрезка в миллиметрах, изображающего эту величину.
Примеры.
Лекция 3. Построение кинематических диаграмм.
Вопросы, рассматриваемые на лекции.
Кинематическое исследование механизмов аналитическими методами. Кинематический анализ шарнирного четырехзвенника. Кинематический анализ кривошипно-ползунного механизма. Кинематический анализ кривошипно-кулисного механизма.
Некоторые основные понятия.
Лекция 17. Основные понятия теории машин-автоматов.
Вопросы, рассматриваемые на лекции. Основы теории роботов-манипуляторов. Структура кинематических цепей роботов-манипуляторов. Циклограммы и тактограммы технологических машин.
Некоторые основные понятия.
Машина-автомат- машина, в которой преобразования энергии, материалов и информации выполняются без участия человека.
Автоматическая линия- совокупность машин-автоматов, соединенный между собой транспортными устройствами и предназначенных для выполнения определенного технологического процесса.
Исполнительное звено- каждое твердое тело машины-автомата, выполняющее заданные перемещения с целью обеспечения технологического процесса.
Числовое программное обеспечение. Самонастраивающаяся система управления.
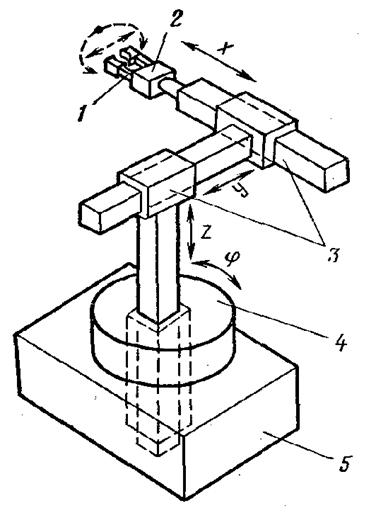
Рис.47
Манипулятор- это техническое устройство, автоматически воспроизводящее функции руки человека при выполнении вспомогательных и транспортных производственных операций посредством перемещения объекта в пространстве.
Автооператор- манипулятор, работающий по жесткой программе и оперирующий штучными объектами по общему циклу машины.
Промышленный робот- манипулятор с изменяемой программой, представляющий собой автономно функционирующую машину-автомат, предназначенную для воспроизведения некоторых двигательных и умственных функций человека при выполнении вспомогательных и основных производственных операций.
Оглавление
Лекция 1. Введение. Структура механизмов. 1
Лекция 2. Кинематический анализ механизмов. 6
Лекция 3. Построение кинематических диаграмм. 9
Лекция 4. Кинематический анализ и синтез кулачковых механизмов. 11
Лекция 6. Синтез эвольвентного зубчатого зацепления. 16
Лекция 7. Синтез многозвенных зубчатых механизмов. 20
Лекция 8. Механизмы передач с гибкими звеньями. Винтовые механизмы. 23
Лекция 9. Механизм универсального шарнира. Механизм двойного универсального шарнира. 24
Лекция 10. Механизмы фрикционных передач. Мальтийский механизм. Гидравлические пневматические механизмы. 26
Лекция 11. Динамический анализ механизмов. 28
Лекция 12. Механическая характеристика машины. 29
Лекция 13. Движение механизмов машины под действием приложенных сил. 30
Лекция 14. Неравномерность хода машины при установившемся движении. 32
Лекция 15. Трение в кинематических парах. 37
Лекция 16. Виброзащита механизмов и машин. Уравновешивание вращающихся звеньев. 38
Лекция 17. Основные понятия теории машин-автоматов. 40
Лекция 1. Введение. Структура механизмов.
Вопросы, рассматриваемые на лекции. ТММ - научная основа новых машин и механизмов. Исторический очерк развития ТММ. Цели и задачи курса. Разделы ТММ. Основные виды звеньев. Кинематические пары. Степень подвижности механизмов. Структурная классификация механизмов. Условия существования кривошипа. Модификация механизмов при замене пар.
Некоторые основные понятия.
Теория механизмов и машин (ТММ)- наука, изучающая строение, кинематику и динамику механизмов в связи с их анализом и синтезом.
ТММ включает три основные части:
1. Структурный и кинематический анализ механизмов- изучение теории строения механизмов, исследование движения тел образующих механизм с точки зрения геометрии без учета сил, вызывающих движение этих тел.
2. Синтез механизмов- проектирование механизмов по заданным кинематическим и динамическим условиям.
3. Динамический анализ механизмов- определение сил, действующих на звенья механизма во время их движения, изучение взаимосвязи между движениями тел, их массами и силами действующими на них.
Машина- это устройство, создаваемое человеком, для облегчения физического и умственного труда, увеличения производительности путем частичной или полной замены человека.
Машина- устройство для преобразования энергии, информации или материалов.
Машины состоят из механизмов.
Механизм- система тел, предназначенная для преобразования движения одних тел (одного или нескольких) в требуемое движение других.
Например: механизм подачи заготовок, механизм сцепления, механизм торможения и т.д.
Механизмы состоят из звеньев и кинематических пар.
Звено- одно или несколько жестко соединенных твердых тел.
Кинематическая пара- соединение двух звеньев, допускающее относительное движение.
Звенья различают входные (ведущие), выходные (ведомые) и промежуточные.
Основные виды звеньев: стойка, кривошип, коромысло, ползун, кулиса, кулачок, зубчатое колесо.
Кроме перечисленных жестких звеньев, в механизмах применяют гибкие (цепи, ремни), упругие (пружины, мембраны) звенья, а также жидкие и газообразные (масло, вода, газ, воздух и т.д.).
Звенья обозначают цифрами, причем нумерация ведется от ведущего звена, а стойке присваивается «ноль».
Кинематические пары обозначают заглавными латинскими буквами (A,B,C,D и т.д.).
Основные виды кинематических пар (таблица 1)


Кинематическая схема механизма – чертеж механизма в выбранном масштабе с соблюдением условных обозначений звеньев и кинематических пар.
Различают кинематические пары высшие и низшие.
Высшая кинематическая пара – звенья соприкасаются по линии или в точке.
Низшая кинематическая пара – звенья соприкасаются по поверхностям (цилиндрический или шаровой шарниры, ползун и кулиса)
Различают кинематические пары с геометрическим и силовым замыканием
Геометрическое замыкание (характерно для низших пар) – соприкосновение элементов звеньев обеспечивается их формами (цилиндрический шарнир, шаровой шарнир, ползун и кулиса).
Силовое замыкание (характерно для высших пар) – соприкосновение обеспечивается силой веса, силой сжатия пружины и т.д.
Высшие пары изнашиваются сильнее, чет низшие, так как чем больше поверхности, тем меньше удельное давление (давление на единицу площади).
Различают пять классов кинематических пар.
Свободно движущееся в пространстве тело имеет шесть степеней свободы(W) – шесть движений (три поступательных, три вращательных).

Основные типы звеньев механизмов (таблица 2)
 |
Если же тело связано с другими телами, то на его движения накладываются ограничения – условия связи (U), тогда число степеней свободы не равно шести, оно уменьшается.
W=6-U
Примеры.
Класс кинематической паре присваивается по числу связей U.
Степень свободы механизма
Различают механизмы плоские и пространственные.
Степень свободы пространственных механизмов считают по формуле Сомова-Малышева:
W=6n-5p5-4p4-3p3-2p2-p1,
где n- число подвижных звеньев;
p5,p4,p3,p2,p1- число кинематических пар пятого, четвертого, третьего, второго и первого классов соответственно.
Степень свободы плоских механизмов считают по формуле Чебышева:
W=3n-2p5-p4
Степень свободы плоского механизма должна быть равна числу ведущих звеньев, то есть W=1.
Избыточные связи- это такие связи, которые повторяют (дублируют) связи, уже имеющиеся по данной координате, и поэтому не изменяющие реальной подвижности механизма.
Примеры.
Классификация плоских механизмов по системе Л.В.Ассура.(Принцип образования плоских механизмов). Согласно идее Л.В.Ассура, механизмы состоят из отдельных кинематических цепей- структурных групп (групп Ассура), степень свободы которых равна нулю (W=0).
Кроме того, механизм должен содержать только кинематические пары 5 класса (р5), если же есть пары 4 класса (р4), то одну пару р4 заменяют на звено и две пары р5 . Полученный после такой замены механизм называют заменяющим.
Так как W=0, р4=0, то из формулы Чебышева следует:
3n-2p5=0
p5=3n/2
| n | ||||
| p5 |
Структурная группа- это кинематическая цепь, степень свободы которой равна нулю и она не должна распадаться на более простые кинематические цепи, удовлетворяющие этому условию. Число звеньев в структурной группе должно быть четным, а число пар пятого класса кратно трем.
Примеры.
Структурная группа I класса- это ведущее звено со стойкой, соединенные парой пятого класса (W=1) (рис.1).
Структурная группа II класса состоит из двух звеньев и трех кинематических пятого класса ( вращательные или поступательные).
Начиная с III класса, номер группе присваивается в зависимости от числа внутренних кинематических пар (внешние кинематические пары служат для соединения с другими группами).

Рис.1
