Основные законы и уравнения цепей с сосредоточенными параметрами.

Цепи, содержащие источники энергии, резисторы, индуктивные катушки и конденсаторы, могут быть представлены схемами замещения, состоящими из источников э.д.с., тока и элементов r, L, С. В схеме с сосредоточенными параметрами необратимые потери энергии происходят только в сопротивлениях, магнитное поле связано только с индуктивностями, ток смещения, обусловленный изменяющимся электрическим полем, имеет место только в емкостях.

Основные уравнения для цепей с сосредоточенными параметрами вытекают из известных физических законов — принципа непрерывности полного тока и закона электромагнитной индукции.

Из принципа непрерывности полного тока следует:

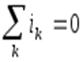(1.12)

где i_k — ток k-го проводника, присоединенного к рассматриваемому узлу.

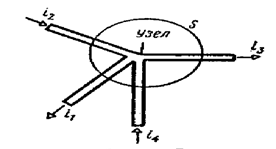
Уравнение (1.12) называют первым законом Кирхгофа, который формулируется следующим образом: алгебраическая сумма токов ветвей, соединенных в узле, равна нулю в любой момент времени. При этом с положительным (отрицательным) знаком учитывают токи, направленные от узла (к узлу).

Для узла на рис. 1.17 уравнение по первому закону Кирхгофа записывается следующим образом:

i₁-i₂+i₃-i₄=0.

Если в уравнении (1.12) токи источников тока перенести в правую часть, то получается

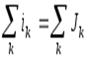, (1.13)

где 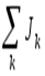— алгебраическая сумма токов источников тока; 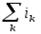— алгебраическая сумма токов других ветвей (элементов). В уравнении (1.13) с положительным (отрицательным) знаком записывают ток источника J_k, направленный к узлу (от узла), и ток i_k, направленный от узла (к узлу).

Например, если ток i₄ представляет собой ток источника тока, т. е. i₄=J₄ (рис. 1.17), то в соответствии с равенством (1.13)

i₁-i₂+i₃=J₄.

Из закона электромагнитной индукции следует:

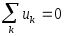(1.16)

Уравнение (1.16) называют вторым законом Кирхгофа, который формулируется следующим образом: алгебраическая сумма напряжений на зажимах ветвей (элементов) контура равна нулю в любой момент времени. При этом с положительным (отрицательным) знаком учитывают напряжения, положительные направления которых совпадают (противоположны) направлению обхода контура.

На рис. 1.18 показан пример контура цепи; путь интегрирования 1-а-2-3-б-4-1 содержит зажимы элементов. Для выбранного пути интеграл в равенстве (1.15) разбивается на четыре слагаемых:

-u₁+u₂-u₃+u₄=0,

где

u₁=j₂-j₁; u₂=j₂-j₃; u₃=j₄-j₃; u₄=j₄-j₁.

Если напряжения источников перенести в правую часть равенства (1.16) и заменить на э. д. с., то второму закону Кирхгофа соответствует уравнение

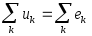, (1.17)

которое выражает равенство алгебраических сумм напряжений на пассивных элементах и э. д. с. контура. В уравнении (1.17) с положительным (отрицательным) знаком записывают напряжения и э. д. с., направление которых совпадает (противоположно) с направлением обхода контура.

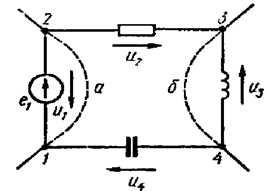
Например, для контура на рис. 1.18 по второму закону Кирхгофа записывают (выбирая направление обхода по часовой стрелке совпадающим с направлением э. д. с. e₁)

u₂-u₃+u₄=e₁

Уравнения (1.12), (1.16) или (1.13) и (1.17) совместно с соотношениями (1.3), (1.4), (1.6), (1.7), (1.9), (1.10), связывающими напряжения и токи каждого элемента, дают полное математическое описание цепи.

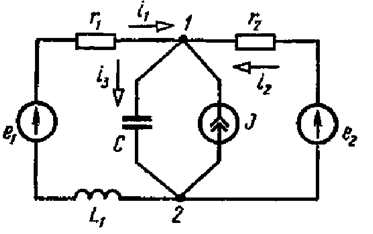
Пример 1.1.Составить уравнения Кирхгофа для схемы на рис. 1.19.

Решение. Для узлов 1 и 2, по первому закону Кирхгофа,

-i₁-i₂+i₃=J;

i₁+i₂-i₃=-J.

Одно из записанных уравнений является зависимым.

Для контура е₁ — r₁ — С — L₁(при направлении обхода контура по часовой стрелке), по второму закону Кирхгофа,

.

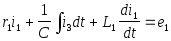Положительные направления напряжений на зажимах пассивных элементов приняты совпадающими с положительными направлениями токов и учтены выражения (1.3), (1.10), (1.6). Для контура С — r₂ —е₂ (направление обхода по часовой стрелке)

.

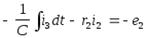Для контура е₁ — r₁ — r₂ — е₂ — L₁(направление обхода по часовой стрелке)

.

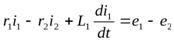Последнее уравнение, записанное по второму закону Кирхгофа, равно сумме двух предыдущих уравнений.

Таким образом, из пяти уравнений Кирхгофа для схемы на рис. 1.19 независимыми являются три уравнения (одно для какого-либо узла и два других для любых двух контуров схемы).