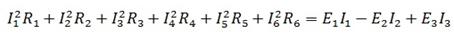Источники и потребители энергии в цепи (активные и пассивные двухполюсники). Баланс мощности.
Основная задача электротехники. Основные понятия (эл. цепь, схема цепи, элементы цепи, ветви, узлы, контуры). Процессы, происходящие в цепях. Принципы наложения и взаимности. Их описание с помощью уравнений.
Основные задачи в области электротехники:
1. Расчеты и анализы цепей, т.е. определение связи между токами, напряжениями, параметрами заданной цепи и теми величинами, которые определяют работу рассматриваемой установки (например: к.п.д., падение напряжения, величина тока к.з. и т.д.). Также сюда входят и задачи математического описания цепей (геометрия и топология цепей, их матрицы); методы решения и анализа систем уравнений электрических цепей.
2. Принцип работы и общие свойства важнейших электротехнических устройств и элементов электрической цепи. Например, вопрос о согласовании приемника к источникам питания для получения максимальной мощности; теория резонанса.
3. Синтез электрических цепей.
Задачи синтеза заключаются в разработке методов такого выбора схемы соединения элементов цепи и такого подбора параметров этих элементов, чтобы полученная цепь обладала заданными характеристиками. Например, такой простой вопрос, как выбор параметров треугольника, эквивалентного заданной звезде, по существу относится к задаче синтеза.
4. Оптимизация электрических цепей. В том числе параметрическая оптимизация, т.е. выбор таких параметров цепи, которые соответствуют достижению целевой функции.
Электрическая цепь – совокупность устройств, предназначенных для прохождения в них электрического тока, электромагнитные процессы в которой могут быть описаны с помощью понятий: ток, напряжение (разность потенциалов), электродвижущая сила, заряд, магнитный поток, сопротивление, индуктивность, взаимная индуктивность и емкость.
Чтобы задать эл. цепь, нужно знать
1) из каких элементов (устройств) она состоит;
2) и как эти элементы друг с другом соединяются (топологию цепи).
Для линейных электрических цепей справедлив принцип наложения, согласно которому ток (напряжение) любой ветви равен сумме частичных токов (напряжений), создаваемых в этой ветви каждым из источников в отдельности. Этот принцип лежит в основе метода наложения. Метод наложения применим только для расчета линейных цепей.
Частичный ток – ток в ветви от действия только одного источника энергии, когда все остальные источники приняты нулевыми. Пусть в цепи действуют nидеальных источников ЭДС и m идеальных источников тока. Тогда ток в i-ой ветви может быть определен как
Расчёт цепей постоянного тока (последовательное, параллельное, смешанное соединение, соединение «звезда» и «треугольник»)
Метод сворачивания
Этот метод применяется только для электрических цепей содержащих один источник питания. Для расчета, отдельные участки схемы, содержащие последовательные или параллельные ветви, упрощают, заменяя их эквивалентными сопротивлениями. Таким образом, цепь свертывается до одного эквивалентного сопротивления цепи подключенного к источнику питания.
Затем определяется ток ветви, содержащий ЭДС, и схема разворачивается в обратном порядке. При этом вычисляются падения напряжений участков и токи ветвей. Так, например, на схеме 2.1 А Сопротивления R3 и R4 включены последовательно. Эти два сопротивления можно заменить одним, эквивалентным
R3,4=R3+R4
После такой замены получается более простая схема(Рис.2.1Б).
Здесь следует обратить внимание на возможные ошибки в определении способа соединений сопротивлений. Например сопротивления R1 и R3 нельзя считать соединенными последовательно, также как сопротивления R2 и R4 нельзя считать соединенными параллельно, т. к. это не соответствует основным признакам последовательного и параллельного соединения.
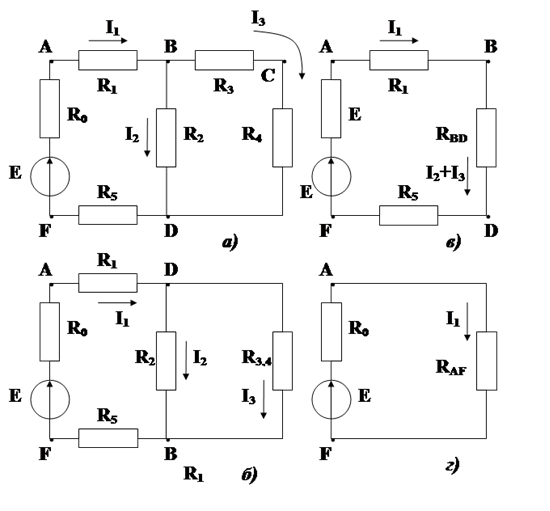
Метод уравнений Кирхгофа.
Пусть требуется рассчитать цепь, показанную на рис. 2.
Задаемся положительным направлением токов и напряжений (произвольно).
Составляем уравнения по законам Кирхгофа.
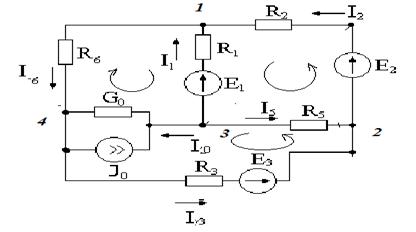
В цепи 4 узла значит по I з. Кирхгофа можно составить 3 уравнения.
Пронумеруем узлы.
Для узла № 1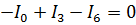 
,
Для узла № 2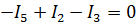 
,
Для узла № 3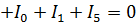 
.
В цепи три независимых контура значит по II з.К. можно составить 3 уравнения. Зададимся направлением обхода контуров (произвольно) и покажем стрелкой
Для контура R1- E1-E0-R0-R6: -R6I6- R1I1+ R0I0=- E1- E0 ,
Дляконтура R1- E1-E2-R2-R5: -R1 I1+ R5 I5+ R2 I2=+ E2- E1 ,
Дляконтура R3- E3-E0-R0-R5: R0I0+ R3 I3-R5 I5=+ E3- E0.
Получили систему из шести уравнений для шести неизвестных – токов в ветвях.
Можно заметить, что чем больше ветвей, а значит больше токов, сложность решения возрастает. Нужно использовать пакеты стандартных программ и решать с помощью компьютера или искать другие методы решения.
МЕТОД УЗЛОВЫХ ПОТЕНЦИАЛОВ
В методе уравнений Кирхгофа искомыми являются токи в ветвях и соответственно с этим число подлежащих решению уравнений равно числу ветвей, т.е.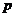 
.
Число решаемых (совместно) уравнений можно уменьшить, если в качестве искомых величин принять потенциалы узлов. Знание этих потенциалов позволяет найти все токи в схеме. Уравнения с узловыми потенциалами (узловые уравнения) вытекают из первого закона Кирхгофа; число этих уравнений равно числу независимых узлов,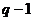 
.
Порядок решения.
1. Нумеруются все узлы.
2. Произвольно задают положительные направления токов в ветвях.
3. Потенциал одного узла принимается равным нулю, а этот узел называется базисным. NB: Если какая-нибудь ветвь содержит один идеальный источник ЭДС, за базисный узел принимается один из ее узлов, тогда потенциал другого будет равен ±Е.
4. Составляются узловые уравнения относительно оставшихся узлов, в результате решения которых находят их потенциалы.
5. Зная потенциалы узлов, т.е. напряжения на ветвях, по II закону находят токи во всех ветвях. NB: Если ток получился отрицательным, необходимо изменить ранее выбранное направление на противоположное.
6. Проверку осуществляют по I закону Кирхгофа.
Пример.
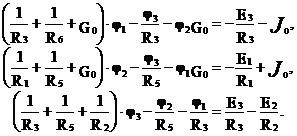
Правило знаков правой части: если источник направлен от узла, он записывается со знаком «-».
В скобках – собственное проводимость узла; остальные проводимость связи между парой узлов.
Потенциалы в отличие от токов могут принимать отрицательное значение.
По II закону Кирхгофа, составим уравнения для нахождения токов во всех ветвях цепи
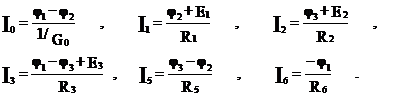
NB: метод узловых потенциалов целесообразно применять, когда количество узлов, уменьшенное на 1, меньше количества независимых контуров.
При большом количестве узлов узловые уравнения записываются в матричной форме и решаются с помощью компьютера.
9. 
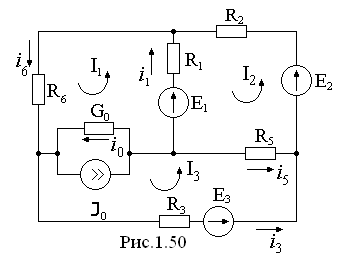МЕТОД КОНТУРНЫХ ТОКОВ.
В качестве искомых величин можно принять токи ветвей связи, или так называемые контурные токи. Знание контурных токов позволяет найти все реальные токи в схеме.
Уравнения с контурными токами (контурные уравнения) получают на основе второго закона Кирхгофа; их число равно числу независимых уравнений, составленных для контуров, т.е.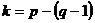 
.
Порядок решения.
7. Источники тока заменяются на эквивалентные источники ЭДС.
8. Произвольно задают положительные направления токов в ветвях.
9. Определяются независимые контура, в которые запускаются контурные токи, направление их выбирается произвольно.
10. Составляются контурные уравнения для независимых контуров и решая их находят контурные токи. NB: контурные токи могут получиться отрицательными.
11. Зная контурные токи, используя принцип наложения, находят токи во всех ветвях (с учетом знаков и направлений контурных токов). NB: Если ток получился отрицательным, необходимо изменить ранее выбранное направление на противоположное.
12. Проверку осуществляют по I закону Кирхгофа.
Пример.
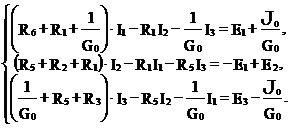
В скобках – собственное сопротивление контура; остальные – общие сопротивления.
Правило знаков правой части: если направление контурного тока совпадает с направлением источника записывают их со знаком «+», в противном случае – со знаком «-».
Основная задача электротехники. Основные понятия (эл. цепь, схема цепи, элементы цепи, ветви, узлы, контуры). Процессы, происходящие в цепях. Принципы наложения и взаимности. Их описание с помощью уравнений.
Основные задачи в области электротехники:
1. Расчеты и анализы цепей, т.е. определение связи между токами, напряжениями, параметрами заданной цепи и теми величинами, которые определяют работу рассматриваемой установки (например: к.п.д., падение напряжения, величина тока к.з. и т.д.). Также сюда входят и задачи математического описания цепей (геометрия и топология цепей, их матрицы); методы решения и анализа систем уравнений электрических цепей.
2. Принцип работы и общие свойства важнейших электротехнических устройств и элементов электрической цепи. Например, вопрос о согласовании приемника к источникам питания для получения максимальной мощности; теория резонанса.
3. Синтез электрических цепей.
Задачи синтеза заключаются в разработке методов такого выбора схемы соединения элементов цепи и такого подбора параметров этих элементов, чтобы полученная цепь обладала заданными характеристиками. Например, такой простой вопрос, как выбор параметров треугольника, эквивалентного заданной звезде, по существу относится к задаче синтеза.
4. Оптимизация электрических цепей. В том числе параметрическая оптимизация, т.е. выбор таких параметров цепи, которые соответствуют достижению целевой функции.
Электрическая цепь – совокупность устройств, предназначенных для прохождения в них электрического тока, электромагнитные процессы в которой могут быть описаны с помощью понятий: ток, напряжение (разность потенциалов), электродвижущая сила, заряд, магнитный поток, сопротивление, индуктивность, взаимная индуктивность и емкость.
Чтобы задать эл. цепь, нужно знать
1) из каких элементов (устройств) она состоит;
2) и как эти элементы друг с другом соединяются (топологию цепи).
Для линейных электрических цепей справедлив принцип наложения, согласно которому ток (напряжение) любой ветви равен сумме частичных токов (напряжений), создаваемых в этой ветви каждым из источников в отдельности. Этот принцип лежит в основе метода наложения. Метод наложения применим только для расчета линейных цепей.
Частичный ток – ток в ветви от действия только одного источника энергии, когда все остальные источники приняты нулевыми. Пусть в цепи действуют nидеальных источников ЭДС и m идеальных источников тока. Тогда ток в i-ой ветви может быть определен как
Источники и потребители энергии в цепи (активные и пассивные двухполюсники). Баланс мощности.
| Пассивные элементы (потребители энергии) | |||
| Резистор/активное сопротивление R |  |   . | |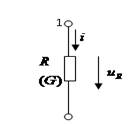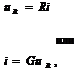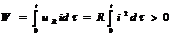
| Индуктивная катушка/индуктивность L |  |  ,   | |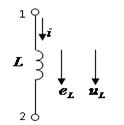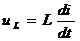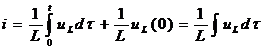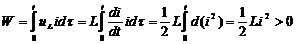
| Конденсатор/емкость C |  |  ,   | |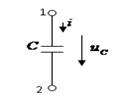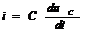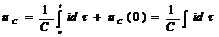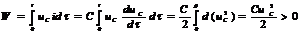
| NB В Если R, L, C – величины постоянные, то эти элементы называются линейными. Если цепь состоит из одних линейных элементов, то она считается линейной | |||
| Активные элементы (источники энергии) | |||
| Источник ЭДС (напряжения) e, E | |||
| Идеальный | 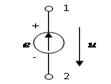 | u=  | |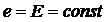
| Реальный |  |  | |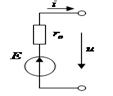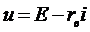
| Источник тока, J | |||
| Идеальный | 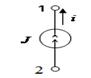 | i=J | |
| Реальный |  |  | |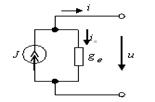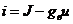
NB идеальные источники не могут быть эквивалентно преобразованы друг в друга. Используются формулы перехода:  ,  | |||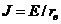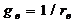
