Определение положения центра тяжести. Построение центральных осей
Определяем координаты точек С1 и С2 относительно системы z1C1y1.
Точка С1: 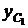 =0;
=0; 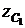 =0.
=0.
Точка С2 : 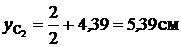 ;
; 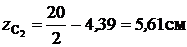 .
.
Общая площадь фигуры 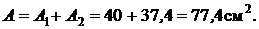
Координата центра тяжести по оси y
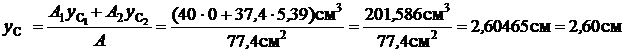 .
.
Координата центра тяжести по оси z
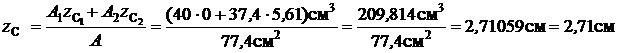 .
.
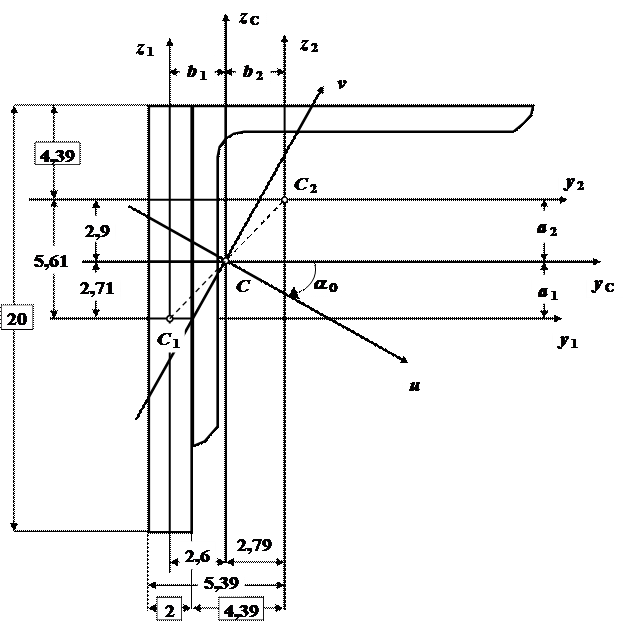 Проводим центральные оси y C , z C параллельно осям y 1 , z1 , как это показано на рис.11.
Проводим центральные оси y C , z C параллельно осям y 1 , z1 , как это показано на рис.11.
Рис.11
Замечание. Центр тяжести составной фигуры (точка С) всегда должен лежать на
прямой линии, соединяющей точка С1 и С2 (см. рис.11).
Теперь y C, z C - основная система координат.
Определение величин осевых и центробежного моментов инерции
Относительно центральных осей
Момент инерции составной фигуры относительно оси y C равен сумме моментов инерции первой и второй фигур
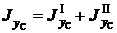 .
.
Момент инерции первой фигуры относительно оси y C равен моменту инерции относительно оси y 1 плюс площадь этой фигуры на квадрат расстояния между осями y 1 и y C (используем формулы параллельного переноса осей)
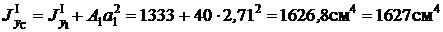 ;
;
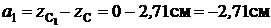 (см. рис.11).
(см. рис.11).
Момент инерции второй фигуры относительно оси y C
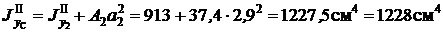 ;
;
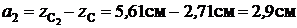 (см. рис.11).
(см. рис.11).
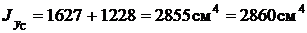 .
.
Момент инерции составной фигуры относительно оси z C равен сумме моментов инерции первой и второй фигур
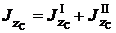 .
.
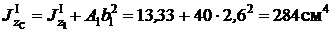 ;
;
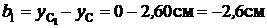 (см. рис.11).
(см. рис.11).
Момент инерции второй фигуры относительно оси y C
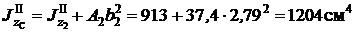 ;
;
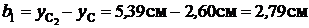 (см. рис.11).
(см. рис.11).
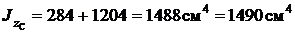 .
.
Центробежный момент инерции составной фигуры относительно осей y C, z C равен сумме центробежных моментов инерции первой и второй фигур
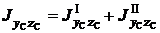 .
.
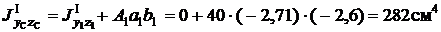 ;
;
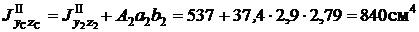 ;
;
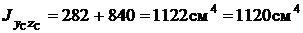 .
.
Моменты инерции относительно центральных осей найдены
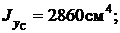
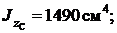
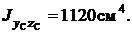
Определение направления главных центральных осей
Направление главных центральных осей определяется по формуле:
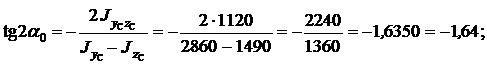
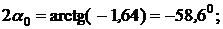
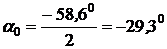 .
.
Знак “ –“ показывает, что угол 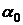 откладывается от оси y C по ходу часовой стрелки (для “ + “ – против хода часовой стрелки).
откладывается от оси y C по ходу часовой стрелки (для “ + “ – против хода часовой стрелки).
Проводим главные центральные оси u ,v , как это показано на рис.11.
Определение величин осевых моментов инерции относительно
Главных центральных осей
Моменты инерции относительно главных центральных осей вычисляются по следующим формулам:
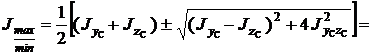
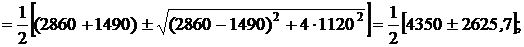
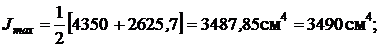
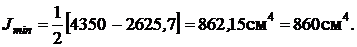
Так как 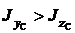 , то
, то 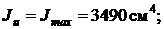
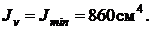
Наибольший из моментов инерции при повороте осей возрастает, достигая максимального значения, а меньший момент инерции убывает, достигая минимального значения, при этом сумма осевых моментов инерции относительно двух взаимно перпендикулярных осей остается постоянной, т.е.
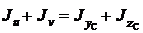 =const.
=const.
Используем последнее соотношение в качестве проверки
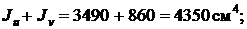
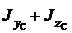 =
= 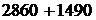 =
= 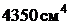 .
.
Задача 3
Для заданных двух схем балок (рис.12,15) требуется:
1.Для каждого участка балки составить выражения поперечных сил (Q) и изги-
бающих моментов(M) , используя метод сечений. Построить их эпюры.
2.Определить опасное сечение по нормальным напряжениям.
3.Из условия прочности по методу допускаемых напряжений при изгибе
подобрать:
а) для схемы (а) деревянную балку круглого поперечного сечения, приняв
допускаемое нормальное напряжение [ s ] = 10МПа;
б) для схемы (б) стальную балку двутаврового поперечного сечения, приняв
допускаемое нормальное напряжение [ s ] = 160МПа.
4. Проверить прочность балок.
Схема а)
 Исходные данные:
Исходные данные:
a=2 м; b=2 м; q=10 кН/м;
m=8 кНм; F=15 кН;
[s ] = 10МПа=10 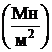 .
.
Рис.12
Решение
1.Построение эпюр поперечной силы Q и изгибающего момента M
Разбиваем расчетную схему балки на участки. Границами участка являются точки приложения сосредоточенных сил, сосредоточенных моментов, точки начала и конца распределенной нагрузки. В нашем примере балка имеет два участка, которые пронумеруем справа налево (рис. 14). Для определения внутренних усилий необходимо на каждом участке использовать метод сечений, который сводится к следующему.
1. Проводим поперечное сечение, которое разбивает балку на две части;
2. Выбираем ту часть балки, на которую действуют известные нагрузки (левую от сечения или правую);
3. Составляем выражения для поперечной силы Q и изгибающего момента M,
при этом руководствуемся определением и правилом знаков.
Определение. Поперечная сила Q – это внутренняя сила, численно равная
алгебраической сумме всех внешних сил, действующих по одну
сторону от сечения перпендикулярно оси балки.
Определение. Изгибающий момент M –это внутренний момент, численно равный
алгебраической сумме моментов всех внешних сил, действующих
по одну сторону от сечения относительно центра тяжести попереч-
ного сечения.
Правило знаков. Поперечная сила в поперечном сечении балки положительная
(Q>0), если внешние силы (Fвнеш) направлены так, как показано на рис.13.
Изгибающий момент в поперечном сечении балки положителен(M >0), если
моменты внешних сил (Mвнеш) направлены так, как показано на рис.13.
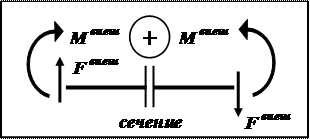 Поперечная сила и изгибающий момент отрицательны, если направления внешних сил и моментов внешних сил противоположны направлениям, указанным на рис.13.
Поперечная сила и изгибающий момент отрицательны, если направления внешних сил и моментов внешних сил противоположны направлениям, указанным на рис.13.
Рис.13
Проводим сечение на первом участке и рассматриваем правую от сечения часть балки (рис.14), т.к. слева от сечения опорные реакции неизвестны.
I участок 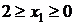 (сечение перемещается от правой до левой границы).
(сечение перемещается от правой до левой границы).
Составляем выражение для поперечной силы с учетом правила знаков справа от сечения
Q(x1)= - F + qx1= - 15 + 10x1(уравнение прямой линии).
Здесь qx1 - равнодействующая сила распределенной нагрузки q, расположенная справа от сечения посредине участка длиной x1.
Определяем значения Q на границах участка
Q(0)= - 15 + 10 · 0= - 15 кН (значение на правой границе участка);
Q(2)= -15 + 10 ·2=5 кН(значение на левой границе участка).
Поскольку поперечная сила меняет знак в пределах участка, определяем координату, при которой она обращается в нуль (в этом сечении изгибающий момент принимает экстремальное значение):
Q(x0)= - 15 + 10x0=0; x0=15/10=1,5 м.
Составляем выражение для изгибающего момента с учетом правила знаков справа от сечения
M(x1) = 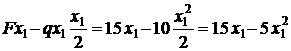 (уравнение квадратичной параболы).
(уравнение квадратичной параболы).
Определяем значения M на границах участка и в найденной точке x0
M(0)=0 (значение на правой границе участка) ;
M(1,5)= 1,5·(15 – 5·1,5)=11,25 кНм=11,3 кНм(значениев точке x0);
M(2)=2·(15 – 5·2)=10 кНм (значение на левой границе участка).
II участок 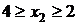 (сечение перемещается от правой до левой границы).
(сечение перемещается от правой до левой границы).
Составляем выражение для поперечной силы с учетом правила знаков справа от сечения
Q(x2)= - F + q·2= - 15 + 10·2= 5 кН (прямая линия параллельная оси x).
Составляем выражение для изгибающего момента с учетом правила знаков справа от сечения
M(x2) = 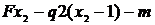 = 15x2 - 20 (x2-1) – 8 = - 5x2 + 12 (уравнение прямой).
= 15x2 - 20 (x2-1) – 8 = - 5x2 + 12 (уравнение прямой).
M(2)= - 5 ·2 + 12= 2 кНм (значение на правой границе);
M(4)= - 5 ·4 + 12= - 8 кНм (значение на левой границе).
