Указания о порядке выполнения контрольной работы

Утверждено на заседании

кафедры сопротивления

материалов 21ноября 2006 г.

Методические указания и контрольные задания

По сопротивлению материалов

для студентов-заочников ускоренной формы обучения

Ростов-на-Дону

УДК 620.178.32 (076.5)

Методические указания и контрольные задания по сопротивлению материалов для студентов - заочников ускоренной формы обучения. – Ростов н/Д: Рост. гос. строит. ун-т, 2007. –36 с.

Даны условия заданий, теоретические положения и примеры расчета контрольной работы для студентов заочной ускоренной формы обучения.

Составители: канд. техн. наук, проф. И.А. Краснобаев

канд.физ.-мат. наук, доц. Г.П. Стрельников

канд. техн.наук, доц. Б.М. Языев

Редактор Н.Е.Гладких

Темплан 2007г., поз.129

Подписано в печать 30.01.07 Формат 60х84/16

Бумага писчая. Ризограф. Уч.-изд.л. 2,3.

Тираж 250 экз. Заказ

Редакционно-издательский центр

Ростовского государственного строительного университета.

344022, Ростов-на-Дону, ул. Социалистическая, 162.

С Ростовский государственный

строительный университет,2007

Указания о порядке выполнения контрольной работы

1.Студент выбирает данные из таблиц в соответствии со своим личным шифром –

номером зачетной книжки и первыми пятью буквами русского алфавита,

которые следует расположить под шифром, например,

шифр – 2 7 3 0 5

Буквы – а б в г д.

Из каждой вертикальной колонки любой таблицы, обозначенной внизу опреде-

ленной буквой, надо выбрать только одно число, стоящее в той горизонтальной

строке, номер которой совпадает с номером буквы. Например, в задаче 1 из

табл.1 выбираем: схема по рис.1 - 5; с = 2, 5м; q = 15кН/м; т.к. д = 5;

a = 2, 3м; F = 23кН; т.к. в = 3; b = 3м; m = 30кНм; т.к. г = 0.

2.В заголовке контрольной работы должны быть четко написаны: название дис-

циплины, фамилия, имя и отчество студента, наименование специальности,

учебный шифр и точный почтовый адрес.

3. Контрольная работа выполняется в тетради обычного формата с полями для

замечаний рецензента.

4.Перед решением каждой задачи необходимо выписать полностью ее условие с

числовыми данными, составить аккуратный эскиз в масштабе и указать на нем в

числах все величины, необходимые для расчета.

5.Решение должно сопровождаться объяснениями и чертежами.

6.После проверки контрольной работы студент должен исправить в ней

отмеченные ошибки и выполнить все сделанные ему указания. Исправления

должны быть вложены в соответствующие места рецензированной работы.

При решении контрольной работы рекомендуется использовать следующую литературу:

1. Дарков А.В., Шпиро Г.С. Сопротивление материалов.- М.,1975.

2. Писаренко Г.С. Сопротивление материалов.- Киев,1984.

3. Феодосьев И.И. Сопротивление материалов.- М.,1979.

ЗАДАЧИ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ

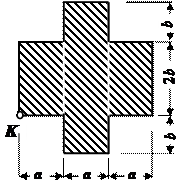
Задача 1

Абсолютно жесткий брус прикреплен к трем стержням при помощи шарниров (рис.1).Требуется:

1.Определить усилия в стержнях.

2.Считая, что все стержни круглого поперечного сечения, из условия прочности

при растяжении - сжатии подобрать диаметры этих стержней. Принять

допускаемое нормальное напряжение на сжатие [ s_с] = 100МПа, а на

растяжение - [ s_р] = 160МПа. Полученные по расчету диаметры стержней

округлить до четных или оканчивающихся на пять чисел (в миллиметрах).

3.Проверить прочность стержней.

Данные взять из табл. 1.

Таблица 1

№ строки	№ схемы по рис.1	a, м	b, м	c, м	F, кН	m, кНм	q, кН/м
		2,1	2,1	2,1
		2,2	2,2	2,2
		2,3	2,3	2,3
		2,4	2,4	2,4
		2,5	2,5	2,5
		2,6	2,6	2,6
		2,7	2,7	2,7
		2,8	2,8	2,8
		2,9	2,9	2,9
		3,0	3,0	3,0
	д	в	г	д	в	г	д

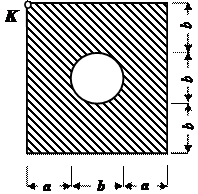
Задача 2

Для заданного поперечного сечения, состоящего из прокатных профилей (рис.2), требуется:

1.Определить положение центра тяжести. Построить центральные оси.

2.Найти величины осевых и центробежного моментов инерции относительно

центральных осей.

3. Определить направление главных центральных осей.

4. Найти величины осевых моментов инерции относительно главных центральных

осей.

5.Вычертить сечение в масштабе на миллиметровке формата А4 и указать на нем

все размеры в числах и все оси.

Данные взять из табл. 2.

Таблица 2

№ строки	№схемы сечений по рис.2	Дву-тавр	Швеллер	Пластина, мм×мм	Равнобокий уголок
				12×200	125×125×9
			18а	14×200	125×125×10
		18а		16×200	125×125×12
			20а	12×180	125×125×14
		20а		14×180	125×125×16
			22а	16×180	140×140×9
		22а		16×160	140×140×10
			24а	18×160	140×140×12
		24а		20×160	160×160×10
				24×140	160×160×11
	д	в	г	в	г

Рис.1

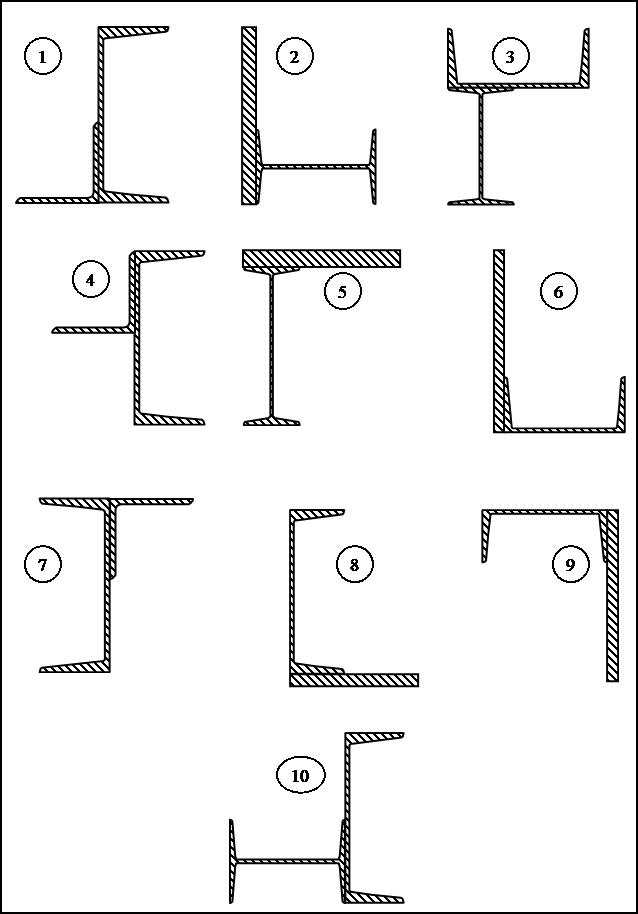Рис.2

Задача 3

Для заданных двух схем балок (рис.3) требуется:

1.Для каждого участка балки составить выражения поперечных сил (Q) и изгибающих моментов(M) , используя метод сечений. Построить их эпюры.

2.Определить опасное сечение по нормальным напряжениям.

3.Из условия прочности по методу допускаемых напряжений при изгибе

подобрать:

а) для схемы (а) деревянную балку круглого поперечного сечения, приняв

допускаемое нормальное напряжение [ s ] = 10МПа;

б) для схемы (б) стальную балку двутаврового поперечного сечения, приняв

допускаемое нормальное напряжение [ s ] = 160МПа.

4. Проверить прочность балок.

Данные взять из табл. 3.

Таблица 3

№ строки	№с схемы по рис.3	a, м	b, м	c, м	F, кН	m, кНм	q, кН/м
		2,1	2,1	2,1
		2,2	2,2	2,2
		2,3	2,3	2,3
		2,4	2,4	2,4
		2,5	2,5	2,5
		2,6	2,6	2,6
		2,7	2,7	2,7
		2,8	2,8	2,8
		2,9	2,9	2,9
		3,0	3,0	3,0
	д	в	г	д	в	г	д

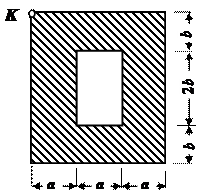
Задача 4

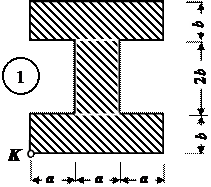
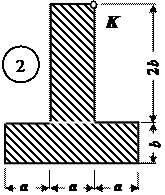
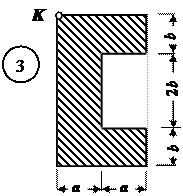
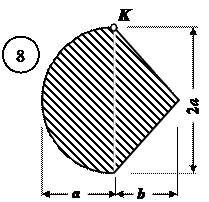
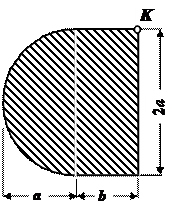
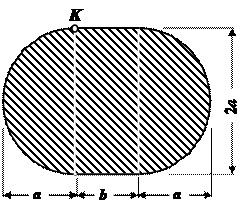
Чугунный короткий стержень, поперечное сечение которого изображено на рис.4, сжимается продольной силой F, приложенной в точке К.

Требуется:

1.Вычислить величины роверить прочность балок. наибольших растягивающих и сжимающих напряжений в

поперечном сечении, выразив величины этих напряжений через F.

2. Из условий прочности найти допускаемую нагрузку [F] при заданных

значениях допускаемых нормальных напряжений для чугуна на сжатие [ s_с] и

на растяжение [ s_р].

Данные взять из табл. 4.

Рис.3

Таблица 4

№ строки	№ схемы по рис.4	a, см	b, см	[ sс], МПа	[ sр], МПа
		2,1	2,1
		2,2	2,2
		2,3	2,3
		2,4	2,4
		2,5	2,5
		2,6	2,6
		2,7	2,7
		2,8	2,8
		2,9	2,9
		3,0	3,0
	д	в	г	в	г

Задача 5

Стальной стержень длиной l сжимается силой F. Требуется:

1. Из условия устойчивости подобрать размеры поперечного сечения при

допускаемом напряжении [s ]=160МПа. Расчет проводить последователь-

ными приближениями, предварительно задавшись величиной коэффициента

j = 0,5. Если гибкость стойки в первом приближении окажется меньше 50,

необходимо длину стойки увеличить в 2 раза, а при гибкости более 150 -

уменьшить в 2 раза. Проверить выполнение условия устойчивости.

2. Определить величину критической силы.

3. Найти значения допускаемой нагрузки и коэффициента запаса устойчивости.

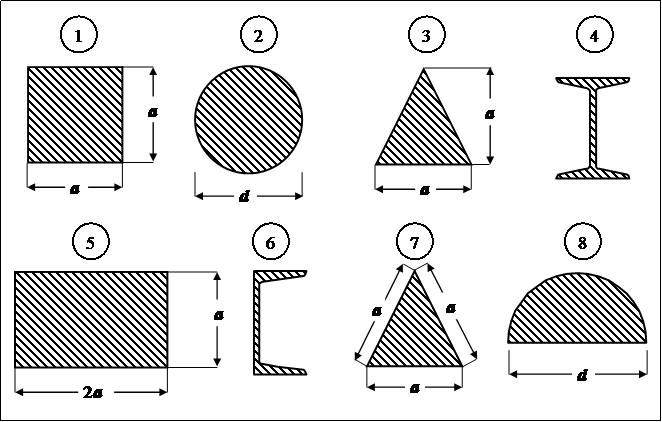
Данные взять из табл. 5.

Таблица 5

№ строки	№ схемы закрепления концов стержня по рис.5	Формы сечения стержня по рис.6	F, кН	l, м
				2,1
				2,2
				2,3
				2,4
				2,5
				2,6
				2,7
				2,8
				2,9
				3,0
	д	в	г	г

Рис.4

Схемы закрепления концов стержня

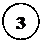
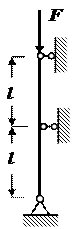
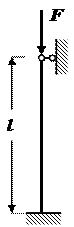
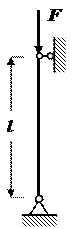
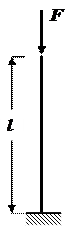
Рис.5

Формы сечения стержня

Рис.6

Задача 1

Абсолютно жесткий брус прикреплен к трем стержням при помощи шарниров (рис.7).Требуется:

1.Определить усилия в стержнях.

2.Считая, что все стержни круглого поперечного сечения, из условия прочности

при растяжении - сжатии подобрать диаметры этих стержней. Принять

допускаемое нормальное напряжение на сжатие [ s_с] = 100МПа, а на

растяжение - [ s_р] = 160МПа. Полученные по расчету диаметры стержней

округлить до четных или оканчивающихся на пять чисел (в миллиметрах).

3.Проверить прочность стержней.

Исходные данные:

a=2, 4 м; b=2 м; c=3 м;

m=32 кНм; F=30 кН; q=10 кН/м;

[ s_р] = 160МПа=160 ;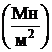

[ s_с] = 100МПа=100 .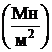

Рис.7

Решение

Рис.8

Проверка прочности стержней

Фактическая площадь поперечного сечения первого и второго стержней

,

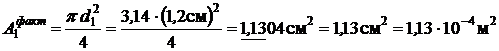тогда рабочее нормальное напряжение

.

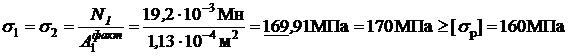Из полученного результата устанавливаем, что стержни перегружены. Определяем величину перегрузки

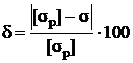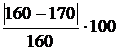% = % = 6,55 % > 5 % .

Замечание. По методу расчета по допускаемым напряжениям возможна

перегрузка стержней в пределах 5 %.

Увеличиваем диаметры первого и второго стержней d₁ = d₂ = 1,4 см.

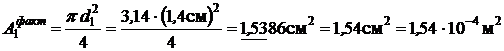, тогда рабочее нормальное напряжение

.

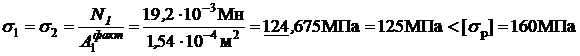Условие прочности выполняется.

Окончательно принимаем d₁ = d₂ = 1,4 см.

Фактическая площадь поперечного сечения третьего стержня

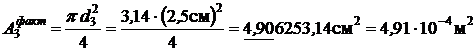, тогда рабочее нормальное напряжение

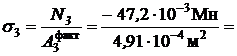- 96, 130МПа= - 96, 1МПа.

│s₃│= 96, 1МПа < [ s_с] = 100МПа.

Условие прочности выполняется. Окончательно принимаем d₃ = 2, 5 см.

Задача 2

Для заданного поперечного сечения, состоящего из прокатных профилей (рис.9), требуется:

1.Определить положение центра тяжести. Построить централь-

ные оси.

2.Найти величины осевых и центробежного моментов инерции

относительно центральных осей.

3. Определить направление главных центральных осей.

4. Найти величины осевых моментов инерции относительно

главных центральных осей.

5.Вычертить сечение в масштабе на миллиметровке формата А4

и указать на нем все размеры в числах и все оси.

Рис.9

Исходные данные: пластина - 200 ´ 20; равнобокий уголок - 160´160´12.

Решение

Будем считать, что пластина - фигура I, а равнополочный уголок -фи-гура II. Используя справочные таблицы, выписываем данные для каждой фигуры.

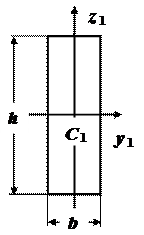Фигура I- пластина 200´20

b=20 мм =2см;h=200 мм =20 см;

A₁=b h= 2∙20см²=40 см²;

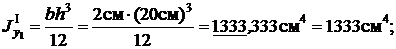
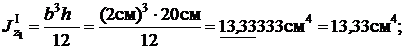
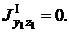
Фигура II - равнополочный уголок 160´160´12

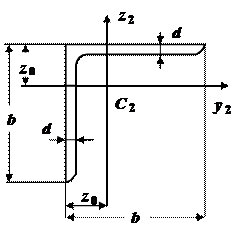b=160 мм =16см;

d=12мм =1, 2 см;

A₂=37, 4 см²;

z₀=4, 39см;

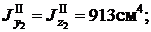
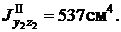
Здесь и в дальнейшем A_1, A₂ - соответственно площади первой и второй фигур, A - площадь составной фигуры (общая площадь). Верхние индексы I , II у моментов инерции соответствуют номерам фигур, их отсутствие означает, что определяется момент инерции всего сечения. Например, 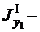момент инерции первой фигуры относительно оси y₁; центробежный момент инерции второй фигуры относительно осей y₂, z₂.

Замечание. В справочных таблицах значения центробежного момента инерции

уголка приводятся без учета знака. Знак центробежного момента

инерции можно выбрать в соответствии с рис.10.

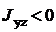
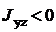
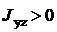
Рис.10

Используя приведенные выше справочные данные, вычерчиваем сечение в масштабе с указанием всех осей и необходимых размеров в сантиметрах (рис.11). На рис.11 в рамках показаны размеры, взятые из справочных данных, остальные получены в ходе расчета.

Главных центральных осей

Моменты инерции относительно главных центральных осей вычисляются по следующим формулам:

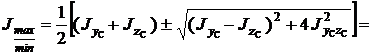
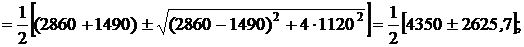
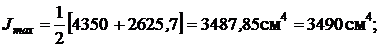
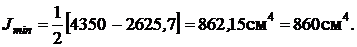
Так как , то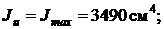

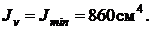
Наибольший из моментов инерции при повороте осей возрастает, достигая максимального значения, а меньший момент инерции убывает, достигая минимального значения, при этом сумма осевых моментов инерции относительно двух взаимно перпендикулярных осей остается постоянной, т.е.

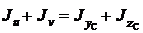=const.

Используем последнее соотношение в качестве проверки

= = .

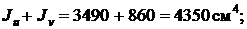
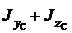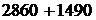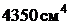Задача 3

Для заданных двух схем балок (рис.12,15) требуется:

1.Для каждого участка балки составить выражения поперечных сил (Q) и изги-

бающих моментов(M) , используя метод сечений. Построить их эпюры.

2.Определить опасное сечение по нормальным напряжениям.

3.Из условия прочности по методу допускаемых напряжений при изгибе

подобрать:

а) для схемы (а) деревянную балку круглого поперечного сечения, приняв

допускаемое нормальное напряжение [ s ] = 10МПа;

б) для схемы (б) стальную балку двутаврового поперечного сечения, приняв

допускаемое нормальное напряжение [ s ] = 160МПа.

4. Проверить прочность балок.

Схема а)

Исходные данные:

a=2 м; b=2 м; q=10 кН/м;

m=8 кНм; F=15 кН;

[s ] = 10МПа=10 .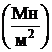

Рис.12

Решение

1.Построение эпюр поперечной силы Q и изгибающего момента M

Разбиваем расчетную схему балки на участки. Границами участка являются точки приложения сосредоточенных сил, сосредоточенных моментов, точки начала и конца распределенной нагрузки. В нашем примере балка имеет два участка, которые пронумеруем справа налево (рис. 14). Для определения внутренних усилий необходимо на каждом участке использовать метод сечений, который сводится к следующему.

1. Проводим поперечное сечение, которое разбивает балку на две части;

2. Выбираем ту часть балки, на которую действуют известные нагрузки (левую от сечения или правую);

3. Составляем выражения для поперечной силы Q и изгибающего момента M,

при этом руководствуемся определением и правилом знаков.

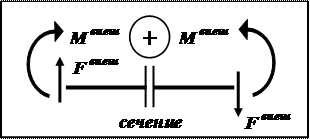
Определение. Поперечная сила Q – это внутренняя сила, численно равная

алгебраической сумме всех внешних сил, действующих по одну

сторону от сечения перпендикулярно оси балки.

Определение. Изгибающий момент M –это внутренний момент, численно равный

алгебраической сумме моментов всех внешних сил, действующих

по одну сторону от сечения относительно центра тяжести попереч-

ного сечения.

Правило знаков. Поперечная сила в поперечном сечении балки положительная

(Q>0), если внешние силы (F^внеш) направлены так, как показано на рис.13.

Изгибающий момент в поперечном сечении балки положителен(M >0), если

моменты внешних сил (M^внеш) направлены так, как показано на рис.13.

Поперечная сила и изгибающий момент отрицательны, если направления внешних сил и моментов внешних сил противоположны направлениям, указанным на рис.13.

Рис.13

Проводим сечение на первом участке и рассматриваем правую от сечения часть балки (рис.14), т.к. слева от сечения опорные реакции неизвестны.

I участок 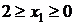(сечение перемещается от правой до левой границы).

Составляем выражение для поперечной силы с учетом правила знаков справа от сечения

Q(x₁)= - F + qx₁= - 15 + 10x₁(уравнение прямой линии).

Здесь qx₁ - равнодействующая сила распределенной нагрузки q, расположенная справа от сечения посредине участка длиной x₁.

Определяем значения Q на границах участка

Q(0)= - 15 + 10 · 0= - 15 кН (значение на правой границе участка);

Q(2)= -15 + 10 ·2=5 кН(значение на левой границе участка).

Поскольку поперечная сила меняет знак в пределах участка, определяем координату, при которой она обращается в нуль (в этом сечении изгибающий момент принимает экстремальное значение):

Q(x₀)= - 15 + 10x₀=0; x₀=15/10=1,5 м.

Составляем выражение для изгибающего момента с учетом правила знаков справа от сечения

M(x₁) = 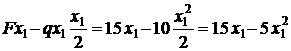(уравнение квадратичной параболы).

Определяем значения M на границах участка и в найденной точке x₀

M(0)=0 (значение на правой границе участка) ;

M(1,5)= 1,5·(15 – 5·1,5)=11,25 кНм=11,3 кНм(значениев точке x₀);

M(2)=2·(15 – 5·2)=10 кНм (значение на левой границе участка).

II участок 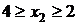(сечение перемещается от правой до левой границы).

Составляем выражение для поперечной силы с учетом правила знаков справа от сечения

Q(x₂)= - F + q·2= - 15 + 10·2= 5 кН (прямая линия параллельная оси x).

Составляем выражение для изгибающего момента с учетом правила знаков справа от сечения

M(x₂) = 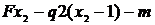= 15x₂ - 20 (x₂-1) – 8 = - 5x₂ + 12 (уравнение прямой).

M(2)= - 5 ·2 + 12= 2 кНм (значение на правой границе);

M(4)= - 5 ·4 + 12= - 8 кНм (значение на левой границе).

Проверка прочности балки

Проверяем выполнение условия прочности. С этой целью вычисляем фактический момент сопротивления

= =

Находим максимальное нормальное напряжение 10 =10 МПа=[s ].

Условие прочности выполняется, окончательно принимаем d =22, 6см.

Схема б) Исходные данные:

a=2 м; b=3 м; c=1 м; q=15 кН/м;

m=20 кНм; F=30 кН;

[s ] = 160МПа=160 .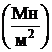

Рис.15 Решение

1.Определение поперечных сил (Q) и изгибающих моментов(M).

Построение их эпюр

а) нахождение опорных реакций

Обозначим опоры буквами A и B соответственно и заменим их действие опорными реакциями (рис.17). Составляем три уравнения

статики (равновесия), используя правило знаков, показанное на рис.16.

Сумма проекций всех сил на горизонтальную ось x

; .

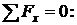
Сумма моментов всех сил относительно точки A

m - q·3(2+1, 5) + R_B·5- F·6 =0;

20- 15·3·3, 5 + R_B·5- 30·6 =0; Рис.16

20- 157, 5 + R_B·5- 180 =0;

-317, 5 + R_B·5=0; R_B= 63,5 кН.

Сумма моментов всех сил относительно точки B

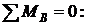- R_A·5+ m + q·3·1, 5- F·1 =0;

- R_A·5 + 20 +15·4, 5 -30 =0;

- R_A·5 + 20 +67, 5 - 30 =0;

-R_A·5 - 57, 5 =0; R_A= 11, 5 кН.

Допускаемых напряжений

Из условия прочности (2) определяем требуемую величину момента сопротивления

.

По сортаменту прокатной стали для двутаврового сечения ближайшим к является значение момента сопротивления =184 см³ (двутавр №20).

Проверка прочности балки

Для двутавра №20 184см³=184·10^{-6 м3};

проверяем выполнение условия прочности:

163,049 МПа=163 МПа> [s ] =160 МПа.

На основании полученного результата устанавливаем, что балка перегружена. Определяем величину перегрузки

×100 % %=1,88 % <5%.

Условие 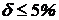выполняется, поэтому окончательно выбираем двутавр №20.

Задача 4

Чугунный короткий стержень, поперечное сечение которого изображено на рис.19, сжимается продольной силой F, приложенной в точке К. Требуется:

1.Вычислить величины роверить прочность балок. наибольших растягивающих и сжимающих напряжений в

поперечном сечении, выразив величины этих напряжений через F.

2. Из условий прочности найти допускаемую нагрузку [F] при заданных

значениях допускаемых нормальных напряжений для чугуна на сжатие [ s_с] и

на растяжение [ s_р].

Исходные данные:

a=4 см; b=6 см;

[ s_с] = 160МПа=160 ;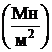

[ s_р] = 40МПа=40 .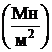

Рис.19

Решение

Будем считать, что пластина - фигура I, а полукруг -фигура II. Используя справочные таблицы, выписываем данные для каждой фигуры.

Фигура I- прямоугольник 4см´6 см

b=4см;h=6 см; A₁= b h= 4∙6см²=24 см²;

Фигура II - полукруг, диаметра d=2b=12см

z₀=0, 212d =0, 212∙12см=2, 544=2, 54см;

.

Нормальные напряжения в случае внецентренного сжатия находятся по формуле:

. (5)

В этой формуле:s - величина нормального напряжения в любой точке сечения c координатами y, z;

F- величина внецентренной силы, приложенной в точке K; A - площадь поперечного сечения;

y_K, z_K - координаты точки приложения силы, взятые относительно главных

центральных осей заданного сечения;

, - квадраты радиусов инерции, которые определяются по формулам:

, .

Используя приведенные выше справочные данные, вычерчиваем сечение в масштабе с указанием всех осей и необходимых размеров в сантиметрах (рис.20). На рис.20 в рамках показаны размеры, взятые из справочных данных, остальные получены в ходе расчета.

Центральных осей

Составная фигура имеет ось симметрии y(рис.20), которая является главной центральной осью. Вторую главную центральную ось проведем после опреде-ления положения центра тяжести, который находится на оси симметрии y.

Определяем координаты точек С₁ и С₂ относительно системы z₁C₁y₁.

Точка С₁: 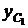=0. Точка С₂ : .

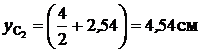Общая площадь фигуры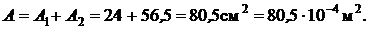

Координата центра тяжести по оси y

.

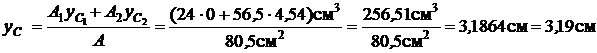Проводим через точку С главную центральную ось z.

Теперь y, z - основная система координат (рис.20).

б) определение моментов инерции и квадратов радиусов инерции

Сжимающих напряжений

Определение. Опасными точками поперечного сечения являются точки, в кото-

рых возникают наибольшие напряжения.

Опасные -это точки, наиболее удаленные от нейтральной линии.

На рис.20 - это точки K(точка приложения силы) и D.

Определяем их координаты.

Точка K: y_K= -5, 19см; z_K =3см (см. рис.20).

Точка D: y_D=4, 3см; z_D =-2, 5см (см. рис.20).

Координаты точки D найдены графически, т.е. измерены расстояния от точки C до точки D по оси y и оси z. Полученный результат умножили на масштабный коэффициент (чертеж поперечного сечения должен быть выполнен в масштабе).

Нормальные напряжения в точке K

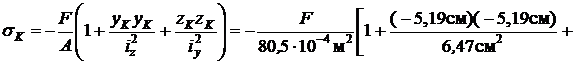
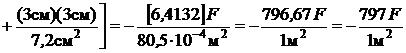(сжатие).

Нормальные напряжения в точке D

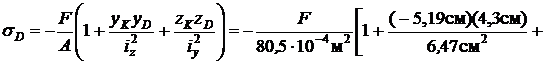
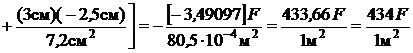(растяжение).

2. Определение допускаемой нагрузки [F] из условий прочности на растяжение и сжатие

Условие прочности на сжатие имеет следующий вид: .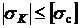

;

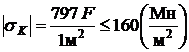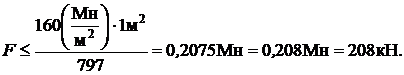
Условие прочности на растяжение имеет следующий вид: .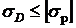

;

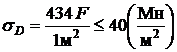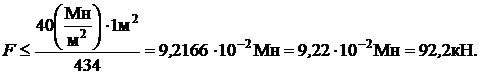
Из двух неравенств и 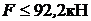выбираем меньшее значение силы.

Допускаемая нагрузка .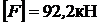

Задача 5

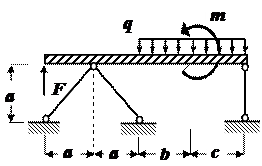
Стальной стержень длиной l сжимается силой F (рис.21). Требуется:

1. Из условия устойчивости подобрать размеры поперечного сечения при

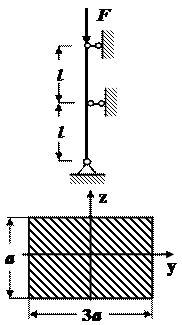допускаемом напряжении [s ]=160МПа. Расчет проводить

последовательными приближениями, предварительно

задавшись величиной коэффициента j = 0,5. Если гибкость

стойки в первом приближении окажется меньше 50, необхо-

димо длину стойки увеличить в 2 раза, а при гибкости более

150- уменьшить в 2 раза. Проверить выполнение условия

устойчивости.

2. Определить величину критической силы.

3. Найти значения допускаемой нагрузки и коэффициента

запаса устойчивости.

Исходные данные:

l=2 м =200см; F=200 кН=0, 2 МН;

[ s ] = 160МПа=160 .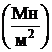

Рис.21 Решение

Условие устойчивости при центральном сжатии по методу допускаемых

напряжений имеет вид:

s 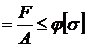, (6)

где s - нормальное напряжение;F - величина сжимающей силы;

A- площадь поперечного сечения стержня (рис.21);

[s] - допускаемое нормальное напряжение на центральное сжатие;

j - коэффициент продольного изгиба центрально-сжатых элементов (коэффици-ент понижения основного допускаемого напряжения).

Применяя условие устойчивости, можно выполнить три вида расчета:

1.Проектный расчет. По заданной нагрузке F