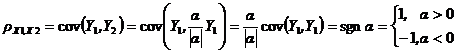Лекция 16. числовые характеристики меры связи случайных величин

Между случайными величинами может существовать функциональная взаимосвязь. Однако связь может быть и такого рода, что закон распределения одной случайной величины изменяется в зависимости от значений, принимаемых другой случайной величиной. Такую зависимость называют стохастической или вероятностной. Одной из характеристик стохастической взаимосвязи двух случайных величин является ковариация случайных величин.

Определение 1. Ковариацией случайных величин Х_i и Х_j называется число, равное математическому ожиданию произведения отклонений случайных величин Х_i и X_j от своих математических ожиданий

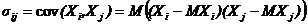. (1)

При вычислении используется формула

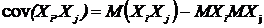. (2)

Покажем справедливость этого утверждения:

s_ij=M((X_i – MX_j) (X_j – MX_j)) = M(Х_i Х_j – X_i MX_j – MX_j X_j + MX_j MX_j) =M(Х_i Х_j) – MX_j MX_j – MX_j MX_j + MX_j MX_j = M(Х_i Х_j) – MX_j MX_j.

Если Х_i и Х_j независимы, то ковариация равна нулю, так как М(Х_i , X_j) = МХ_iМX_j. Обратное утверждение неверно. Если ковариация не равна нулю, то случайные величины зависимы.

Рассмотрим некоторые свойства ковариации:

1) cov(X, Y) = cov(Y, X);

2) cov(X, X) = DX;

3) cov(X + c, Y + c) = cov(X, Y);

4) cov(Xc₁ + Yc₂, Z) = с₁cov(X, Z) + с₂cov(Y, Z), с₁, c₂ – const.

Пусть задан случайный вектор X = (X₁, X_2,…, X_n).

Определение 2.Ковариационной матрицей случайного вектора X = (X₁, X_2,…, X_n) назвается матрица å, элементами которой являются ковариации :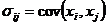

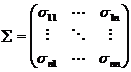(3)

Очевидно, что матрица симметричная, а диагональные элементы равны дисперсиям случайных величин Х_i, s_ii = DX_i, i = 1,2,…

Определение 3.Определитель ковариационной матрицы å называется обобщенной дисперсией случайного вектора, который характеризует меру рассеивания случайного n-мерного вектора.

В теории вероятностей и её приложениях часто появляется необходимость перейти с помощью линейного преобразования к новым случайным величинам, X = (X₁, X_{2, …,} X_n)→ Y = (Y₁, Y_{2, …,}Y_m), при этом .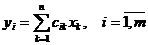

Обозначим через С = {c_ij} матрицу коэффициентов линейного преобразования, через Х и Y – векторы столбцы 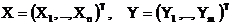, тогда линейное преобразование можно записать как Y = CX.

Теорема 1. Если для случайного вектора Х существует ковариационная матрица Σ, то при любых значениях элементов матрицы С существует ковариационная матрица Н для случайного вектора Y = CX, причём .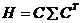

Доказательство. Пусть ; ;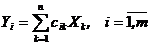

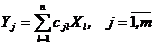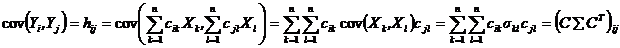Следствие 1.

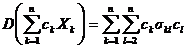. (4)

Доказательство. Пусть .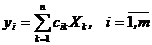

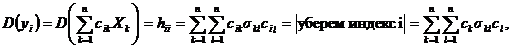
например, если n = 2, то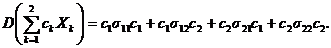

Следствие 2. Если в формуле из следствия 1 предположить, что 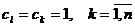, то

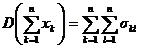. (5)

Следствие 3. Если в формуле из следствия 1 предположить, что n = 1, то

.

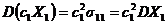Следствие 4. Если в формуле из следствия 2 предположить, что n = 2, то

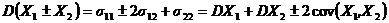(6)

Следствие 5. Если Х_k независимы, то в матрице å все недиагональные элементы равны нулю, а диагональные элементы равны дисперсиям соответствующих элементов Х_к, поэтому, учитывая следствие 2, имеем

.

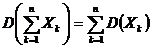Пример 1. Вычислим ковариационную матрицу å случайного вектора Z = (X,Y), дисперсии случайных величин U₁ = X+Y, U₂ = 2X–3Y и ковариационную матрицу Н вектора U = (U₁, U₂). Распределение случайного вектора Z задано в таблице.

	J					pi·
I	Yj Xi		0,1	0,2	0,3
		0,2	0,1	0,05	0,05	0,4
			0,15	0,15	0,15	0,1
				0,1	0,1	0,2
p·j		0,2	0,25	0,3	0,25

МХ = 5·0,4+6·0,4+7·0,2 = 5,8; М Y = 0·0,2+0,1·0,25+0,2·0,3+0,3·0,25 = 0,16;

М(Х,Y)= 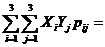5·0·0,2+5·0,1·0,1+5·0,05·0,2+5·0,05·0,3+6·0·0+6·0,1·0,1+6·0,15·0,2+6·0,1·0,3+7·0·0+7·0·0,1+7·0,1·0,2+7·0,1·0,3 = 0,975.

Матрица å имеет вид å= 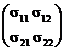, где s_{11 =} cov(X,X), s_{12 =} cov(X,Y), s_{21 =} cov(Y,X), s_{22 =} cov(Y,Y);

s₁₂ = s₂₁ = M(XY)-MXMY = 0,975-5,8·0,16 = 0,047;

s₁₁ = cov(X,X) = DX=MX² – (MX)² = (5²·0,4+6²·0,4+7²·0,2) – 5,8² = 0,56;

s_{22 =} cov(Y,Y) = DY = MY² – (MY)² = (0·0,2+0,1²·0,25+0,2²·0,3+0,3²·0,25) – 0,16² = 0,0114.

Следовательно, å = .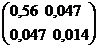

Найдем DU₁ = D(X + Y)= 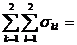0,56 + 0,047 + 0,047 + 0,0114 = 0,6654;

DU₂ = D(2X – 3Y) = 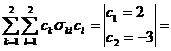c₁s₁₁c₁ + c₁s₁₂c₂ + c₂s₂₁c₁+ c₂s₂₂c₂ = 2·2·0,56 – 2·3·0,047 – 3·2·0,047 + 3·3·0,0114 = 1,778.

Ковариационную матрицу вектора U = (U₁, U₂) можно определить по формуле

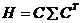, где С = 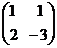, тогда Н = .

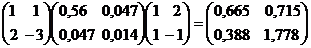Из свойств ковариации следует, что значение ковариации линейно зависит от масштаба измерения случайных величин. Если изменить масштаб, то изменится и значение ковариации, например, если от случайной величины Х₂ перейти к новой случайной величине Y₂ = с₂ Х₂, то cov(X₁, Y₂) = c₂cov(X₁,X₂). Это свойство ковариации ограничивает возможности его применения. Для получения характеристики взаимосвязи случайных величин, которая бы не зависела от преобразования случайных величин вида Y = аX + в, перейдем к рассмотрению нормированных случайных величин.

Пусть Х₁, Х₂ – случайные величины. Тогда им соответствуют нормированные величины: , .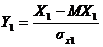

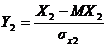Найдем ковариацию Y₁,Y₂

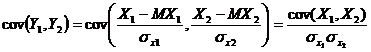– коэффициент корреляции случайных величин.

Определение 4.Коэффициентом корреляции случайных величин Х₁, Х₂ называется число r_{х1, х2} равное ковариации нормированных случайных величин Х₁, Х₂, т.е.

r_{х1, х2} = .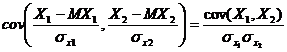

Для независимых случайных величин r_х1,х2 = 0, так как cov(X₁,X₂) = 0. Обратное утверждение не верно (оно справедливо только для нормально распределенных случайных величин), но если r_х1,х2 ¹ 0, то случайные величины Х₁, Х₂ – зависимы.

Определение 5. Случайные величины называются некоррелированными, еслиr_{х1, х2} = 0.

При изменении масштаба случайной величины значение корреляции не изменяется.

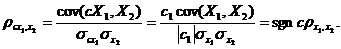
Рассмотрим пример, который показывает, что из равенства нулю коэффициента корреляции не следует независимость случайных величин.

Пусть 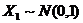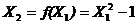, тогда

.

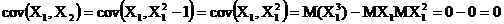
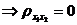Теорема 2. Абсолютное значение коэффициента корреляции меньше либо равно 1: .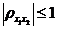

Доказательство. Пусть заданы случайные величины Х₁, Х₂. Рассмотрим нормированные случайные величины 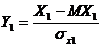, 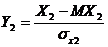. Тогда в соответствии с формулой (6)

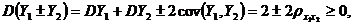следовательно, .

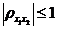Теорема 3. 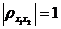, тогда и только тогда, когда X_1, X₂ связаны линейной зависимостью, т.е. Х₂ = aХ₁ + b, причем если a > 0, то 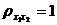; если a< 0, то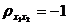

Доказательство.

I. Пусть 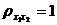. Покажем, что Х₁ и Х₂линейно зависимы.

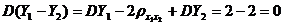, т.е.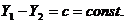

Покажем, что с = 0.

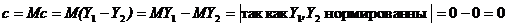, т.е. ,

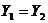следовательно 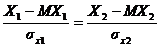. Запишем последнее равенство в виде

,

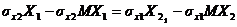выразим из него Х₂:

,

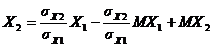обозначив множитель при первом слагаемом a, а два других через b, получим, что

Х₂ = aХ₁ + b.

Аналогичный результат можно получить в предположении, что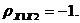

II. Пусть Х₂ = aХ₁ + b, покажем, что .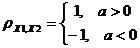

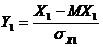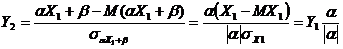, , следовательно