Лекция 1. теории вероятностей. история возникновения. классическое определение вероятности

А.А. Халафян

ТЕОРИЯ ВЕРОЯТНОСТЕЙ

И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

тексты лекций

Краснодар 2008

Статистическое определение вероятности

Существует большой класс событий, вероятности которых не могут быть вычислены с помощью классического определения. В первую очередь это события с неравновозможными исходами (например, игральная кость «нечестная», монета сплющена и т.д.). В таких случаях может помочь статистическое определение вероятности, основанное на подсчете частоты наступления события в испытаниях.

Определение 2.Статистической вероятностьюнаступления события А называется относительная частота появления этого события в n произведенных испытаниях [4], т.е.

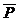(А) = W(A) = m/n,

где 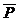(А) – статистическое определение вероятности; W(A) – относительная частота; n – количество произведенных испытаний; m – число испытаний, в которых событие А появилось. Заметим, что статистическая вероятность является опытной, экспериментальной характеристикой.

Причем при n → ∞, 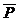(А) → P(А), так, например, в опытах Бюффона (XVIII в.) относительная частота появления герба при 4040 подбрасываниях монеты, оказалось 0,5069, в опытах Пирсона (XIX в.) при 23000 подбрасываниях – 0,5005.

Геометрическое определение вероятности

Еще один недостаток классического определения, ограничивающий его применение, является то, что оно предполагает конечное число возможных исходов. В некоторых случаях этот недостаток можно устранить, используя геометрическое определение вероятности. Пусть, например, плоская фигура g составляет часть плоской фигуры G (рис.3).

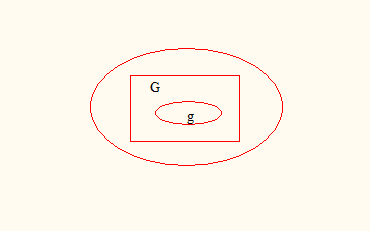
Рис.3

На фигуру G наудачу бросается точка. Это означает, что все точки области G «равноправны», в отношении попадания туда брошенной случайной точки. Полагая, что вероятность события А – попадание брошенной точки на g пропорциональна площади этой фигуры S_g и не зависит ни от ее расположения относительно области G, ни от формы g, найдем

Р(А) = S_g/S_G

где S_G – площадь области G. Но так как области g и G могут быть одномерны- ми, двухмерными, трехмерными и многомерными, то, обозначив меру области черезmeas, можно дать более общее определение геометрической вероятности

P = measg / measG.

Доказательство.

Р(В/А) = Р(ВÇА)/Р(А) = Р(АÇВ)/Р(А) = {P(a/b)Р(В)}/Р(А) = {Р(А)Р(В)}/Р(А) = Р(В).

Из определения 4 вытекают формулы умножения вероятностей для зависимых и независимых событий.

Следствие 1. Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились:

P(A₁A₂… A_n) = P(A₁)P_A1(A₂)P_A1A2(A₃)… P_{A1A2… An-1}(A_n).

Определение 6. События A_1, A_2, …, A_n независимы в совокупности, если независимы любые два из них и независимы любое из этих событий и любые комбинации (произведения) остальных событий.

Следствие 2. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:

P(A₁A₂… A_n) = P(A₁)P(A₂)… P(A_n).

Доказательство.

P(A₁A₂… A_n) = P(A₁·A₂… A_n) = P(A₁)P(A₂… A_n).=…= P(A₁)P(A₂)… P(A_n).

Определение 7. Событие А₁,А₂,… А_n образуют полную группу событий, если они попарно несовместны (А_i∩А_j = Ø, для любого i ≠ j)и в совокупности образуют Ω, т.е. .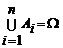

Теорема 2.Если события А_1,A₂,… А_n образуют полную группу событий, Р(А_i) > 0 (так как не будет определено P(B/A_i)), то вероятность некоторого события B Î S определяется, как сумма произведений безусловных вероятностей наступления события А_i на условные вероятности наступления события B, т.е.

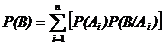.(1)

Доказательство. Так как события А_i попарно несовместны, то их пересечение с событием B также попарно несовместны, т.е. B∩А_i и B∩А_j – несовместны при i ¹ j. Используя свойство дистрибутивности ((ÈА_i)ÇВ = È(А_iÇВ)), событие B можно представить как 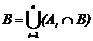. Воспользуемся аксиомой сложения 3 и формулой умножения вероятностей, получим

.

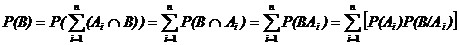Формула (1) называется формула полной вероятности.

Из формулы полной вероятности легко получить формулу Байеса, при дополнительном предположении, что P(B)>0

,

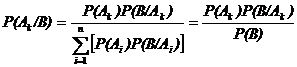где k = 1, 2, …, n.

Доказательство.P(А_k/B) = P(А_k ∩ B)/P(B)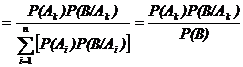

Вероятности событий P(А_i ), i =1, 2, …, n называются априорными вероятностями, т.е. вероятностями событий до выполнения опыта, а условные вероятности этих событий P(А_k/B), называются апостериорными вероятностями, т.е. уточненными в результате опыта, исходом которого послужило появление события В.

Задача. В торговую фирму поступили сотовые телефоны последних моделей от трех производителей Alcatel, Siemens, Motorola в соотношении 1 : 4 : 5. Практика показала, что телефоны, поступившие от 1-го, 2-го, 3-го производителя, не потребуют ремонта в течение гарантийного срока соответственно в 98 %, 88 % и 92 % случаев. Найти вероятность того, что поступивший в продажу телефон не потребует ремонта в течение гарантийного срока, проданный телефон потребовал ремонта в течение гарантийного срока, от какого производителя вероятнее всего поступил телефон.

Пример 1.

Очки на гранях игральной кости
Вероятности	1/6	1/6	1/6	1/6	1/6	1/6

Пример 2.

Монета	Орёл	Решка
Вероятность	0,5	0,5

Определение 1. Случайной величиной вероятностного пространства {Ω, S, P} называется любая функция X(w), определенная для wÎΩ, и такая, что для всех действительных х ( 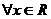) множество {w: X(w) < x}принадлежит полю S. Другими словами для любого такого события w определена вероятность P(X(w) < x) = P(X < x).

Случайные величины будем обозначать прописными латинскими буквами X, Y, Z, …, а значения случайных величин – строчными латинскими буквами x, y, z...

Определение 2. Случайная величина X называется дискретной, если она принимает значения только из некоторого дискретного множества. Другими словами, существует конечное или счетное число значений x₁, x₂, …, таких, что P(X = x_i) = р_i ³ 0, i = 1, 2…, причем å p_i = 1.

Если известны значения случайной величины и соответствующие им вероятности, то говорят, что определен закон распределения дискретной случайной величины.

Если составлена таблица, в верхней части которой располагаются значения случайных величин, а в нижней части соответствующие им вероятности, то получим ряд распределения случайной величины, который задает закон распределения дискретной случайной величины.

Пример 3. Составим ряд распределения выпадения герба при 2 подбрасываниях монеты. Возможные исходы – ГГ, ГР, РГ, РР. Из возможных исходов видно, что герб может выпасть 0, 1 и 2 раза, с соответствующими вероятностями – ¼, ½, ¼. Тогда ряд распределения примет вид

X_i :0 1 2

р_i :¼ ½ ¼

Определение 3.Функцией распределения случайной величины X называется функция F(x), зависящая от х Î R и принимающая значение, равное вероятности события w, что X < x, т.е.,F(x) = P{w: X(w) < x } = P(X < x ).

Из определения следует, что любая случайная величина имеет функцию распределения.

Равномерное распределение

Определение 1. Случайная величина Х, принимающая значения 1, 2, …, n, имеет равномерное распределение, если P_m = P(Х = m) = 1/n,

m = 1, …, n.

Очевидно, что .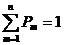

Рассмотрим следующую задачу.В урне имеется N шаров, из них M шаров белого цвета. Наудачу извлекается n шаров. Найти вероятность того, что среди извлечённых будет m белых шаров.

Нетрудно видеть, что .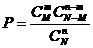

Распределение Пуассона

Определение 4. Случайная величина Х имеет распределение Пуассона с параметром l, если 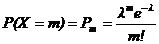, m = 0, 1, …

Покажем, что Σp_m = 1. .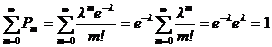

Биномиальное распределение

Определение 5.Случайная величина X имеет биномиальное распределение, если 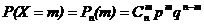, m = 0, 1, …, n,

где n – число испытаний по схеме Бернулли, m – число успехов, р – вероятность успеха в единичном исходе, q = 1–p.

Распределение Бернулли

Определение 6.Случайная величина Х имеет распределение Бернулли, если P(Х = m) = P_m = p^mq^n-m, m = 0, 1, …, n.

При больших m и n становится проблематичным вычисление по формуле Бернулли. Поэтому в ряде случаев удается заменить формулу Бернулли подходящей приближенной асимптотической формулой. Так если n – велико, а р мало, то .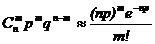

Теорема Пуассона. Если n ® ¥, а p ® 0, так что np ® l, то .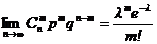

Доказательство. Обозначим l_n = np, по условию теоремы 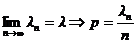, тогда

.

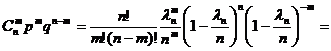
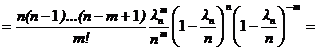
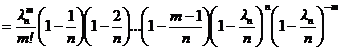При n ® ¥, l_n^m ® l^m,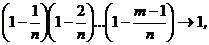

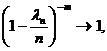
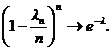
Отсюда получаем утверждение теоремы. Р_n(m) ® 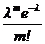при n ® ¥.

Формула Пуассона хорошо приближает формулу Бернулли, если npq £ 9. Если же произведение npq велико, то для вычисления Р_n(m) используют локальную теорему Муавра–Лапласа.

Локальная теорема Муавра – Лапласа.Пусть pÎ(0;1) постоянно, величина 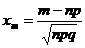равномерно ограничена, т.е. $с, |x_m|<с. Тогда

,

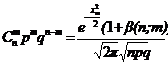где b(n;m) – бесконечно малая величина, причем .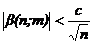

Из условий теоремы следует, что ,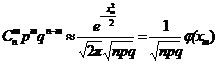

где , .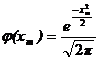

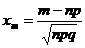Для вычисления Р_n(m) по формуле, приведенной рнее, используют таблицы функции

.

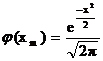Задача 1. В магазин одежды один за другим входят трое посетителей. По оценкам менеджера, вероятность того, что вошедший посетитель совершит покупку, равна 0,3. Составить ряд числа посетителей, совершивших покупку.

Решение.

xi
рi	0,343	0,441	0,189	0,027

Задача 2. Вероятность поломки произвольного компьютера равна 0,01. Построить ряд распределения числа вышедших из строя компьютеров с общим числом 25.

Решение.

xi								…
рi (Пуассон)	0,778	0,196	0,024	0,002	0,000	0,000	0,000	0,000	0,000
рi (Бернулли)	0,779	0,195	0,022	0,001	0,000	0,000	0,000	0,000	0,000

Задача 3. Автомобили поступают в торговый салон партиями по 10 шт. В салоне подвергаются контролю качества и безопасности только 5 из 10 поступивших автомобилей. Обычно 2 из 10 поступивших машин не удовлетворяют стандартам качества и безопасности. Чему равна вероятность, что хотя бы одна из 5 проверяемых машин будет забракована.

Решение. Р = Р₍₁₎ + Р₍₂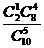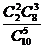₎ = + =0,5556 + 0,2222 = 0,7778

Доказательство.

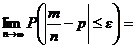
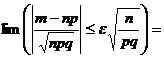
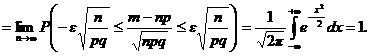
Задача 1. Вероятность того, что случайно выбранный прибор нуждается в дополнительной настройке, равна 0,05. Если при выборочной проверке партии приборов обнаруживается, что не менее 6 % отобранных приборов нуждаются в регулировке, то вся партия возвращается для доработки. Определить вероятность того, что партия будет возвращена, если для контроля из партии выбрано 500 приборов.

Решение.Партия будет возвращена, если число отобранных приборов, нуждающихся в настройке, будет больше 6%, т.е. m₁ = 500 × 6/100 = 30. Далее: p = 0,05: q = 0,95; np = 25; 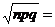4,87. За успех считаем, если прибор требует дополнительной настройки.

Применим интегральную теорему Муавра–Лапласа.

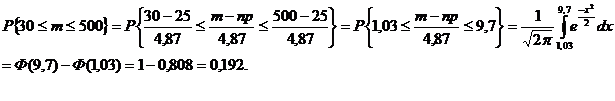
Задача 2. Определить, сколько надо отобрать изделий, чтобы с вероятностью 0,95 можно было утверждать, что относительная частота бракованных изделий будет отличаться от вероятности их появления не более чем на 0,01.

Решение.Для решения задачи выберем в качестве математической модели схему Бернулли и воспользуемся формулой (4). Надо найти такое n, чтобы выполнялось равенство (4), если e = 0,01, b = 0,95, вероятность р неизвестна.

Ф(х_b) = (1 + 0,95) / 2 = 0,975. По таблице приложения найдем, что х_b = 1,96. Тогда по формуле (4) найдем n = ¼ × 1,96²/0,01² = 9600.

Равномерное распределение

Определение 5. Непрерывная случайная величина Х, принимающая значение на отрезке [a,b], имеет равномерное распределение, если плотность распределения имеет вид

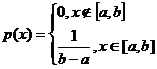. (1)

Нетрудно убедиться, что ,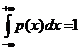

.

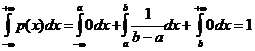Если случайная величина равномерно распределена, то вероятность того, что она примет значение из заданного интервала [x; x+∆] не зависит от положения интервала на числовой прямой и пропорциональна длине этого интервала

^.

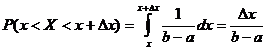Покажем, что функция распределения Х имеет вид

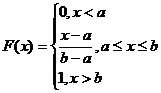. (2)

Пусть хÎ (–¥,a), тогда F(x) = .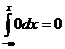

Пусть хÎ [a,b], тогда F(x) = .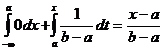

Пусть х Î (b,+¥], тогда F(x) = 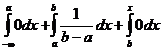= 0 + .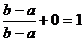

Найдем медиану x_0,5. Имеем F(x_0,5) = 0,5, следовательно

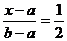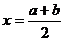, . Итак, медиана равномерного распределения совпадает с серединой отрезка [a, b]. На рис.1 приведен график плотности р(х) и функции распределения F(x)

для равномерного распределения.

Рис. 1

Нормальное распределение

Определение 7. Непрерывная случайная величина имеет нормальное распределение, с двумя параметрами a, s, если

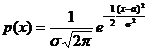, s>0. (5)

Тот факт, что случайная величина имеет нормальное распределение, будем кратко записывать в виде Х ~ N(a;s).

Покажем, что p(x) – плотность

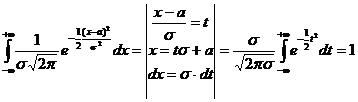(показано в лекции 6).

График плотности нормального распределения (рис. 3) называют нормальной кривой (кривой Гаусса).

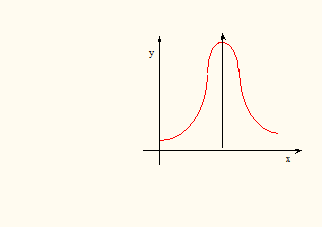
Рис.3

Плотность распределения симметрична относительно прямой х = a. Если х ® ¥, то р(х) ® 0. При уменьшении s график «стягивается» к оси симметрии х = a.

Нормальное распределение играет особую роль в теории вероятностей и ее приложениях. Это связано с тем, что в соответствии с центральной предельной теоремой теории вероятностей при выполнении определенных условий сумма большого числа случайных величин имеет «примерно» нормальное распределение.

Так как 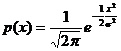– плотность нормального закона распределения с параметрами а = 0 и s =1, то функция 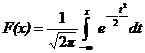= Ф(х), с помощью которой вычисляется вероятность 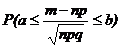, является функцией распределения нормального распределения с параметрами а = 0 и s =1.

Функцию распределения случайной величины Х с произвольными параметрами а, s можно выразить через Ф(х) – функцию распределения нормальной случайной величины с параметрами а = 0 и s =1.

Пусть Х ~ N(a;s), тогда

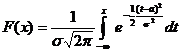. (6)

Сделаем замену переменных под знаком интеграла 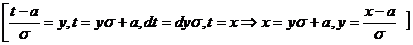, получим

=

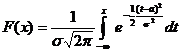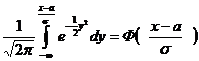
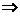
F(x) = 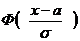. (7)

В практических приложениях теории вероятностей часто требуется найти вероятность того, что случайная величина примет значение из заданного отрезка 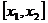. В соответствии с формулой (7) эту вероятность можно найти по табличным значениям функции Лапласа

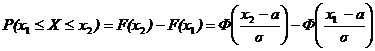. (8)

Найдем медиану нормальной случайной величины Х ~ N(a;s). Так как плотность распределения р(х) симметрична относительно оси х = а, то

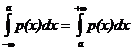
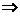
р(х < a) = p(x > a) = 0,5.

Следовательно, медиана нормальной случайной величины совпадает с параметром а:

Х_0,5 = а.

Задача 1. Поезда в метро идут с интервалом в 2 мин. Пассажир выходит на платформу в некоторый момент времени. Время Х, в течение которого ему придется ждать поезд, представляет собой случайную величину, распределенную с равномерной плотностью на участке (0, 2) мин. Найти вероятность того, что пассажиру придется ждать ближайший поезд не более 0,5 мин.

Решение. Очевидно, что p(x) = 1/2. Тогда, Р_0,5 = Р(1,5<X<2) = 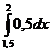= 0,25

Задача 2. Волжский автомобильный завод запускает в производство новый двигатель. Предполагается, что средняя длина пробега автомобиля с новым двигателем – 160 тыс. км, со стандартным отклонением – σ = 30 тыс.км. Чему равна вероятность, что до первого ремонта число км. пробега автомобиля будет находиться в пределах от 100 тыс. км. до 180 тыс. км.

Решение. Р(100000< X < 180000) = 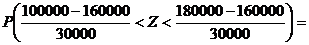Ф(2/3)–Ф(–2) = 0,2454 + 0,4772 = 0,7226.

Свойства дисперсии

1.Дисперсия постоянной C равна 0,DC = 0, С = const.

Доказательство. DC = M(С – MC)² = М(С – С) = 0.

2. D(CX) = С²DX.

Доказательство. D(CX) = M(CX)² – M²(CX) = C²MX² – C²(MX)² = C²(MX² – M²X) = С²DX.

3. Если X и Y – независимые случайные величины, то

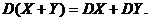
Доказательство.

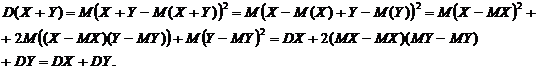
4. Если Х₁, Х₂, … не зависимы, то .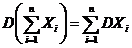

Это свойство можно доказать методом индукции, используя свойство 3.

5. .

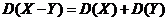Доказательство. D(X – Y) = DX + D(–Y) = DX + (–1)²D(Y) = DX + D(Y).

6.

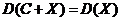
Доказательство. D(C+X) = M(X+C–M(X+C))² = M(X+C–MX–MC)² = M(X+C–MX–C)² = M(X–MX)² = DX.

Пусть 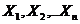– независимые случайные величины, причем , .

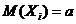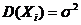Составим новую случайную величину 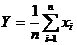, найдем математическое ожидание и дисперсию Y.

; .

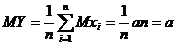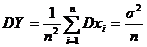
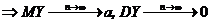То есть при n®¥ математическое ожидание среднего арифметического n независимых одинаково распределенных случайных величин остается неизменным, равным математическому ожиданию а, в то время как дисперсия стремится к нулю.

Это свойство статистической устойчивости среднего арифметического лежит в основе закона больших чисел.

Нормальное распределение

Пусть X имеет нормальное распределение. Раннее, в лекции 11 (пример 2) было показано, что если

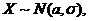
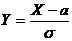, то Y ~ N(0,1).

Отсюда 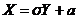, и тогда 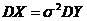, поэтому найдем сначала DY.

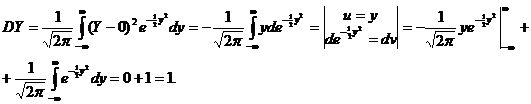
Следовательно

DX = D(sY+a) = s²DY = s², s_x = s. (2)

Распределение Пуассона

Как известно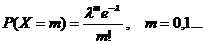

Ранее мы показали, что 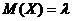, воспользуемся формулой .

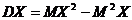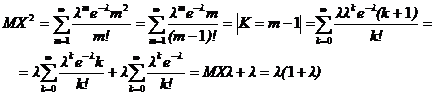
Следовательно,

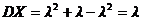(4)

Равномерное распределение

Известно, что .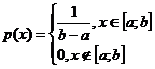

Ранее мы показали, что 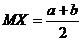, воспользуемся формулой .

,

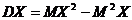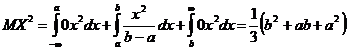тогда

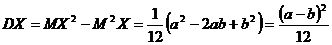. (5)

Доказательство.

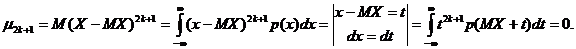
Последний интеграл в цепочке равенств равен 0, так как из условия задачи следует, что p(MX+t) – четная функция относительно t (p(MX+t) = p(MX-t)), а t^2k+1 – нечетная функция.

Так как плотности нормального и равномерного законов распределений симметричны относительно х = МХ, то все центральные моменты нечетного порядка равны 0.

Теорема 2.Если X~N(a,s), то .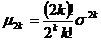

Чем больше моментов случайной величины известно, тем более детальное представление о законе распределения мы имеем. В теории вероятностей и математической статистике наиболее часто используются две числовые характеристики, основанные на центральных моментах 3-го и 4-го порядков. Это коэффициент асимметрии и эксцесс случайной величины.

Определение 3. Коэффициентом асимметрии случайной величины Х называется число b = .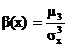

Коэффициент асимметрии является центральным и начальным моментом нормированной случайной величины Y, где 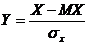. Справедливость этого утверждения следует из следующих соотношений:

.

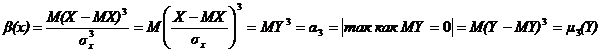Асимметрия случайной величины Х равна асимметрии случайной величины Y = αХ + β

c точностью до знака α, 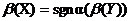. Это следует из того, что нормирование случайных величин aХ+ b и Х приводит к одной и той же случайной величине Y с точностью до знака

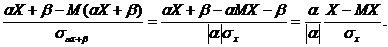
Если распределение вероятностей несимметрично, причем «длинная часть» графика расположена справа от центра группирования, то β(х) > 0; если же «длинная часть» графика расположена слева, то β(х) < 0. Для нормального и равномерного распределений β = 0.

В качестве характеристики большей или меньшей степени «сглаженности» кривой плотности или многоугольника распределения по сравнению с нормальной плотностью используется понятие эксцесса.

Определение 4. Эксцессом случайной величины Х называется величина

g = .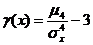

Эксцесс случайной величины Х равен разности начального и центрального моментов 4-го порядка нормированной случайной величины 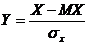и числа3, т.е. 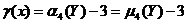. Покажем это:

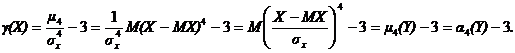
Эксцесс случайной величины Х равен эксцессу случайной величины

Y = αХ + β.

Найдем эксцесс нормальной случайной величины Х.

Если Х~N(a,s), то 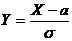~ (0,1).

Тогда

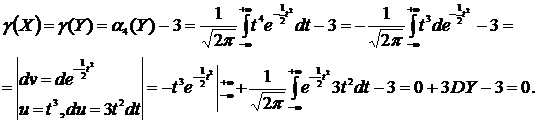
Таким образом, эксцесс нормально распределенной случайной величины равен 0. Если плотность распределения одномодальна и более «островершинна», чем плотность нормального распределения с той же дисперсией, то g(Х) > 0, если при тех же условиях менее «островершинна», то g(Х) < 0.

Закон больших чисел

Закон больших чисел устанавливает условия сходимости среднего арифметического случайных величин к среднему арифметическому математических ожиданий.

Определение 1. Последовательность случайных величин 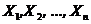называется сходящейся по вероятности p к числу b, если

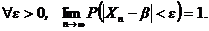
Сходимость по вероятности коротко обозначают так: .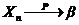

Теорема 2. (Закон больших чисел в форме Чебышева) Пусть 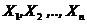– последовательность независимых случайных величин, дисперсии которых равномерно ограничены сверху, т.е. 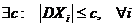; математические ожидания конечны, тогда

.

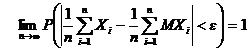Доказательство. Так как DX_i £ c, i = 1, 2, …, n, то 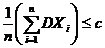. Используя формулу (5) (следствие 2), имеем

.

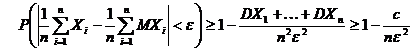Так как вероятность любого события не превышает единицы, получим двойное неравенство

.

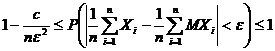Перейдем в этом неравенстве к пределу при 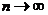и получим

.

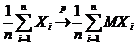Интервальная оценка

Если получена точечная оценка неизвестного параметра по выборке, то говорить о полученной оценке как об истинном параметре довольно рискованно. В некоторых случаях, целесообразнее, получив разброс оценки параметра, говорить об интервальной оценке истинного значения параметра. В качестве иллюстрации сказанного рассмотрим построение доверительного интервала для математического ожидания нормального распределения.

Мы показали, что 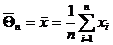– наилучшая оценка (абсолютно корректная) для математического ожидания МХ = Q, поэтому является абсолютно корректной оценкой также и для параметра a = нормального распределения

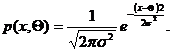
по выборке объема n. Предположим, что задана выборка Х_i, i= 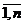. Дисперсия генеральной совокупности известна и равна s². Как далеко может находиться случайная величина от неизвестного математического ожидания Q, оценкой которого она является? Чтобы ответить на этот вопрос, рассмотрим случайную величину 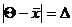, представляющую отклонение от Q. Отклонение D может изменяться от 0 до +¥, но нас интересует, прежде всего, вероятность того, что отклонение D не превысит предельной ошибки e допустимого уровня

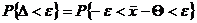. (8)

В формуле (8) только величина является случайной, поэтому вероятность Р зависит только от распределения .

Очевидно, что события A = {–e<Q– <e} и B = {–e+ <Q<e+ } эквивалентны, так как если произойдет событие А, то произойдет и событие В и наоборот. Поэтому

Р{–e+Q< <e+Q} = Р{–e+ <Q<e+ }. (9)

Таким образом, если 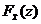– функция распределения непрерывной, случайной величины , то

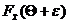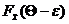Р{–e+Q< <e+Q}= – (10)

Определим функцию распределения 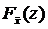случайной величины , где х_i Î N(q,s²). Известно, что линейная функция от нормальных случайных величин является нормальной. Поэтому – нормальная, а нормальная случайная величина задается двумя параметрами – математическим ожиданием и дисперсией, но

.

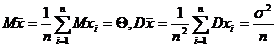Таким образом, плотность распределения имеет вид

.

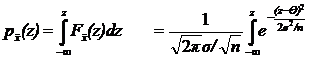Поэтому Р{-e+Q< <e+Q}= .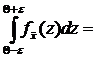

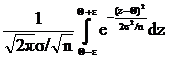В полученном интеграле произведем замену переменных u= 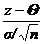, получим

Р{-e+Q< <e+Q}=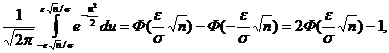

где Ф(z) – функция распределения нормированной нормальной случайной величины.

Таким образом,

Р{-e+ <Q<e+ }= 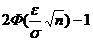. (11)

Если обозначить -e+ = Q₁, e+ = Q₂, то получим интервал (Q_1, Q₂), который накрывает с вероятностью, равной 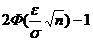, неизвестную величину Q и эта вероятность не зависит от Q, т.е., она одна и та же для любых значений Q. Чтобы найти сам интервал, надо по выборке вычислить и задать e.

Можно по заданной вероятности Р найти концы интервала. Для этого надо воспользоваться формулой 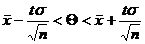, где t – значение аргумента функции Лапласа, при котором Ф(t ) = 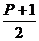, e = .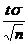

БИБЛИОГРАФИЧЕСКИЕ ССЫЛКИ

1. Колемаев В.А., Староверов О.В., Турундаевский В.Б. Теория вероятностей и мате-

матическая статистика. М.: Высшая Школа, 1991.

2. Елисеева И.И., Князевский В.С., Ниворожкина Л.И., Морозова З.А. Теория статистики с основами теории вероятностей. М.: Юнити, 2001.

3. Секей Г. Парадоксы в теории вероятностей и математической статистике. М.: Мир, 1990.

4. Кремер Н.Ш. Теория вероятностей и математическая статистика. М.: Юнити, 2001

5. Смирнов Н.В. Дунин-Барковский И.В. Курс теории вероятностей и математической статистики для технических приложений. М.: Наука,1969.

6. Статистические методы построения эмпирических формул. М.: Высшая Школа, 1988.

ОГЛАВЛЕНИЕ

ЛЕКЦИЯ 1. ТЕОРИИ ВЕРОЯТНОСТЕЙ. ИСТОРИЯ ВОЗНИКНОВЕНИЯ. КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ.. 3

ЛЕКЦИЯ 2. ТЕОРЕМЫ СЛОЖЕНИЯ И УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ. СТАТИСТИЧЕСКОЕ, ГЕОМЕТРИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ.. 8

ЛЕКЦИЯ 3. АКСИОМАТИЧЕСКОЕ ПОСТРОЕНИЕ ТЕОРИИ ВЕРОЯТНОСТЕЙ. АКСИОМАТИКА КОЛМОГОРОВА.. 14

ЛЕКЦИЯ 4. СЛУЧАЙНАЯ ВЕЛИЧИНА. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ.. 17

ЛЕКЦИЯ 5. РАСПРЕДЕЛЕНИЯ ДИСКРЕТНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН.. 21

ЛЕКЦИЯ 6. ИНТЕГРАЛЬНАЯ ТЕОРЕМА МУАВРА–ЛАПЛАСА, ТЕОРЕМА БЕРНУЛЛИ.. 26

ЛЕКЦИЯ 7. НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ... 29

ЛЕКЦИЯ 8. ПОНЯТИЕ МНОГОМЕРНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ... 35

ЛЕКЦИЯ 9. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ МНОГОМЕРНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ... 39

ЛЕКЦИЯ 10. СВОЙСТВА ПЛОТНОСТИ ВЕРОЯТНОСТЕЙ ДВУМЕРНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ 43

ЛЕКЦИЯ 11. ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН.. 48

ЛЕКЦИЯ 12. ТЕОРЕМА О ПЛОТНОСТИ СУММЫ ДВУХ СЛУЧАЙНЫХ ВЕЛИЧИН.. 52

ЛЕКЦИЯ 13. РАСПРЕДЕЛЕНИЯ СТЬЮДЕНТА, ФИШЕРА .ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫ