Глава 1. Определение и история возникновения понятия размещения

ВВЕДЕНИЕ

Темой данной курсовой работы являются размещения и их свойства. В данной работе будет рассматриваться комбинаторика как раздел математики в целом, в том числе история ее возникновения, и ее элементы в частности, а конкретно число размещений из n элементов по k.

Актуальность исследования комбинаторики в целом и в том числе этой ее области заключается в широком спектре ее использования, как в разных научных отраслях, так и в обиходе. Комбинаторика является одним из наиболее популяризованных разделов математики, поскольку, кроме научного интереса у ученых, она вызывает и обычный живой интерес у людей, не вовлеченных в научную сферу.

В ходе данной работы я ставлю перед собой задачи:

1. Проанализировать и изучить различную литературу по темам «Дискретная математика» и «Комбинаторика»;

2. Изучить исторические сведения, касающиеся возникновения комбинаторики как раздела математики;

3. Проанализировать и изучить теоретический материал по теме «Размещения»;

4. Разобрать на практических примерах особенности чисел размещений с повторениями и без повторений.

Целью данной курсовой работы является исследование путей развития комбинаторики как раздела математической науки, а так же анализ практических задач, решение которых опирается на правила комбинаторики и различные относящиеся к ней вычислительные формулы.

Объектом исследования является история становления комбинаторики как науки и ее теоретические и практические основы.

Предметом исследование являются элементы комбинаторики, а в особенности число размещений.

Данная курсовая работа состоит из введения, двух глав, заключения и списка литературы.

Глава 1. Определение и история возникновения понятия размещения

Число подмножеств конечного множества

Рассмотрим его на примере данного множества A, состоящего из трех элементов: 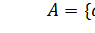. Перечислим все подмножества множества А:

;

;

;

;

;

;

;

.

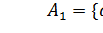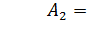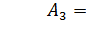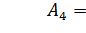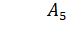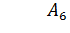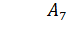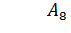Обозначим множество всех подмножеств множества А. Тогда получаем,что число элементов множества равно 8, при условии, что число элементов множества А равно 3.

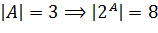
Пусть множество .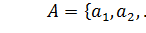

Каждому подмножеству множества А поставим в соответствие n-элементный набор, состоящий из 0 и 1:

;

;

;

;

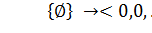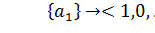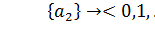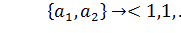И т.д.

.

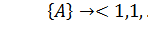Тогда число всех подмножеств равно числу всех таких наборов, а оно, в свою очередь, вычисляется по формуле:

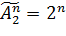
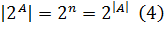
Выводы к главе 1

Комбинаторика формировалась как наука в течение довольно долгого периода, и она все еще развивается. Она широко используется как в обиходе (например, в играх), так и в других науках, и тесно связана с различными областями математики (алгеброй, геометрией, теорией вероятностей и др.). Иногда в широком понимании под комбинаторикой подразумевают более обширную область дискретной математики, включающую, в том числе, и теорию графов. Однако наиболее знакомой для нас является вероятностная и перечислительная комбинаторика. Первая изучает вопрос вероятности обладания некоторого множества конкретным свойством, вторая же рассматривает задачи о перечислении или исчислении количества различных конфигураций (перестановок, размещений, сочетаний). Данная работа сфокусирована на размещениях и исследовании их теоретических и практических особенностей.

По окончанию первой главы мы можем заключить, что комбинаторика имеет интересную историю собственного становления как науки. А ее различные разделы имеют широкий спектр применения в различных сферах знаний.

Глава 2. Примеры решения задач по комбинаторике

Выводы к главе 2

Таким образом, существует много типов задач, сводящихся к нахождению числа размещений с повторениями и без повторений. В том числе могут встречаться задачи, где комбинируются числа размещений, сочетаний и перестановки. Необходимый уровень владения теоретическим материалом и практическими навыками в области решения комбинаторных задач существенно упрощает процесс поиска решений, так как зачастую существует очень много способов и подходов к решению одного и того же задания. Умение видеть простейший из них позволяет быстрее и эффективнее найти требуемое решение. Из чего можно сделать вывод, что должным образом изученная и рассмотренная теоретическая часть должна быть подкреплена соответствующими практическими навыками, что позволит быстрее и проще продвигаться в изучении и исследовании различных областей знаний, в том числе и математичеких.

ЗАКЛЮЧЕНИЕ

В ходе исследования темы «Размещения» были изучены и проанализированы найденные исторические сведения и теоретический материал, благодаря чему было выявлено, что комбинаторика формируется и развивается в течение уже очень долгого времени. Ее история насчитывает много веков. Хотя в качестве раздела науки она начала развиваться сравнительно недавно. Значительный вклад в ее развитие внесли известные ученые-математики, такие как Паскаль, Лейбниц, Бернулли, Эйлер и многие другие задолго до них, к примеру, в Древней Греции и Индии.

В ходе исследования теоретического материала и практических задач темы «Размещения» было выявлено, что комбинаторика имеет связи с различными областями математики, такими как алгебра, геометрия, теория вероятностей, а так же имеет широкий спектр применения в разных областях знаний (генетике, информатике, статистической физике).

Различные задачи на размещения в комбинаторике опираются как на абсолютно абстрактные ситуации, так и на вполне способные на существованию, что говорит о практической пользе науки.

К тому же, как уже говорилось ранее, комбинаторика достаточно популяризованная наука на данный момент. Так, к примеру, в книге Н. Я. Виленкина «Популярная комбинаторика» (1975 г.) [6] научно-популярным, доступным и понятным языком рассказывается история возникновения комбинаторики, ее основы, а также в книге представлены комбинаторные задачи. В целом ее можно считать очень понятным учебником по комбинаторике с подробной и интересной исторической справкой. На примере этой книги можно показать, что популяризация комбинаторики проходит достаточно успешно. Кроме того это наука действительно интересна не только для ученых, но и для людей не вовлеченных в науку тоже.

Таким образом, в ходе проведенного исследования и реализации всех поставленных мной целей этой работы было выявлено, что комбинаторика тесно связана со многими разделами математики, широко применяется в различных сферах знаний. А также она может применяться и для решения привычных нам задач, связанных с окружающим нас бытом.

Список литературы

1. http://hijos.ru/izuchenie-matematiki/algebra-10-klass/18-kombinatorika-razmeshheniya-perestanovki-sochetaniya/

2. Айгнер М. Комбинаторная теория. М.: Мир, 1982.

3. Андерсон, Джеймс. Дискретная математика и комбинаторика = Discrete Mathematics with Combinatorics. — М.: «Вильямс», 2006. — С. 960. — ISBN 0-13-086998-8.

4. Белешко Дмитрий Дискретная математика: алгоритмы.– СПб: Изд-во СПбНИУ ИТМО, 2004.

5. Бородин А.И., Бугай А.С. Биографический словарь деятелей в области математики. Киев: Ряданська школа, 1979.

6. Виленкин Н. Я. Популярная комбинаторика . — М.: Наука, 1975.

7. Грэхем Р., Кнут Д., Паташник О. Конкретная математика. М.: Мир, 1998.

8. Ерош И. Л. Дискретная математика. Комбинаторика — СПб.: СПбГУАП, 2001. — 37 c.

9. Ерусалимский Я. М. Дискретная математика: теория, задачи, приложения. 10-е изд., перераб. и доп.– М.: Вузовская книга, 2009, 288 с.

10. История математики с дрвнейших времён до начала XIX столетия / Под ред. А.Н. Колмогорова, А.П. Юшкевича. М: Наука, 1970-1972. T.1-3.

11. Клейн Ф. Лекции о развитии математики в XIX столетии. М.: Наука, 1989.

12. Липский В. Комбинаторика для программиста. — М.: Мир, 1988. — 213 с.

13. Райгородский А. М. Линейно-алгебраические и вероятностные методы в комбинаторике . — Летняя школа «Современная математика». — Дубна, 2006.

14. Раизер Г. Дж. Комбинаторная математика. — пер. с англ. — М., 1966.

15. Рейнгольд Э., Нивергельт Ю., Део Н. Комбинаторные алгоритмы. Теория и практика. — М.: Мир, 1980. — 476 с.

16. Риордан Дж. Введение в комбинаторный анализ. — пер. с англ. — М., 1963.

17. Романовский И.В. Дискретный анализ. — 3-е изд. — СПб: Невский Диалект; БХВ Петербург, 2003.

18. Рыбников К.А. Введение в комбинаторный анализ.– М.: Изд-во МГУ, 1985

19. Рыбников К.А. История математики. М.: МГУ, 1994.

20. Сачк пов В.Н Введение в Комбинаторные методы дискретной математики.– М.: Наука, 1982

21. Стенли Р. Перечислительная комбинаторика = Enumerative Combinatorics. — М.: «Мир», 1990. — С. 440. — ISBN 5-03-001348-2.

22. Стенли Р. Перечислительная комбинаторика. Деревья, производящие функции и симметрические функции = Enumerative Combinatorics. Volume 2. — М.: «Мир», 2009. — С. 767. — ISBN 978-5-03-003476-8.

23. Степанов В. Элементы комбинаторики.– СПб., 2004.

24. Холл М. Комбинаторика.– М.: Мир, 1970

25. Яблонский С.В. Введениев дискретную математику: Учеб. Пособие для вузов.- 2-е изд., перераб. И доп.- М.: Наука, 1986. Гл. ред. Физ.-мат. аЛит.- 384 с..

ВВЕДЕНИЕ

Темой данной курсовой работы являются размещения и их свойства. В данной работе будет рассматриваться комбинаторика как раздел математики в целом, в том числе история ее возникновения, и ее элементы в частности, а конкретно число размещений из n элементов по k.

Актуальность исследования комбинаторики в целом и в том числе этой ее области заключается в широком спектре ее использования, как в разных научных отраслях, так и в обиходе. Комбинаторика является одним из наиболее популяризованных разделов математики, поскольку, кроме научного интереса у ученых, она вызывает и обычный живой интерес у людей, не вовлеченных в научную сферу.

В ходе данной работы я ставлю перед собой задачи:

1. Проанализировать и изучить различную литературу по темам «Дискретная математика» и «Комбинаторика»;

2. Изучить исторические сведения, касающиеся возникновения комбинаторики как раздела математики;

3. Проанализировать и изучить теоретический материал по теме «Размещения»;

4. Разобрать на практических примерах особенности чисел размещений с повторениями и без повторений.

Целью данной курсовой работы является исследование путей развития комбинаторики как раздела математической науки, а так же анализ практических задач, решение которых опирается на правила комбинаторики и различные относящиеся к ней вычислительные формулы.

Объектом исследования является история становления комбинаторики как науки и ее теоретические и практические основы.

Предметом исследование являются элементы комбинаторики, а в особенности число размещений.

Данная курсовая работа состоит из введения, двух глав, заключения и списка литературы.

Глава 1. Определение и история возникновения понятия размещения