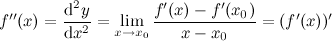Производная показательно-степенной функции

Рационально использовать логарифмическое дифференцирование и при нахождении производной показательно-степенной (или степенно-показательной) функции или "функции в степени функция", то есть в случае, когда заданная функция имеет вид 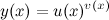. Логарифмируем левую и правую часть:

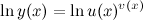
далее по свойствам логарифма

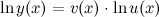
Тогда

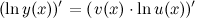
Производную в левой части равенства находим как производную сложной функции, а в правой - как производную произведения:

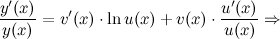
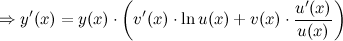
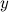Если независимая переменная и функция связаны уравнением вида 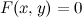, которое не разрешено относительно 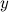, то функция 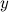называется неявной функцией переменной .

Всякую явно заданную функцию можно записать в неявном виде 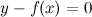. Обратно сделать не всегда возможно.

Несмотря на то, что уравнение 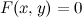не разрешимо относительно 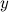, оказывается возможным найти производную от 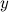по . В этом случае необходимо продифференцировать обе части заданного уравнения, рассматривая функцию 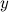как функцию от , а затем из полученного уравнения найти производную .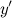

Билет №30. Дифференциал ф-и, его геометрический смысл. Основные формулы и правила для дифференциалов.

Пусть функция дифференцируема в точке , то есть приращение этой функции можно представить в виде суммы двух слагаемых: линейного относительно и нелинейного членов:

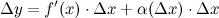
где 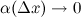при .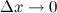

Дифференциалом функции называется линейная относительно часть приращения функции. Она обозначается как 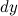или 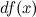. Таким образом:

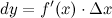
Замечание

Дифференциал функции составляет основную часть ее приращения.

Замечание

Наряду с понятием дифференциала функции вводится понятие дифференциала аргумента. По определению дифференциал аргумента есть приращение аргумента:

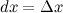
Замечание

Формулу для дифференциала функции можно записать в виде:

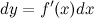
Отсюда получаем, что

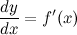
Итак, это означает, что производная может быть представлена как обыкновенная дробь - отношение дифференциалов функции и аргумента.

Геометрический смысл дифференциала

Дифференциал функции в точке 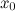равен приращению ординаты касательной, проведенной к графику функции в этой точке, соответствующему приращению аргумента .

Правила вычисления дифференциалов

1. Константу можно выносить за знак дифференциала.

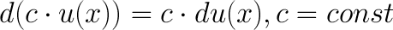
2. Дифференциал суммы/разности.

Дифференциал суммы/разности функций равен суме/разности дифференциалов от каждого из слагаемых.

3. Дифференциал произведения.

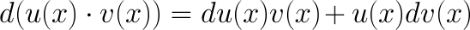
4. Дифференциал частного.

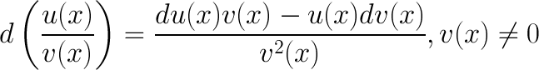
5. Дифференциал константы равен нулю.

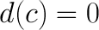
Билет №31. Инвариантность формы дифференциала первого порядка. Приложение дифференциалов к приближенным вычислениям.

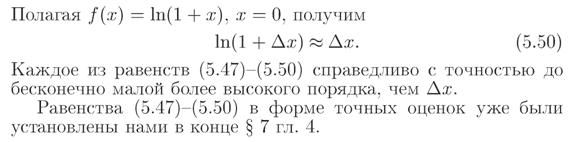
Билет №32. Производные высших порядков. Дифференциалы высших порядков. Нарушение формы дифференциалов высших порядков.

Производные высших порядков

Если функция имеет производную в каждой точке своей области определения, то ее производная 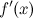есть функция от . Функция 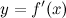, в свою очередь, может иметь производную, которую называют производной второго порядка функции (или второй производной) и обозначают символом 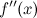. Таким образом