Условие совместности деформаций

Из соотношений Коши вытекает интересное следствие. Вычислим следующие выражения:

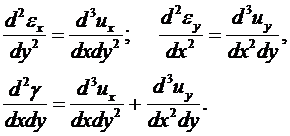
Видно, что:

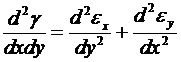. (2.3)

Подставляя сюда g_ху, e_х, e_у по закону Гука получим связь:

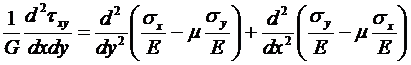. (2.4)

Таким образом, выбирать аппроксимации для напряжений произвольным образом нельзя, так как должно выполняться условие совместности деформаций (2.4). Исключение составляют лишь аппроксимации линейными функциями (как, например, принято в задаче о дамбе), поскольку в этом случае вторые производные от напряжений равны нулю, следовательно, (2.4) выполняется автоматически. Поэтому выгоднее решать задачи, отыскивая не напряжения, а перемещения, через которые напряжения определяются c помощью соотношений Коши и закона Гука.

Решения уравнений теории упругости в напряжениях

Задача о дамбе

Поскольку при оценке прочности обычно необходимо знать лишь напряженное состояние тела, то интерес представляют задачи, в которых удается ограничиться только уравнениями равновесия. Одной из таких является, например, задача о дамбе (рис.3.1). Уравнение линии ВD имеет вид:

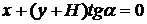. (3.1)

Давление воды увеличивается с глубиной по закону:

p_х = - p₀ ∙(Н-у)/м; р₀=0.1 кг/см². (3.2)

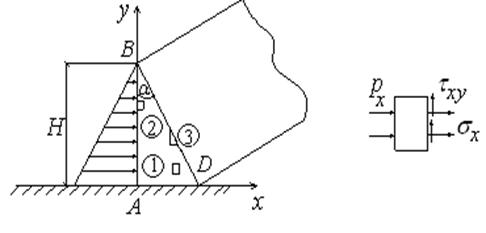
Рис.3.1 Рис.3.2

Считается, что дамба находится в плоском деформированном состоянии. Тогда уравнения равновесия внутреннего элемента имеют вид:

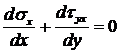, (3.3)

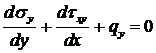. (3.4)

Для простоты в дальнейшем силой веса 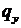дамбы пренебрежем.

Решение ищем в виде:

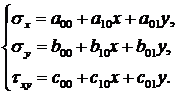(3.5)

Необходимо определить коэффициенты a_ij; b_ij; c_ij .

Из уравнений равновесия внутреннего элемента 1 получаем:

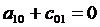- первое уравнение равновесия внутреннего элемента;

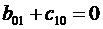- второе уравнение равновесия внутреннего элемента.

Отсюда:

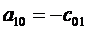, (3.6)

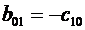. (3.7)

Из уравнений равновесия элемента 2 на левой грани (его координаты: х = 0, у – любое) вытекает (рис 3.3):

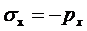, (3.8)

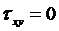. (3.9)

Подставляя сюда (3.3) и (3.5) получаем:

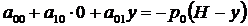, 3.10)

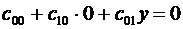. (3.11)

Сначала в качестве координат центра малого элемента 2 примем точку х=0, у=0. Тогда получим из (3.10), (3.11):

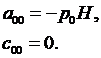
В качестве координат центра малого элемента 3 примем точку х=0, у=Н/2. Подставляя в (3.10) (3.11), получим:

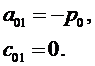
Из (3.6) тогда вытекает, что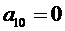

Из уравнения равновесия элемента 3 на наклонной грани (рис.3.1, рис.3.3) следует:

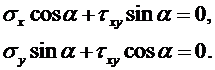
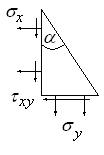
Рис. 3.3

Подставляя сюда (3.5) получаем:

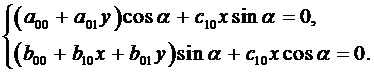(3.12)

Учтем уравнение прямой BD:

.

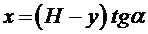Тогда уравнения (3.12) примут вид:

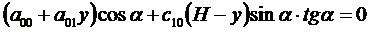. (3.13)

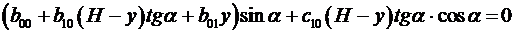.(3.14)

Выберем координаты центра этого элемента в виде:

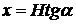, у = 0.

Тогда из уравнения (3.13) вытекает:

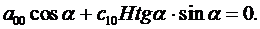(3.15)

Наконец выбирая координаты центра третьего элемента в виде:

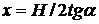, у= H/2,

получаем из уравнения (3.13):

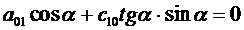. (3.16)

Из (3.15), (3.16) находим, что

с₁₀=р₀ сtg²α, а₀₀= - р₀Н.

Аналогично получаем систему уравнений для отыскания оставшихся неизвестных, подставляя в (3.14) координаты центра элемента, находящегося в вершине дамбы. Тогда решение запишется в виде:

b₀₀=р₀ Н сtg²α, b₁₀= - р₀ сtg³α, b₀₁= - р₀ сtg²α.

Подставляя все коэффициенты в (3.5), получим:

σ_х = р₀ у,

σ_у = (- р₀ сtg³α) х - (р₀ сtg²α) у,

τ_ху = (р₀ сtg²α) х.

Выводы из решения

1. Решение имеет очень простой вид.

2. Это решение не может удовлетворить условия закрепления основания, а именно: условию e_х=0 на линии АВ, поскольку после подстановки вычисленных значений напряжений по закону Гука получим:

.

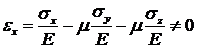Если нас не интересует точность решения в опорной зоне, то решение приемлемо. Однако это противоречие не является существенным, так как условие жесткой заделки является лишь некоторой приближенной заменой реальных условий закрепления. Все недостатки решений такого рода сглаживаются введением коэффициента запаса.

Примечание. Как было отмечено ранее, кроме уравнений равновесия напряжения должны удовлетворять условию совместности деформаций (2.4). В нашем случае оно будет удовлетворяться тождественно, поскольку напряжения представляют собой линейные функции, а в соотношения (2.4) необходимо подставлять вторые производные.