Уравнения равновесия внутреннего малого элемента

Основное отличие теории упругости от сопротивления материалов и строительной механики заключается в следующем. В последних двух дисциплинах используется метод сечений, в котором конструкцию делят на две части. Воздействие одной части на другую заменяют силами и моментами. Эти воздействия находятся из условия, что любая часть конструкции находит в покое. Например, для конструкции, изображенной на рис.1.1, уравнения равновесия отсеченной части имеют вид:

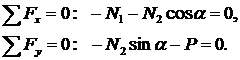
Отсюда:

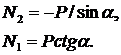
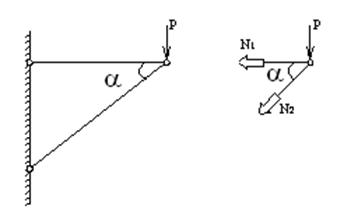
Рис.1.1

В теории упругости из конструкции сечениями выделяется малый элемент (рис.1.2). На него со всех сторон соседние элементы воздействуют давлениями (распределенными по поверхности нагрузками) σ_х, σ_у, σ_z, τ_ху, τ_yz, τ_xz, которые называются напряжениями. Для этого элемента записываются уравнения равновесия, физические соотношения, связывающие напряжения с кинематическими параметрами этого элемента. Совокупность таких уравнений для всех микрочастиц и является объектом изучения теории упругости. Составим уравнения равновесия для малого элемента, изображенного на рис.1.2. Для простоты ограничимся напряжениями σ_х, σ_у, τ_xy , τ_yх .

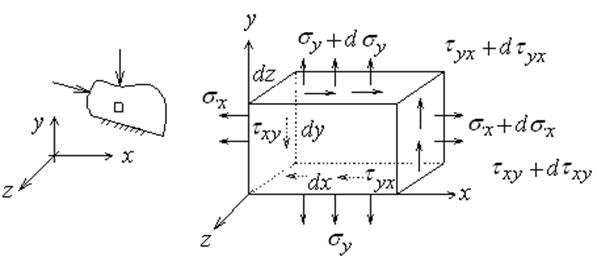
Рис.1.2

Первый индекс в обозначении касательных напряжений показывает площадку, на которую действует напряжение, второй индекс показывает направление.

Правиладля изображения положительного направления напряжений приведены на рис.1.3.

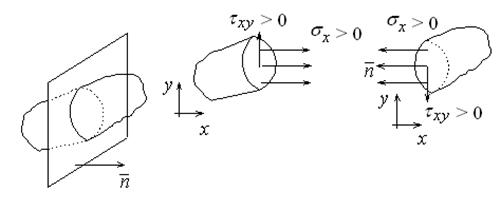
Рис.1.3

Нормаль к грани выбирают так, что она направлена наружу от рассматриваемого элемента. Если направление нормали совпадает с осью х, то положительные σ_х, τ_ху, τ_хz направлены в положительном направлении осей х, у, z, если нет, то напряжения направлены в обратную сторону.

Малые величины, на которые различаются напряжения на правой и левой гранях элемента, обозначим через dσ_х, dσ_у, dτ_xy.

Поскольку малая частица является частью всего тела, то эта частица тоже находится в покое, поэтому можем записать уравнения его равновесия в виде:

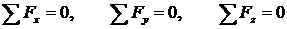. (1.1)

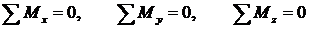. (1.2)

Из первого уравнения вытекает:

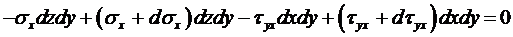. (1.3)

Это уравнение делим на объем 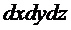. В результате после упрощений получим:

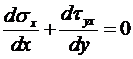. (1.4)

Если имеется воздействие по оси z, то в уравнение добавляется еще одно слагаемое .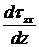

На тело, кроме внешних поверхностных сил могут действовать объемные силы (например, удельный вес). Обозначим эти силы через q_x , q_y, q_z.

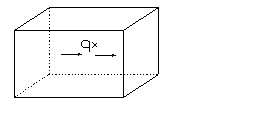
Рис.1.4

Вес параллелепипеда с удельным весом q_x будет:

.

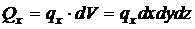Поэтому в уравнение равновесия (1.4) добавится удельный вес q_x.

Таким образом, в общем случае уравнения равновесия примут следующий вид:

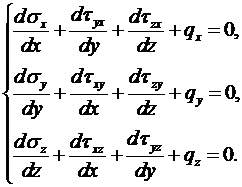(1.5)

Эти соотношения называются дифференциальными уравнениями равновесия внутреннего малого элемента (другими словами, уравнения в приращениях).

Из уравнений равновесия (1.2) вытекает закон парности касательных напряжений,которые приведем без вывода:

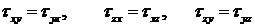.(1.6)

В балках-стенках, плитах, оболочках, используемых, например, в строительстве, как правило, σ_z, τ_yz, τ_xz очень малы. В результате получим следующую более простую систему уравнений:

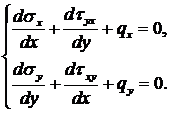(1.7)