Анализ прохождения непериодического сигнала через линейную цепь

Задана линейная цепь (рис. 15), на вход которой поступает непериодический сигнал S₁(t).

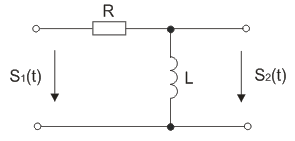
Рис. 16. Линейная RL-цепь

Линейные цепи – это цепи, в которых реакция цепи на сумму входных воздействий равна сумме реакций цепи на каждое отдельное входное воздействие.

Анализ прохождения сигналов через линейные цепи сводится к определению выходного сигнала s₂ (t)- реакция цепи на заданное входное воздействие s₁ (t) [1].

Существуют различные методы анализа прохождения сигналов через линейные цепи, одним из которых является частотный (спектральный) метод, основанный на использовании комплексной частотной характеристики (КЧХ). Спектральная функция выходного сигнала находится как произведение спектральной функции входного сигнала на комплексную частотную характеристику цепи [1]:

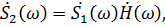(5.1)

где 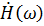– комплексная частотная характеристика цепи.

Обратное преобразование Фурье определяет временное представление выходного сигнала:

(5.2)

Определим КЧХ для RL – цепи. На практике КЧХ определяют как отношение комплексной амплитуды выходного сигнала к комплексной амплитуде входного сигнала:

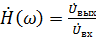, (5.3)

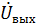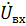, – комплексные амплитуды выходного ( 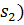и входного ( 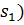сигналов.

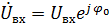. (5.4)

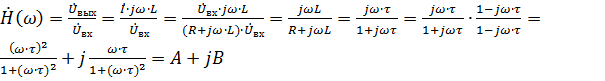(5.5)

где 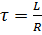– постоянная времени цепи.

Из уравнения (5.5) найдём АЧХ:

Амплитудно-частотная характеристика цепи (АЧХ) – зависимость модуля КЧХ от частоты. Показывает изменение амплитуды гармонического сигнала при прохождении через линейную цепь [1]:

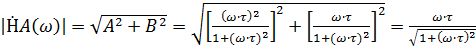(5.6)

Из уравнения (5.5) найдём ФЧХ:

Фазочастотная характеристика (ФЧХ) – зависимость аргумента КЧХ от частоты сигнала. Показывает угол, на который изменится фаза входного сигнала при прохождении через линейную цепь [1]:

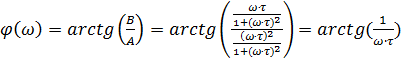(5.7)

Выбор параметров RL-цепи осуществим, используя полосу пропускания цепи.

На граничной частоте АЧХ принимает значение 0.707 от максимального значения. Граничная частота определяется выражением:

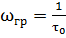(5.8)

Граничная частота равна ширине спектра исходного видеоимпульса:

,

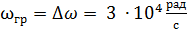тогда 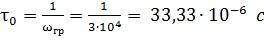(5.9)

Выберем сопротивление резистора R = 100 Ом, тогда индуктивность будет равна:

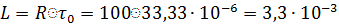Гн

Эти значения соответствуют значениям в номинальном рядуE24.

По формулам (5.6) и (5.7) построим АЧХ и ФЧХ цепи.

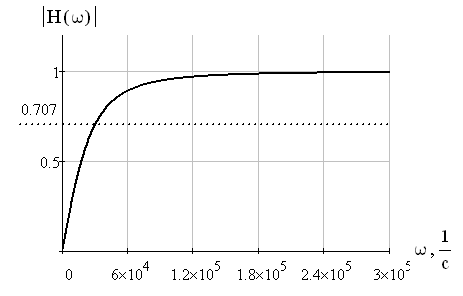
Рис.17 Амплитудно-частотная характеристика RC-цепи

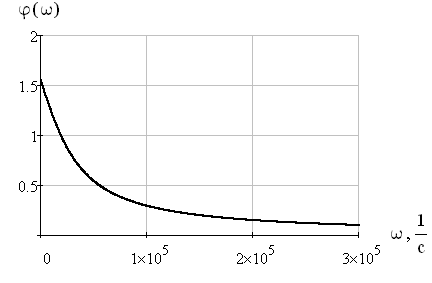
Рис. 18. Фазочастотная характеристика RC-цепи

Таким образом, можно сделать вывод, что при прохождении сигнала через линейную цепь возникают линейные искажения сигнала. На полученных АЧХ и ФЧХ можно увидеть влияние линейной цепи на входной сигнал.

Спектральная плотность выходного сигнала определяется через выражение:

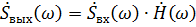(5.10)

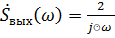ּ(1- 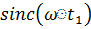)ּ 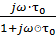(5.11)

Амплитудный спектр сигнала на выходе цепи равен:

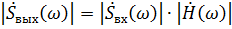(5.12)

Подставим значения из формул и найдем амплитудный спектр сигнала на выходе цепи:

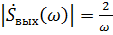ּ(|1- 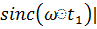)ּ 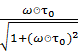(5.13)

По формуле (5.13) построим амплитудный спектр сигнала на выходе линейной цепи.

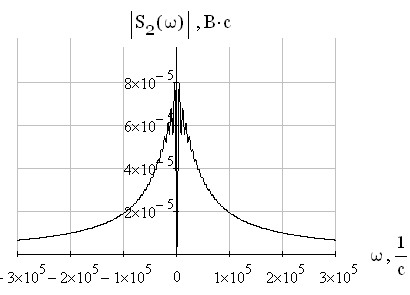
Рис. 19 Спектр выходного сигнала

Временное представление сигнала на выходе цепи можно получить с помощью обратного преобразования Фурье:

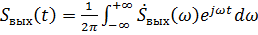(5.14)

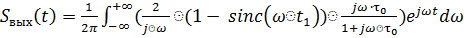(5.15)

Заключение

В процессе выполнения курсовой работы были проведены исследования периодического и непериодического сигнала, были построены графики амплитудного спектра заданных сигналов, исследована автокорреляционная функция непериодического сигнала.

По итогам исследования можно выделить следующие результаты:

Основные особенности амплитудного спектра непериодического сигнала:

1) функция четная

2) спектр положительный

3) спектр двухсторонний

4) спектр сплошной

5) спектр теоретически бесконечен

Основные особенности амплитудного спектра периодического сигнала:

1) спектр двухсторонний при разложении в комплексный ряд Фурье

2) спектр дискретный

3) спектр теоретически бесконечен

4)функция четная

Основные особенности функции автокорреляции:

1. Максимум автокорреляционной функции находится в точке 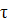=0, B( 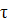) = E

2. Автокорреляционная функция является четной

3. При ,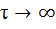

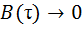
С помощью спектрального метода был произведен анализ заданной линейной цепи, и построены АЧХ и ФЧХ линейной цепи.

В ходе данной работы, на основе теоретических знаний, мы исследовали сигнал в частотной области, используя различные способы нахождения спектров различных типов сигнала.