Основных элементарных функций
1. 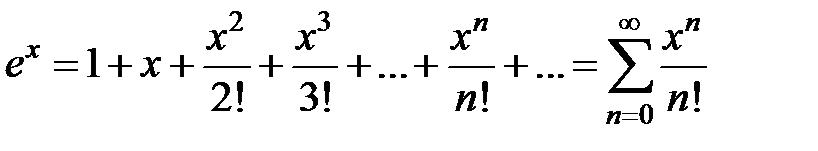 , x Î R.
, x Î R.
2. 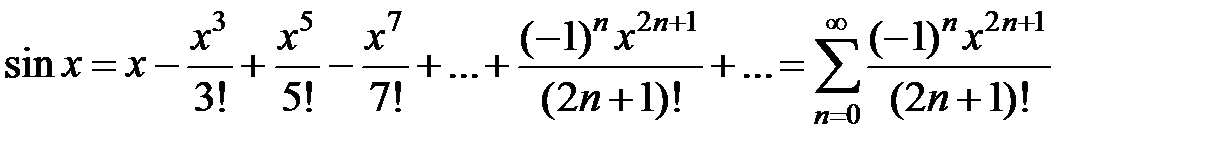 , x Î R
, x Î R
3. 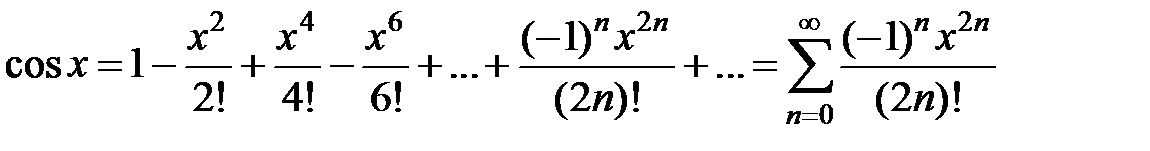 , x Î R
, x Î R
4. 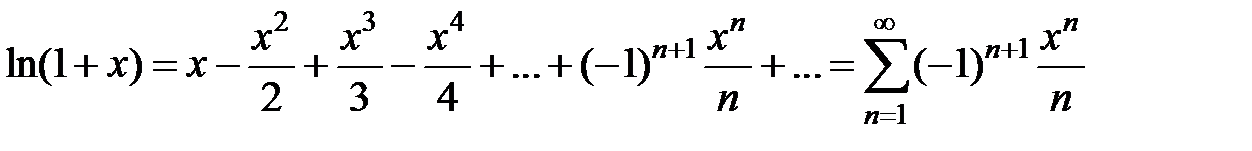 , x Î (−1;1].
, x Î (−1;1].
5. 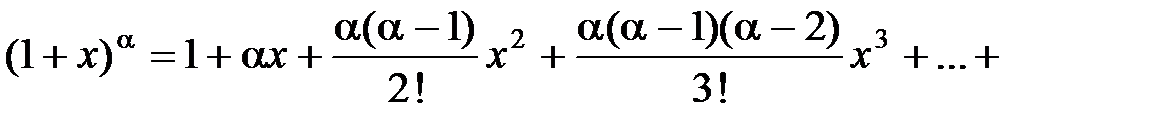
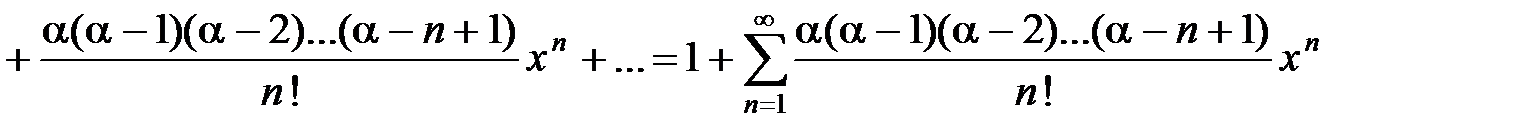 , x Î (−1;1).
, x Î (−1;1).
Пример 9. Разложить функцию f(x) = x3+ 2x – 5 по степеням x – 1.
3Воспользуемся формулой (21), в которой надо взять x0= 1, n = 3 (n – степень многочлена). Вычислим f(1), f /(1), f //(1), f ///(1) и полученные числа подставим в формулу (21).
f(1) = –2,
f /(x) = 3x2+2, f /(1) = 5,
f //(x) = 6x, f //(1) = 6,
f ///(x) = 6.
После подстановки в (21), в которой вместо x – x0надо писать x – 1, окончательно получим x3+ 2x – 5 = –2 + 5(x – 1) +3(x – 1)2+ (x – 1)3.4
Пример 10. Разложить функцию 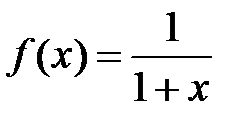 в ряд по степеням x.
в ряд по степеням x.
3По формуле суммы геометрической прогрессии
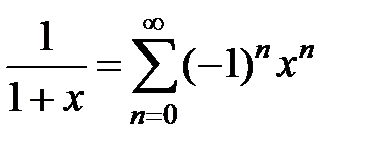 . (36)
. (36)
Ряд сходится при |x| < 1.4
Пример 11. Разложить в ряд по степеням (x + 3) функцию ln(2 – 5x).
3Рассмотрим сначала следующее преобразование данной логарифмической функции:
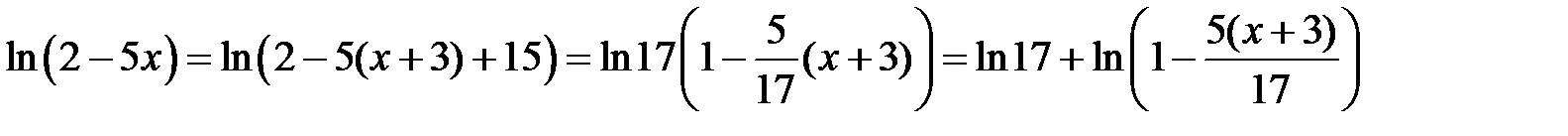 .
.
Воспользуемся разложением (34) для функции ln(1 + t) и положим 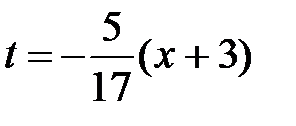 . Так как разложение (34) имеет место при x Î (–1;1], то наше разложение будет иметь место при
. Так как разложение (34) имеет место при x Î (–1;1], то наше разложение будет иметь место при 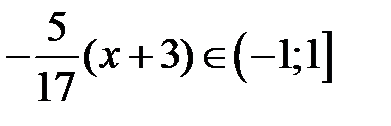 . Таким образом,
. Таким образом, 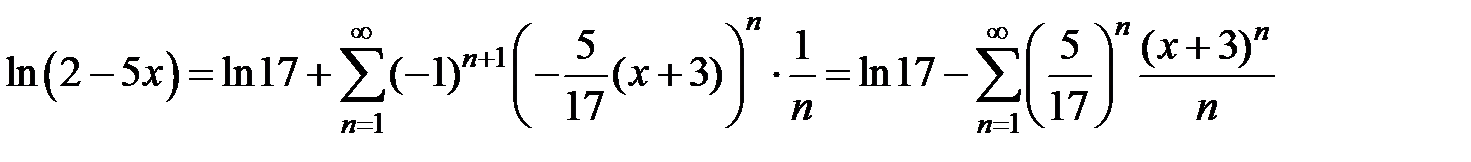 ,
,
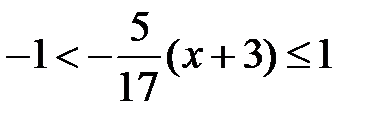 , т.е. ряд сходится при
, т.е. ряд сходится при 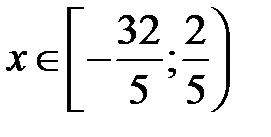 .4
.4
При разложении в ряд Тейлора часто используют почленное дифференцирование и интегрирование степенных рядов.
Пример 12. Разложить в ряд Маклорена функцию f(x) = arctg x.
3Найдем производную f(x), получим
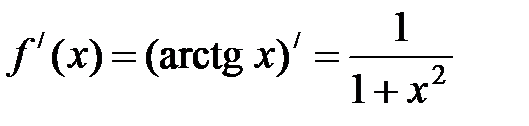 .
.
Заменив в формуле (36) x на x2, получим
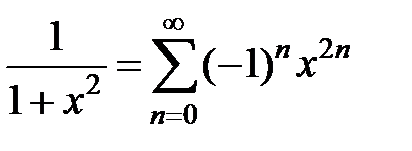 для x Î (–1;1).
для x Î (–1;1).
Интегрируя этот ряд почленно, получаем
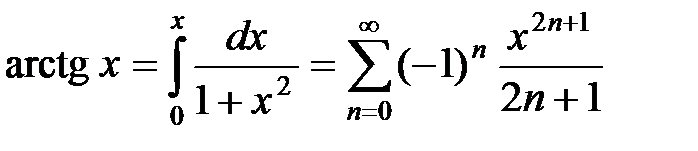 .
.
Так как при почленном интегрировании интервал сходимости сохраняется, то 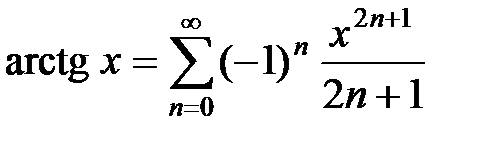 для любого x Î (–1;1].4
для любого x Î (–1;1].4
Используя разложения основных элементарных функций, а также возможность почленного дифференцирования и интегрирования степенных рядов, разложить функции в ряд по степеням 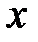 и указать области сходимости полученных рядов.
и указать области сходимости полученных рядов.
227. 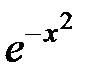 . . | 228. 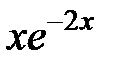 . . |
229. 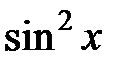 . . | 230. 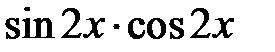 . . |
231. 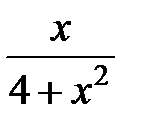 . . | 232. 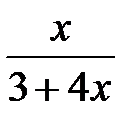 . . |
233. 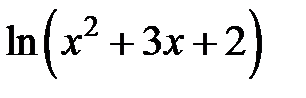 . . | 234. 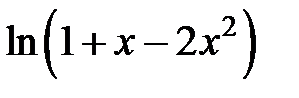 . . |
235. 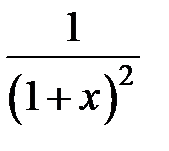 . . | 236. 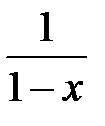 . . |
237. 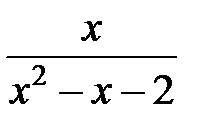 . . | 238. 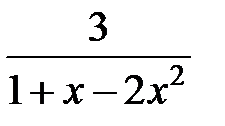 . . |
239. 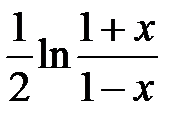 . . | 240. 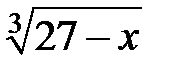 . . |
241. 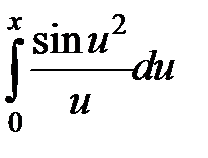 . . | 242. 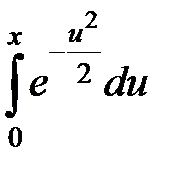 . . |
Разложить функции в ряд по степеням 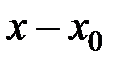 и определить области сходимости полученных рядов.
и определить области сходимости полученных рядов.
243. 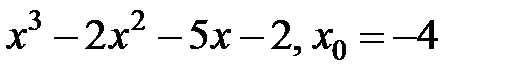 . . | 244. 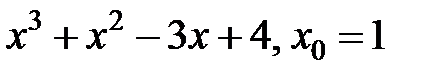 . . |
245. Разложить в ряд Маклорена функцию 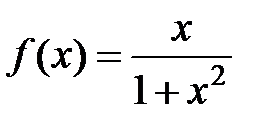 и из полученного ряда почленным дифференцированием получить ряд Маклорена для функции
и из полученного ряда почленным дифференцированием получить ряд Маклорена для функции 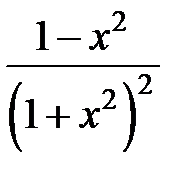 .
.
9.246. Разложить в ряд Маклорена функцию 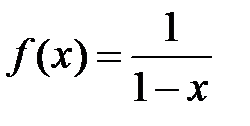 и из полученного ряда почленным дифференцированием получить ряд Маклорена для функции
и из полученного ряда почленным дифференцированием получить ряд Маклорена для функции 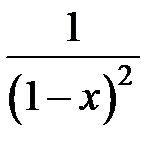 .
.
Задачи повышенной сложности
Разложить функции в ряд по степеням 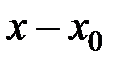 и определить области сходимости полученных рядов.
и определить области сходимости полученных рядов.
247. 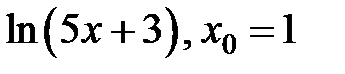 . . | 248. 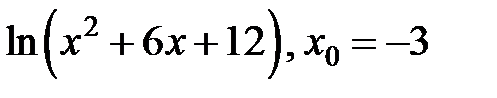 . . |
249. 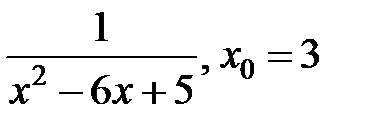 . . | 250. 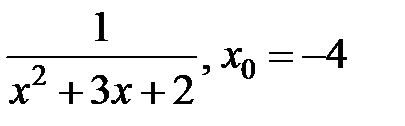 . . |
251. 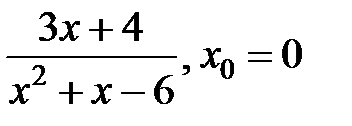 . . | 252. 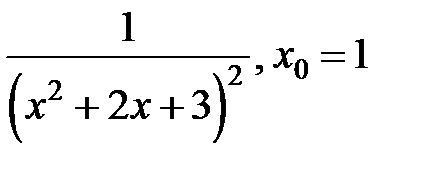 . . |
253. 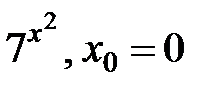 . . | 254. 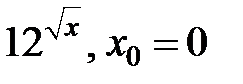 . . |
9.255. 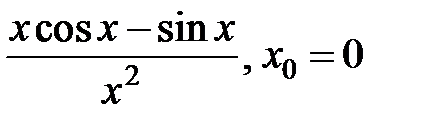 . . | 256. 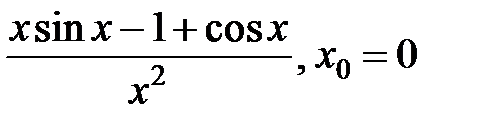 . . |
Используя возможность почленного интегрирования степенных рядов, разложить в ряд Маклорена следующие функции:
257. 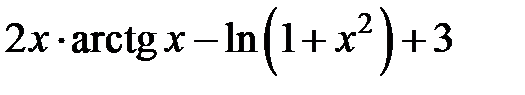 .
.
258. 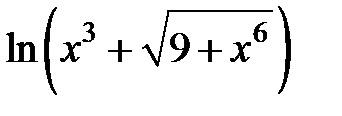 .
.
6.3. Применение степенных рядов
1) Приближенное вычисление значений функции.
Если функция f(x) в интервале (x0– R; x0+ R) разлагается в степенной ряд 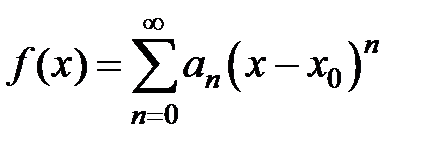 , то в качестве приближенного значения функции f(x) в точке x Î (x0– R; x0+ R) можно взять частичную сумму этого ряда:
, то в качестве приближенного значения функции f(x) в точке x Î (x0– R; x0+ R) можно взять частичную сумму этого ряда: 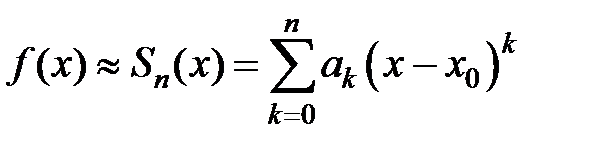 . Точность этого равенства увеличивается с ростом n. Абсолютная погрешность этого приближенного равенства равна модулю остатка ряда, т.е.
. Точность этого равенства увеличивается с ростом n. Абсолютная погрешность этого приближенного равенства равна модулю остатка ряда, т.е.
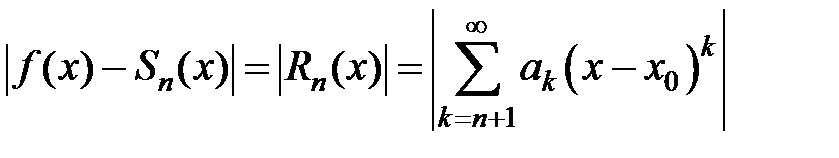 .
.
Оценивать остаток ряда можно различными способами. Можно использовать представление остаточного члена формулы Тейлора в форме Лагранжа, Коши или интегральной (см. гл. 4 §3). Можно, кроме того, строить для ряда числовую мажоранту, сумму которой несложно вычислить. В отдельных случаях можно применять признак Лейбница: если степенной ряд в некоторой точке x удовлетворяет признаку Лейбница, то
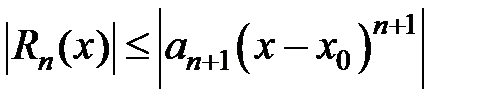 .
.
Пример 13. Вычислить число e с точностью до 0,001.
3Подставив x = 1 в формулу (12), имеем 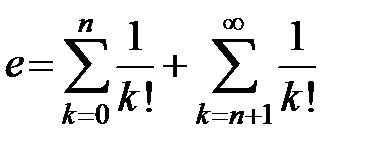 .
.
Оценим остаток
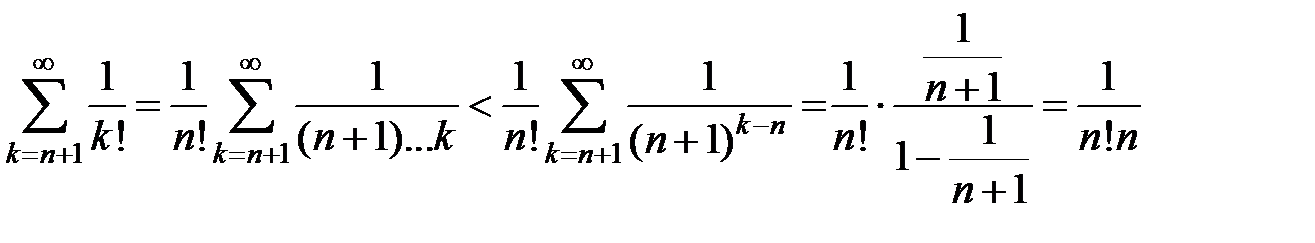 .
.
Следовательно, равенство 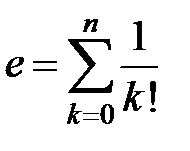 имеет абсолютную погрешность, равную
имеет абсолютную погрешность, равную 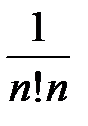 . Найдем n, для которого
. Найдем n, для которого 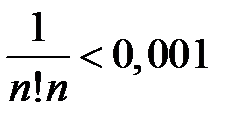 или n!n > 1000. Получаем n ³ 6. Вычисляя
или n!n > 1000. Получаем n ³ 6. Вычисляя 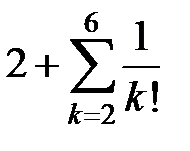 и округляя, находим ответ с требуемой точностью e » 2,718.4
и округляя, находим ответ с требуемой точностью e » 2,718.4
259. Определить, сколько нужно взять членов в разложении функции 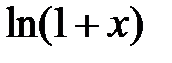 , чтобы вычислить
, чтобы вычислить 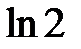 с точностью до
с точностью до 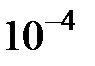 .
.
260. Определить, сколько нужно взять членов ряда в разложении функции 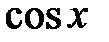 , чтобы вычислить
, чтобы вычислить 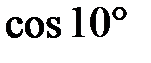 с точностью до
с точностью до 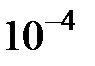 .
.
Используя соответствующие разложения, вычислить указанные значения функций с точностью до 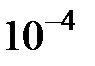 :
:
261. 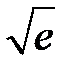 . . | 262. 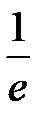 . . |
263. 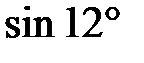 . . | 264. 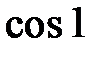 . . |
Задачи повышенной сложности
Используя соответствующие разложения, вычислить указанные значения функций с точностью до 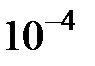 :
:
265. 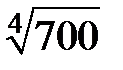 . . | 266. 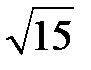 . . |
267. 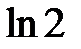 . . | 268. 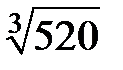 |
2) Приближенное вычисление определенных интегралов.
Разлагая подынтегральную функцию f(t) в степенной ряд, можно, используя теорему об интегрировании степенных рядов, представить интеграл 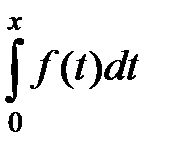 в виде степенного ряда и подсчитать величину этого интеграла с заданной точностью при любом значении
в виде степенного ряда и подсчитать величину этого интеграла с заданной точностью при любом значении 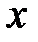 из интервала сходимости полученного ряда.
из интервала сходимости полученного ряда.
Пример 14. Разложить функцию 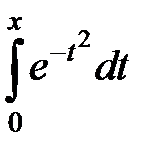 в степенной ряд по степеням x.
в степенной ряд по степеням x.
3Используя разложение 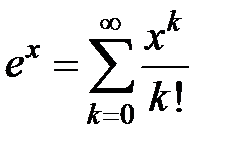 , получим
, получим 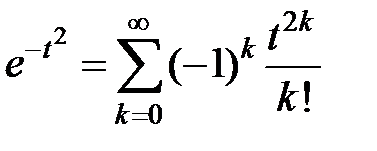 на всей числовой оси. Применяя почленное интегрирование, находим
на всей числовой оси. Применяя почленное интегрирование, находим
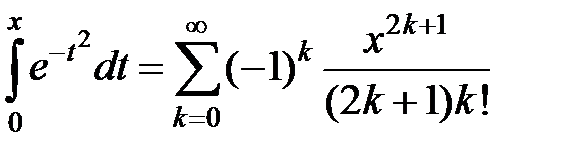 .4
.4
Пример 15. Вычислить 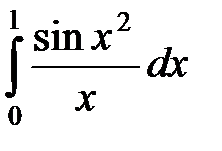 с точностью до 0,001.
с точностью до 0,001.
3Известно, что первообразная для функции 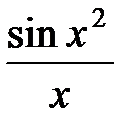 не выражается через элементарные функции. Разложим подынтегральную функцию в степенной ряд, используя разложение (31):
не выражается через элементарные функции. Разложим подынтегральную функцию в степенной ряд, используя разложение (31):
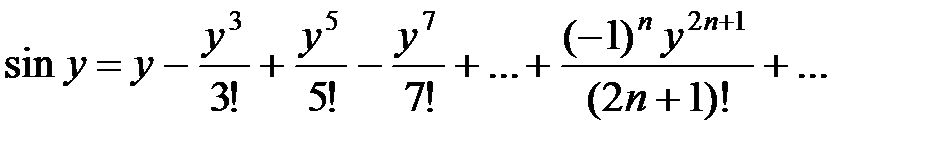
Подставляя вместо y x2, получаем
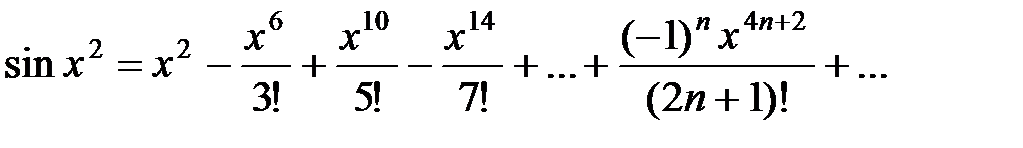
Тогда
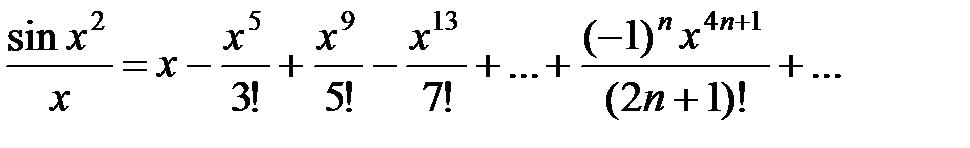
Интегрируя обе части этого равенства, получим:
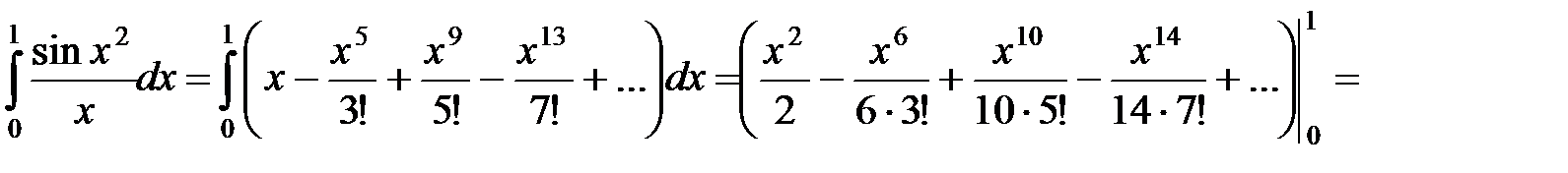
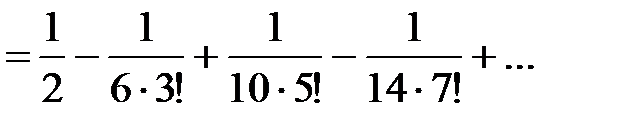
Получили знакочередующийся ряд, удовлетворяющий условиям признака Лейбница. Так как 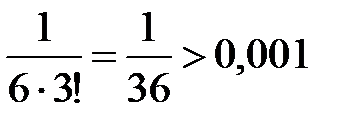 , а
, а 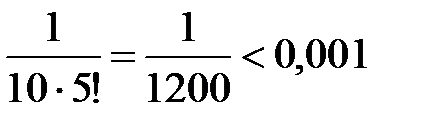 , то с точностью до 0,001 имеем
, то с точностью до 0,001 имеем
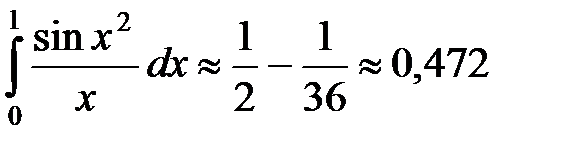 .
.
Разложить указанные функции в степенные ряды по степеням 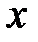 :
:
269. 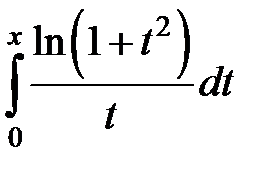 . . | 270. 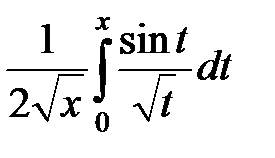 . . |
9.271. 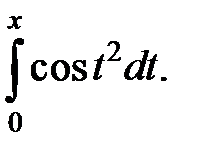 | 9.272. 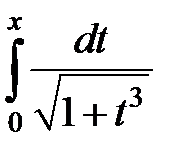 |
Вычислить интегралы с точностью до 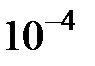 :
:
273. 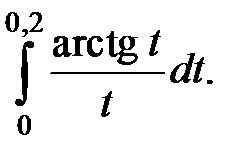 | 274. 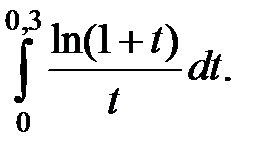 |
275. 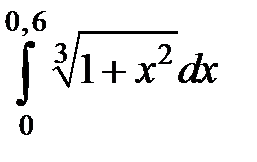 . . | 276. 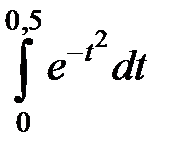 . . |
277. 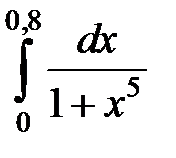 . . | 278. 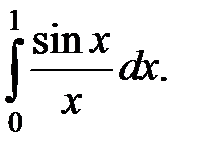 |
3) Интегрирование дифференциальных уравнений с помощью рядов.
Степенные ряды широко применяются при решении дифференциальных уравнений. Для целого ряда дифференциальных уравнений показано, что решение y(x) представимо в виде степенного ряда
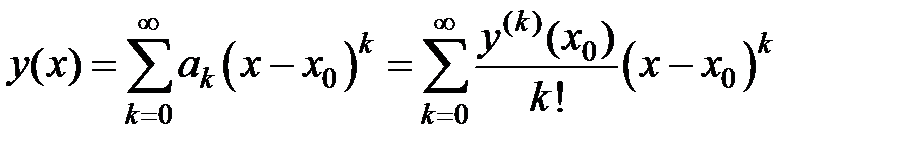 , (18)
, (18)
коэффициенты которого можно определить с учетом заданного уравнения различными способами.
а) Способ последовательного дифференцирования.
Пусть требуется найти решение уравнения y //= f(x, y, y /), удовлетворяющее условиям y(x0) = y0, y /(x0) = y1, причем функция f(x, y, y /) в точке (x0, y0, y1) имеет частные производные любого порядка. Тогда коэффициенты y (k)(x0) ряда (18) определяются путем последовательного дифференцирования исходного уравнения и подстановки в него x0и найденных уже значений y /(x0), y //(x0),…
Пример 16. Найти решение уравнения y //= x2y, удовлетворяющее условиям y(0) = 0, y /(0) = 1.
3Имеем y(0) = 0, y /(0) = 1, из заданного уравнения найдем y //(0) = 0. Далее, дифференцируя уравнение, имеем
y ///= x2y /+ 2xy,
y (4)= x2y //+ 4x y /+ 2y,
y (5)= x2y ///+ 6x y //+ 6y /,
…
y(k+2)= x2y(k)+ 2kxy(k–1)+ k(k – 1)y(k–2),
…
и при x = 0 получаем отсюда
y(k+2)(0) = k(k – 1)y(k–2)(0), k = 2,3,…
Так как y(0) = y //(0) = y ///(0) = 0 и y /(0) = 1, то
y(4n)(0) = y(4n+2)(0) = y(4n+3)(0) = 0
и
y(4n+5)(0) = (4n + 2)(4n + 3) y(4n+1)(0) = 2 × 3 × 6 × 7…(4n + 2)(4n + 3), n Î N.
Следовательно,
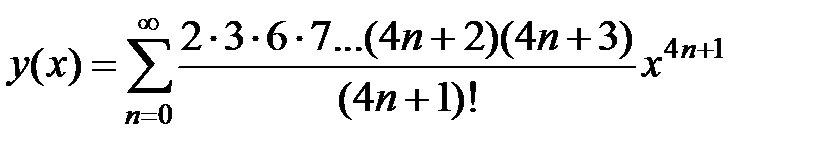 .
.
По признаку Даламбера полученный ряд сходится для любых x Î R, а определяемая этим рядом функция y(x) является решением заданного уравнения при любых x.4
б) Способ неопределенных коэффициентов.
Если исходное дифференциальное уравнение линейно относительно искомой функции и ее производных, причем коэффициент при старшей производной в точке x0отличен от нуля, то решение следует искать в виде ряда (18) с неопределенным коэффициентами ak, k = 0,1,…
Пример 17. Найти решение (в виде степенного ряда) уравнения
y //– xy /+ y = 1, удовлетворяющее условиям y(0) = y /(0) = 0.
3Ищем решение в виде ряда 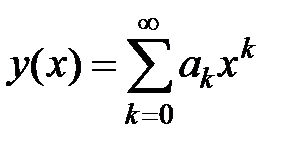 , в котором в силу условий y(0) = y /(0) = 0 имеем a0= a1= 0. Следовательно,
, в котором в силу условий y(0) = y /(0) = 0 имеем a0= a1= 0. Следовательно, 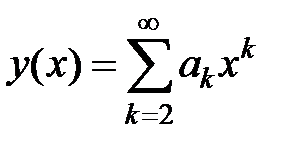 . Подставив это выражение в уравнение, получаем
. Подставив это выражение в уравнение, получаем
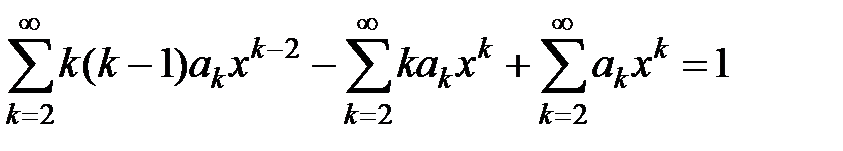 .
.
Отсюда находим, что 2 × 1 × a2= 1, т.е. 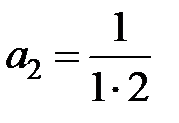 , и (k + 1)(k + 2)ak+2= =(k – 1) ak для k = 1, 2,… Так как a1= 0, то a2m+1= 0 для всех m = 0, 1,…, а для k = 2m, m = 1, 2,…, получаем рекуррентную формулу
, и (k + 1)(k + 2)ak+2= =(k – 1) ak для k = 1, 2,… Так как a1= 0, то a2m+1= 0 для всех m = 0, 1,…, а для k = 2m, m = 1, 2,…, получаем рекуррентную формулу
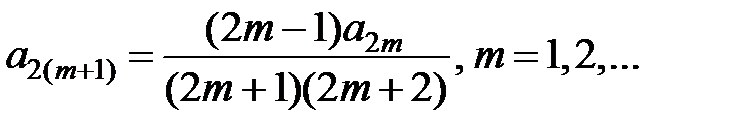 ,
,
из которой выводим равенства
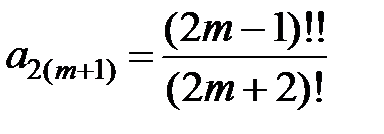 .
.
Следовательно, искомое решение имеет вид
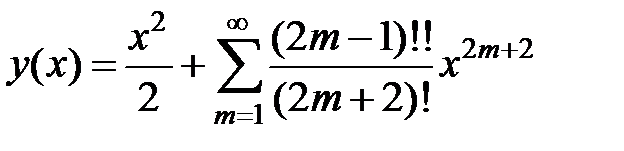 ,
,
причем полученный ряд сходится при всех x Î R.4
Найти решения уравнений, удовлетворяющие заданным условиям:
279. 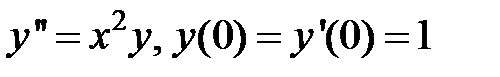 .
.
9.280. 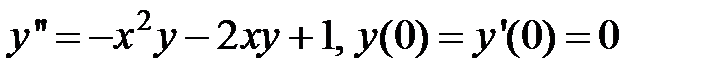 .
.
Найти первые пять членов разложения решения дифференциального уравнения в степенной ряд:
281. 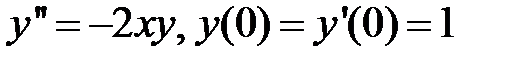 .
.
282. 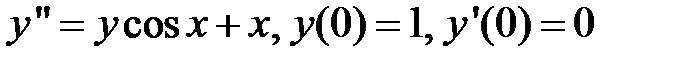 .
.
Найти решение уравнений, удовлетворяющие заданным условиям:
283. 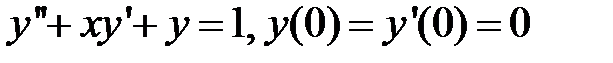 .
.
284. 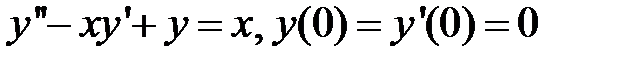 .
.
285. 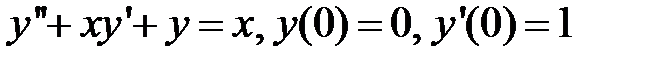 .
.
286. 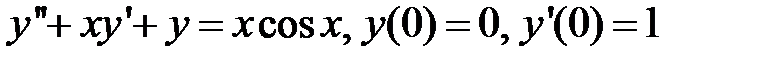 .
.
РЯДЫ ФУРЬЕ
Ряды Фурье
7.1. Тригонометрические ряды. Ортогональность тригонометрической системы
Определение.Тригонометрическим рядом называется функциональный ряд вида
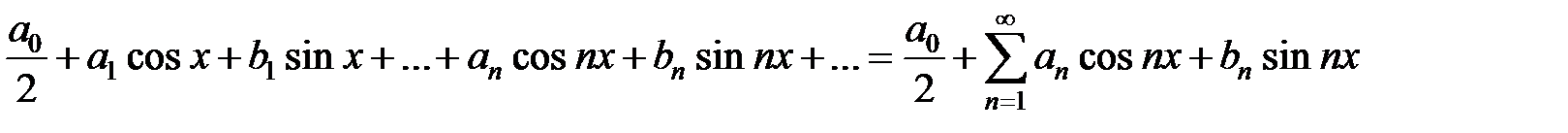 (1)
(1)
где числа a0,… an, bn(n = 1,2,…) называются коэффициентами ряда.
Теорема.Тригонометрическая система функций
1, cosx, sinx, cos2x, sin2x,…, cosnx, sinnx (2)
является ортогональной на отрезке [–p; p], т.е. интеграл по этому отрезку от произведения любых двух различных функций этой системы равен нулю, а интеграл по отрезку [–p; p] от квадрата любой функции этой системы отличен от нуля.
Доказательство. Действительно, для любых целых k, n ¹ 0 (k ¹ n) имеем:
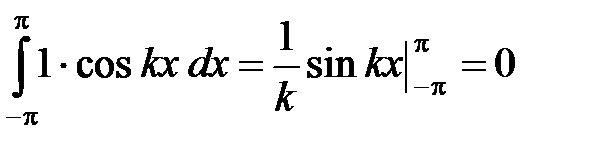 ,
, 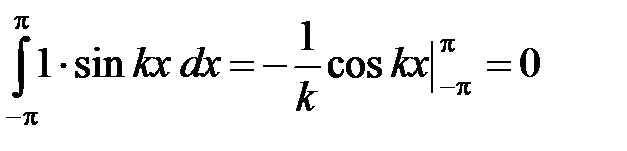 , (3)
, (3)
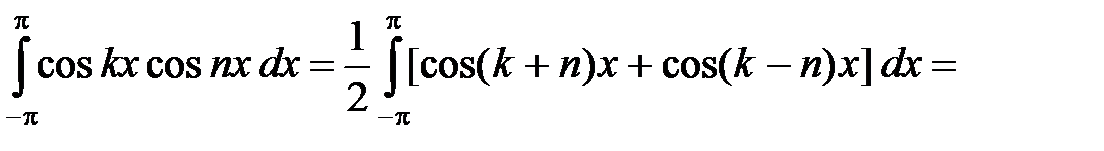
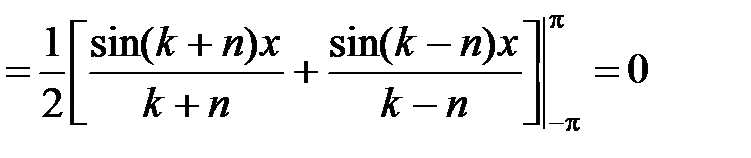 . (4)
. (4)
Аналогично
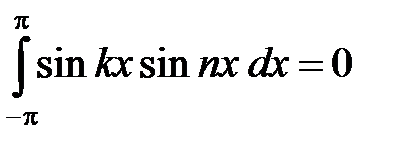 и
и 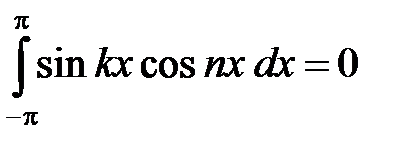 . (5)
. (5)
Наконец, 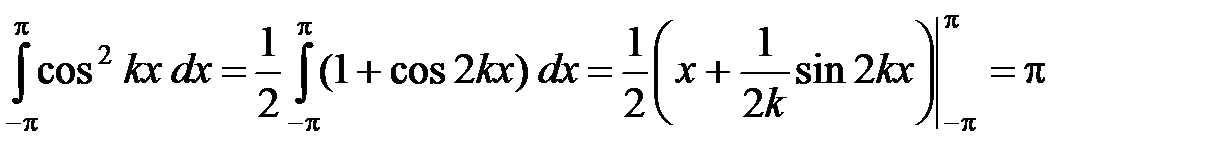 ,
,
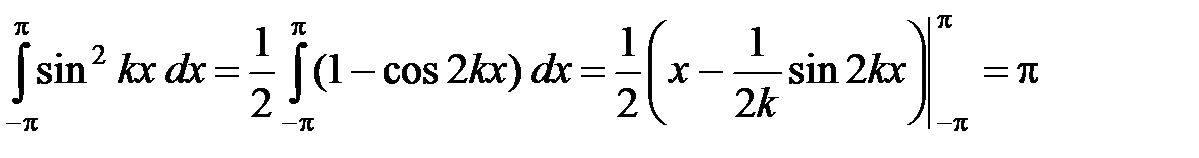 , (6)
, (6)
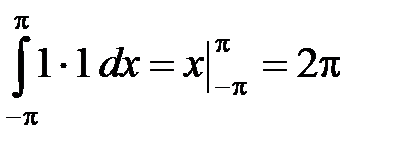 . ■
. ■
7.2. Коэффициенты Фурье. Ряд Фурье
Теорема.Если функция f(x), интегрируемая на отрезке [–p; p], разлагается в тригонометрический ряд
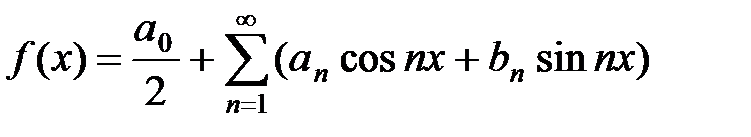 , (7)
, (7)
который можно интегрировать почленно, то это разложение единственно.
Доказательство. Интегрируя (7), получим:
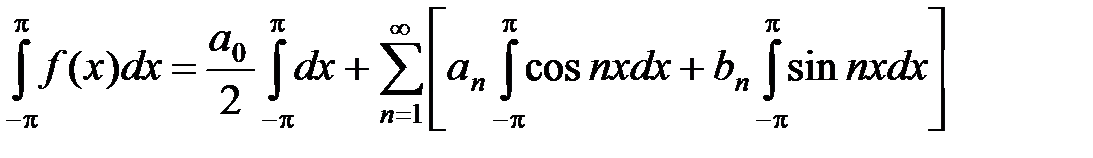 ,
,
откуда, учитывая (3), находим:
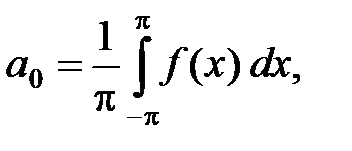 (8)
(8)
Для определения коэффициента anпри cosnx умножим равенство (7) (в котором предварительно переобозначим индекс суммирования n на k) на cosnx. Получим
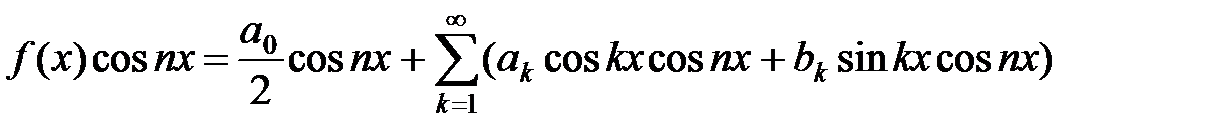 . (9)
. (9)
Т.к. каждый член этого ряда по абсолютной величине не превышает соответствующих членов ряда (7), то этот ряд тоже можно почленно интегрировать. Проинтегрируем соотношение (9) по х от –p до p. Учитывая формулы (3) – (6), получим:
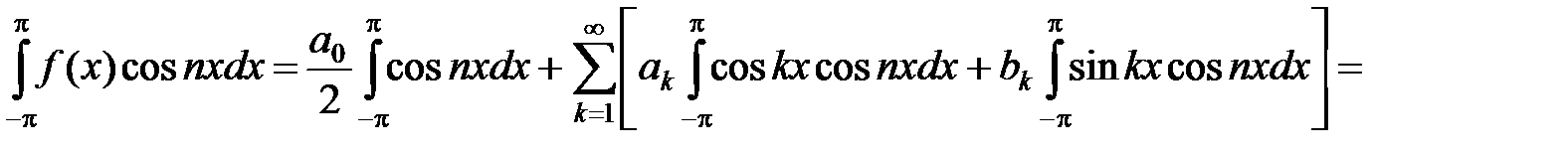
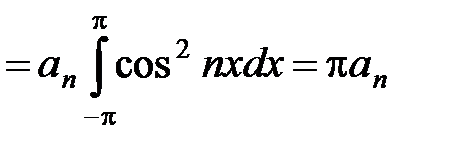 , откуда
, откуда
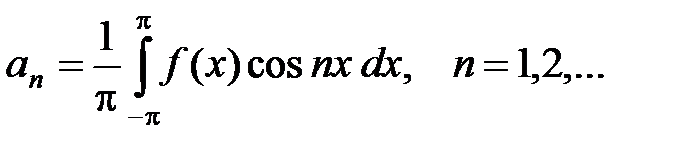 (10)
(10)
Аналогично, умножая равенство (7) на sinnx и интегрируя в пределах от –p до p, на основании тех же формул получаем
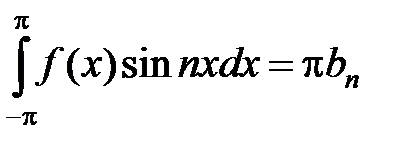 , откуда находим
, откуда находим
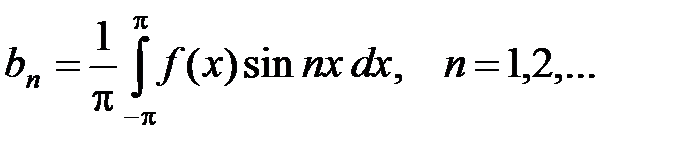 (11)
(11)
Таким образом, коэффициенты a0, an, bnряда (7) определяются по формулам (8), (10), (11) единственным образом. Теорема доказана. ■
Определение. Пусть f(x) интегрируемая на отрезке [–p; p] функция. Тогда числа a0, an, bn, найденные по формулам (8), (10), (11), называются коэффициентами Фурье функции f(x). Тригонометрический ряд (1), коэффициенты которого определяются по формулам (8), (10), (11), называется рядом Фурье функции f(x).
Для интегрируемой на отрезке [–p; p] функции f(x) записывают
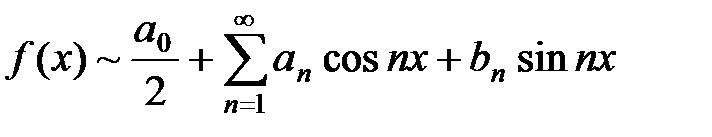
и говорят: функции f(x) соответствует (поставлен в соответствие) её ряд Фурье. Если ряд Фурье сходится, то знак соответствия заменяется знаком равенства.
7.3. Достаточное условие разложимости функции в ряд Фурье (признак Дирихле)
Определение.Функция f(x) называется кусочно-монотонной наотрезке [a, b], если этот отрезок можно разбить конечным числом точек x1, x2,…, xn–1на интервалы (a, x1), (x1, x2),…, (xn–1, b) так, что на каждом из интервалов функция монотонна.
Заметим, что если функция f(x) кусочно-монотонная и ограниченная на отрезке [a, b], то она может иметь точки разрыва только первого рода.
Теорема (Признак Дирихле). Если 2p периодическая функция f(x) является кусочно-монотонной и ограниченной на отрезке [–p; p] , то её ряд Фурье сходится во всех точках. Сумма этого ряда равна значению функции f(x) в точках непрерывности функции и значению 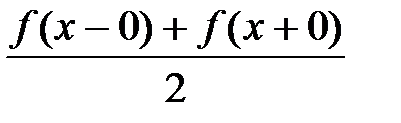 в точках разрыва.
в точках разрыва.
7.4. Разложение в ряд Фурье четных и нечетных функций
1) Пусть функция f(x) определена на отрезке [–p; p]. Если функция четная, т.е. f(–x) = f(x), то её ряд Фурье имеет вид
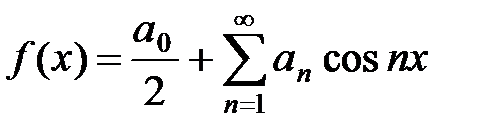 , (12)
, (12)
где 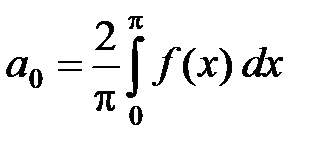 ,
, 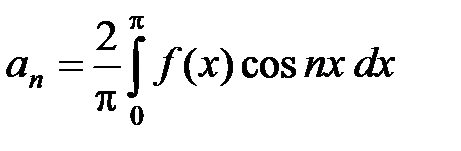 , n Î N,
, n Î N,
а коэффициенты Фурье bn= 0.
Действительно,
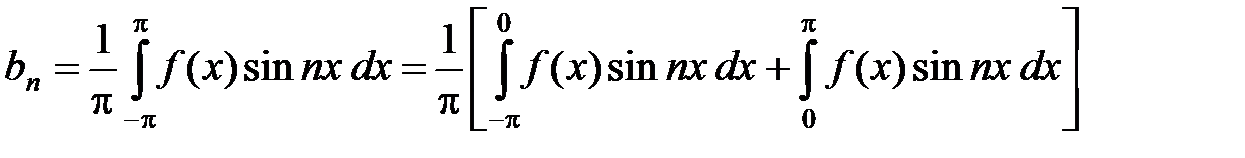 .
.
В первом интеграле в квадратных скобках сделаем замену переменной x = – t. Тогда dx = – dt, а пределы интегрирования станут от p до 0. Принимая во внимание, что функция f(x) – четная, а функция sin x – нечетная, получаем
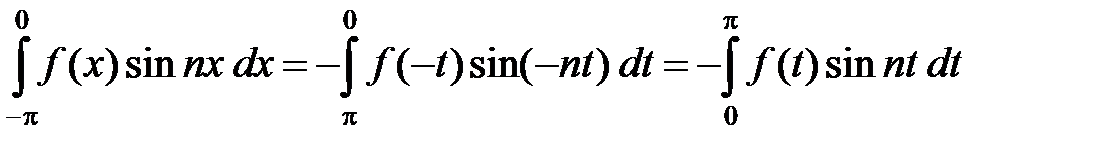 .
.
Следовательно, 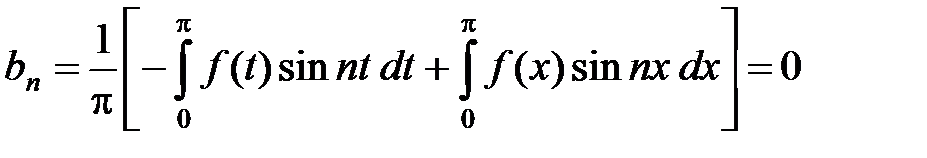 .
.
Аналогично, учитывая, что функции f(x) и cos х четные, можно получить записанные выше выражения для коэффициентов аn.
2) Пусть теперь функция f(x), определенная на отрезке [–p; p], нечетная, т.е. f(–x) = –f(x) то её ряд Фурье имеет вид
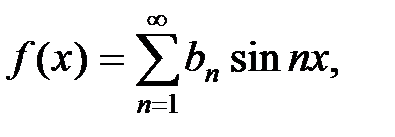
где 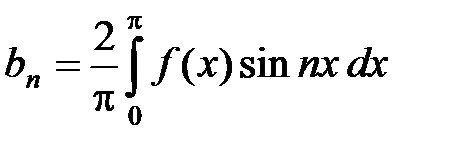 , n Î N, (13)
, n Î N, (13)
а коэффициенты Фурье аn= 0.
Рассуждения здесь такие же, как и в случае 1).
Таким образом, если функция f(x) четная, то ряд Фурье содержит только косинусы, а если нечетная, то только синусы.
| y |
| x |
| p |
| –p |
| 2p |
| –2p |
| –1 |
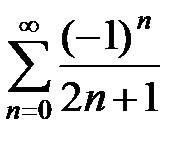 .
. 3Продолжая периодически функцию f(x) на всю вещественную ось, получим функцию 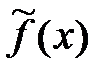 , график которой изображен на рисунке. Эта функция 2p-периодическая, кусочно-монотонная и ограниченная, значит, согласно признаку Дирихле она разложима в ряд Фурье. Вычислим коэффициенты Фурье функции f(x). Так как функция нечетная, то an= 0, n = 0,1,…, а коэффициенты bnнаходится по формуле (13):
, график которой изображен на рисунке. Эта функция 2p-периодическая, кусочно-монотонная и ограниченная, значит, согласно признаку Дирихле она разложима в ряд Фурье. Вычислим коэффициенты Фурье функции f(x). Так как функция нечетная, то an= 0, n = 0,1,…, а коэффициенты bnнаходится по формуле (13):
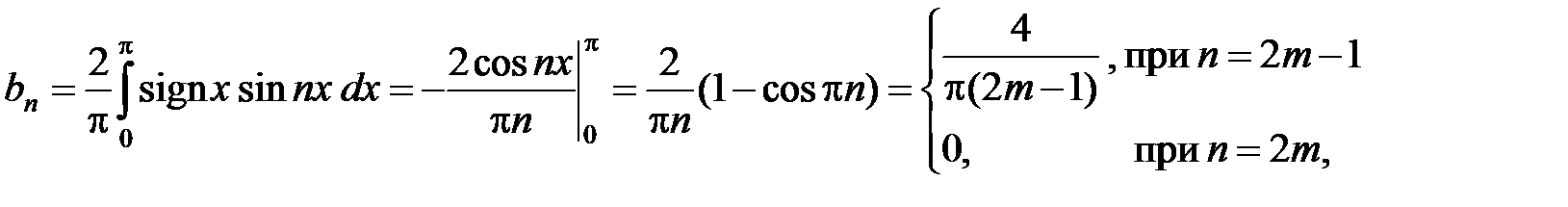
где m Î N. Следовательно, при –p < x < p
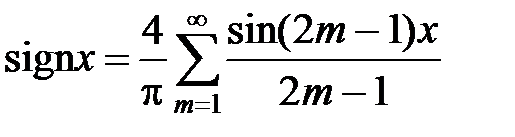 ,
,
откуда при 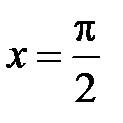 получаем
получаем 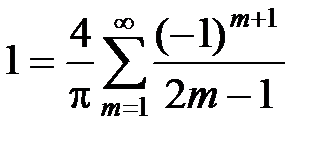 , т.е.
, т.е. 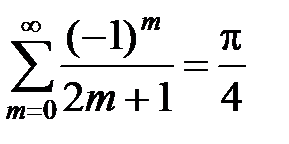 .
.
Отметим, что вне интервала (–p; p) полученный ряд сходится к функции  : в точках непрерывности функции
: в точках непрерывности функции  ряд Фурье будет сходиться к значению функции в этой точке, а в точках разрыва x = pn, где n Î Z, функция
ряд Фурье будет сходиться к значению функции в этой точке, а в точках разрыва x = pn, где n Î Z, функция 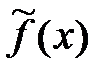 не определена, а сумма ряда Фурье равна нулю.4
не определена, а сумма ряда Фурье равна нулю.4
Пример 2. Разложить в ряд Фурье функцию f(x) = x2на отрезке [–p; p].
| y |
| x |
| p |
| –p |
| 3p |
| –3p |
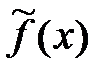 , график которой изображен на рисунке. Эта функция 2p-периодическая, непрерывная и ограниченная, следовательно, может быть разложена в ряд Фурье. Так как она четная, то её коэффициенты Фурье bn= 0, а anнаходится по формулам (11):
, график которой изображен на рисунке. Эта функция 2p-периодическая, непрерывная и ограниченная, следовательно, может быть разложена в ряд Фурье. Так как она четная, то её коэффициенты Фурье bn= 0, а anнаходится по формулам (11): 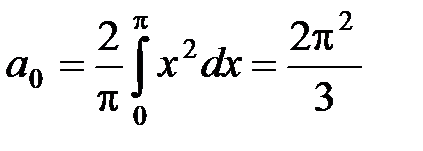 ,
,
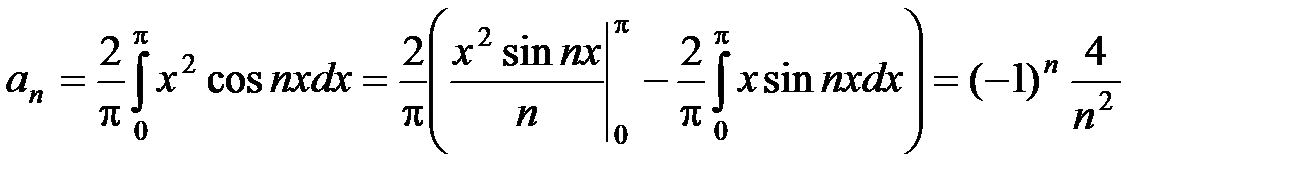 .
.
Значит, ряд Фурье данной функции имеет вид
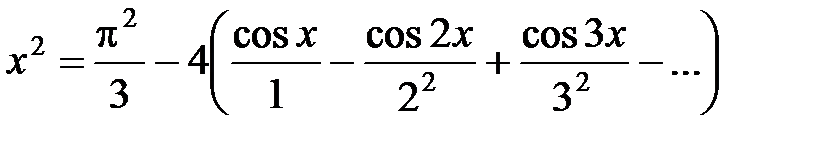 .
.
Это разложение справедливо для любого x Î [–p; p], так как в данном случае в точках x = ±p сумма ряда совпадает со значениями функции f(x) = x2, поскольку 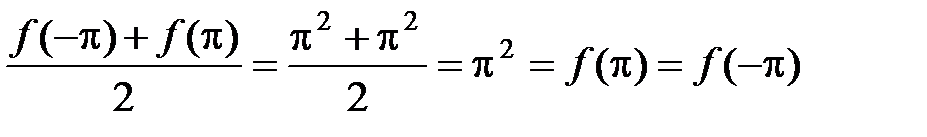 .
.
В силу непрерывности функции  для всех значений х Î R ее ряд Фурье в любой точке будет сходиться к значению функции в этой точке.4
для всех значений х Î R ее ряд Фурье в любой точке будет сходиться к значению функции в этой точке.4
7.5. Разложение в ряд Фурье функций с произвольным периодом
Пусть теперь функция f(x) является периодической с произвольным периодом 2l, l ¹ 0. Отметим, что признак Дирихле, сформулированный в п. 7.4, для 2p-периодических функций, справедлив и для функций с произвольным периодом.
Пусть функция f(x) интегрируема на отрезке [–l; l] (где l > 0). Тогда ряд Фурье функции f(x) имеет вид
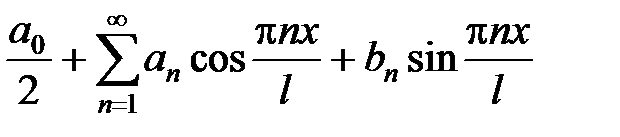 , (14)
, (14)
где 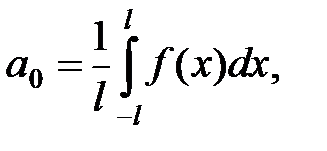
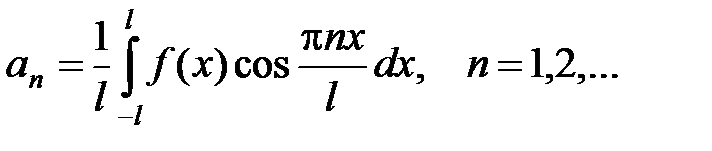 ,
,
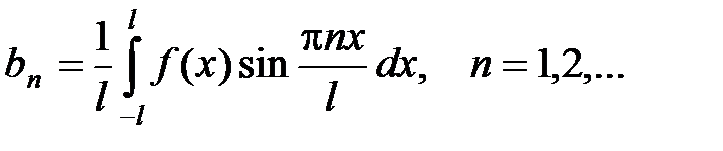
Если функция f(x), кроме того, непрерывна, то
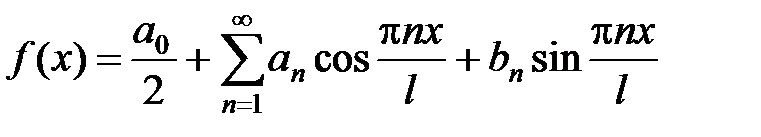 .
.
Для доказательства (14) сделаем замену переменной 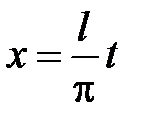 . Тогда функция
. Тогда функция 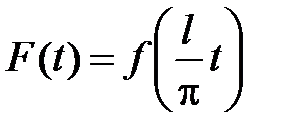 будет периодической функцией аргумента t с периодом 2p, так как
будет периодической функцией аргумента t с периодом 2p, так как
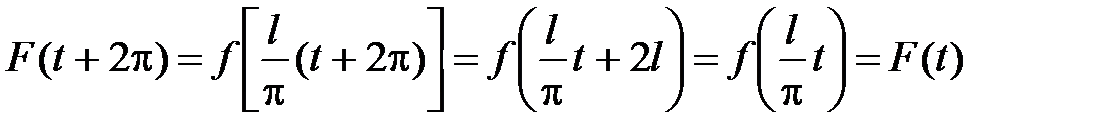 ,
,
и ее можно разложить на отрезке [–p; p] в ряд Фурье
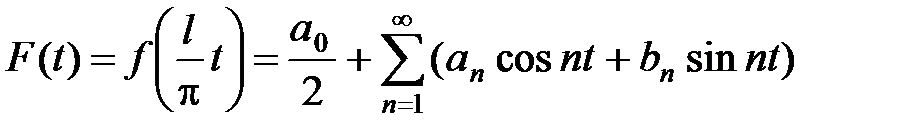 ,
,
где
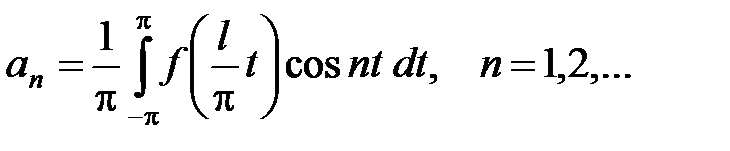
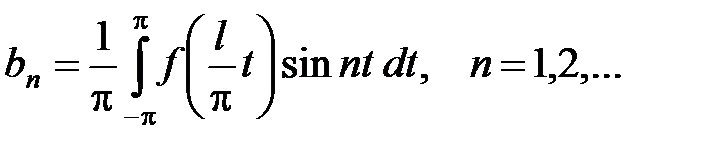
Возвращаясь к переменной х, т.е. положив 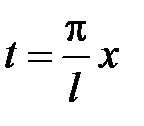 ,
, 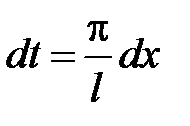 , получим ряд (14) с соответствующими коэффициентами.
, получим ряд (14) с соответствующими коэффициентами.
Пример 3. На отрезке [–3; 3] найти тригонометрический ряд Фурье функции f(x) = |x|.
| y |
| x |
| –6 |
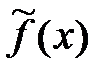 , график которой изображен на рисунке. Эта функция периодическая с периодом 2l = 6, непрерывная и ограниченная, следовательно, может быть разложена в ряд Фурье. Кроме того, функция f(x) = |x| – четная, следовательно, все коэффициенты Фурье bn= 0, а коэффициенты аnвычисляются следующим образом:
, график которой изображен на рисунке. Эта функция периодическая с периодом 2l = 6, непрерывная и ограниченная, следовательно, может быть разложена в ряд Фурье. Кроме того, функция f(x) = |x| – четная, следовательно, все коэффициенты Фурье bn= 0, а коэффициенты аnвычисляются следующим образом: 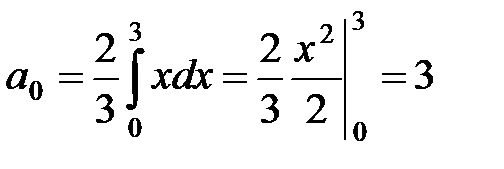 ,
,
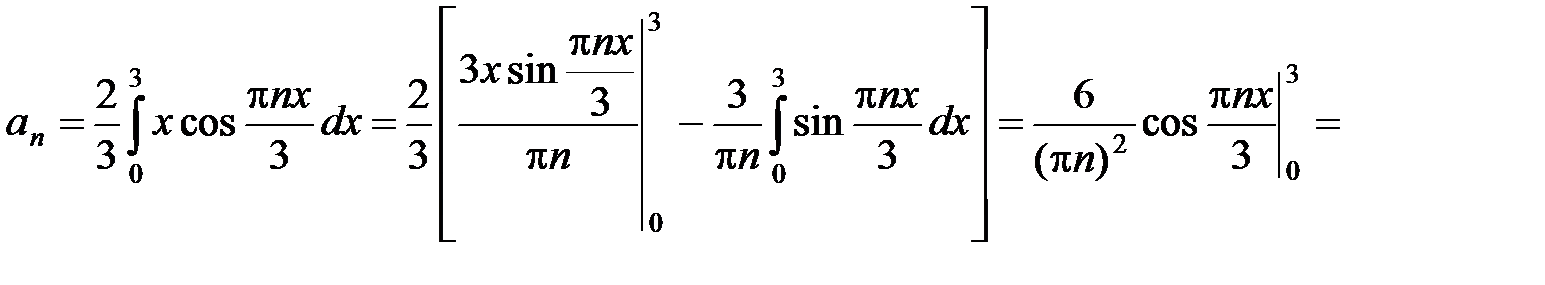
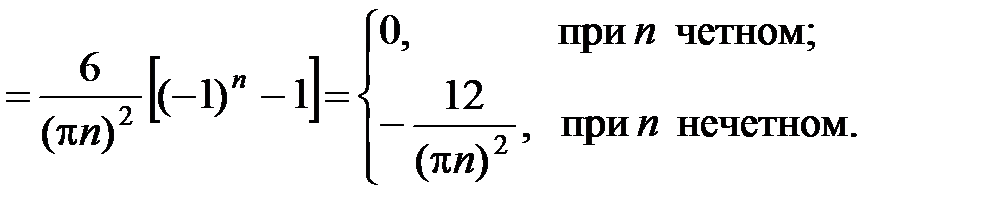
Тогда ряд Фурье функции f(x) на отрезке [–3; 3] имеет вид:
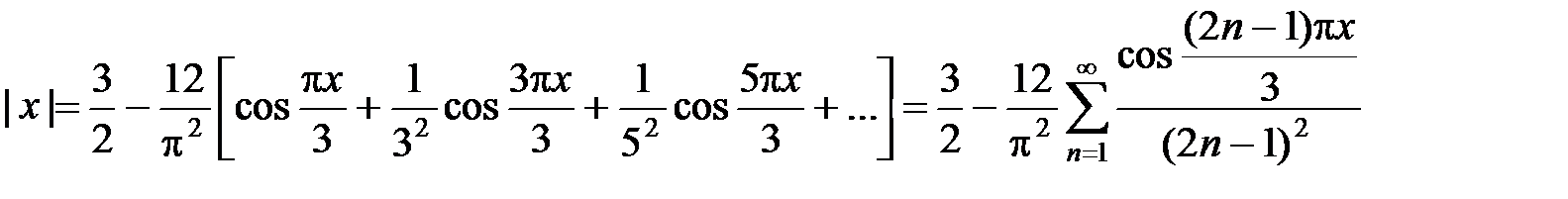 .
.
Так как функция 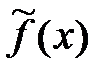 удовлетворяет условиям признака Дирихле, то ряд Фурье этой функции во всех точках сходится к значению функции.4
удовлетворяет условиям признака Дирихле, то ряд Фурье этой функции во всех точках сходится к значению функции.4
287. Доказать, что ряд Фурье тригонометрического многочлена 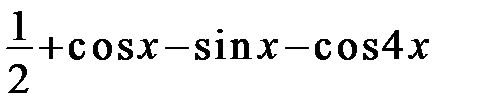 совпадает с этим многочленом.
совпадает с этим многочленом.
288. Доказать, что ряд Фурье тригонометрического многочлена 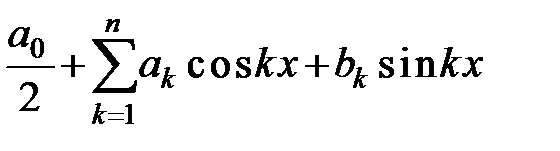 совпадает с этим многочленом.
совпадает с этим многочленом.
289. Найти коэффициент 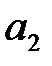 Фурье функции
Фурье функции 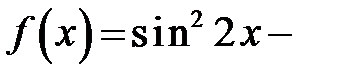
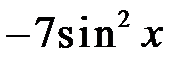 .
.
9.290. Найти коэффициент 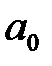 Фурье функции
Фурье функции 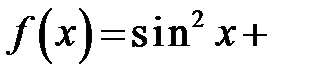
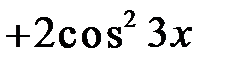 .
.
291. Разложить в ряд Фурье функцию 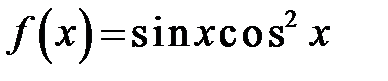 .
.
292. Разложить в ряд Фурье функцию 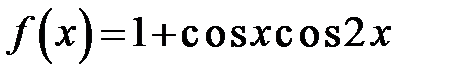 .
.
293. Вычислить коэффициент 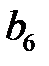 Фурье периодической с периодом
Фурье периодической с периодом 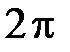 функции
функции 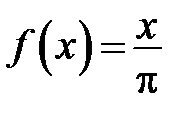 ,
, 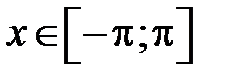 .
.
294. Вычислить коэффициент 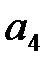 Фурье периодической с периодом
Фурье периодической с периодом 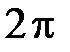 функции
функции 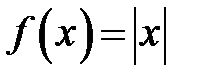 ,
, 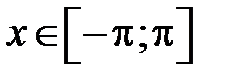 .
.
295. Вычислить коэффициент 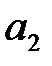 Фурье периодической с периодом 3 функции
Фурье периодической с периодом 3 функции 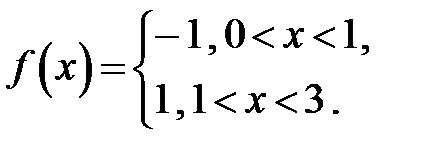
296. Вычислить коэффициент 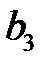 Фурье периодической с периодом 2 функции
Фурье периодической с периодом 2 функции 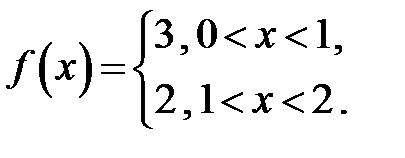
297. Доказать, что если f(x) имеет период 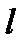 , то
, то 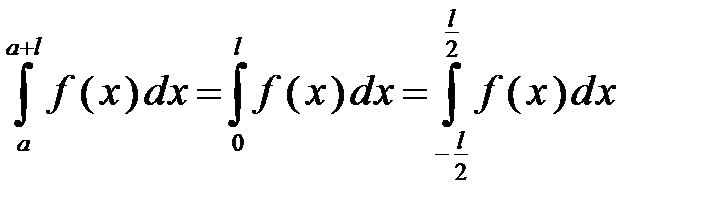 при любом
при любом 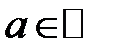 .
.
298. Записать выражение коэффициентов Фурье (28) - (30) для четной и нечетной функций на 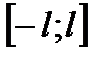 .
.
Разложить 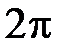 - периодичную функцию в ряд Фурье и найти значение
- периодичную функцию в ряд Фурье и найти значение 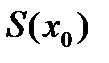 суммы полученного ряда в заданной точке
суммы полученного ряда в заданной точке 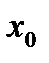 .
.
299. 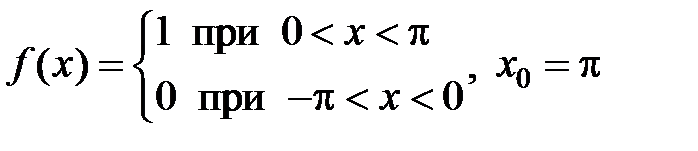 .
.
300. 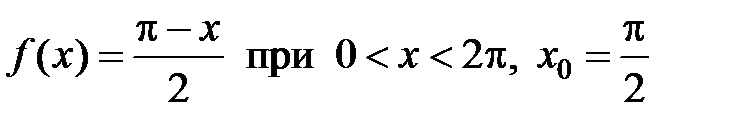 .
.
301. Разложить в ряд Фурье функцию 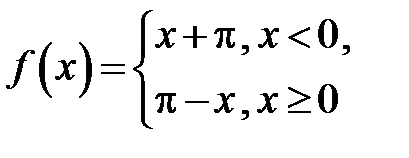 в промежутке
в промежутке 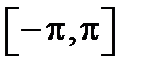 и построить график суммы ряда Фурье этой функции.
и построить график суммы ряда Фурье этой функции.
302. Разложить в ряд Фурье функцию 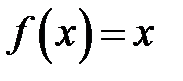 в интервале
в интервале 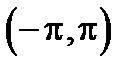 и построить график суммы ряда Фурье этой функции.
и построить график суммы ряда Фурье этой функции.
Разложить в ряд Фурье следующие функции периода 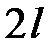 :
:
303. 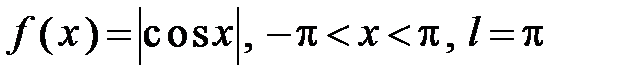 .
.
304. 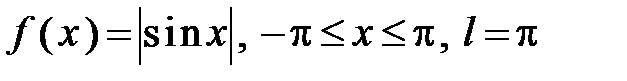 .
.
305. 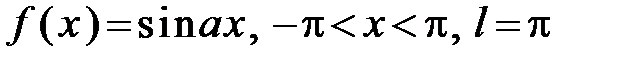 .
.
306. 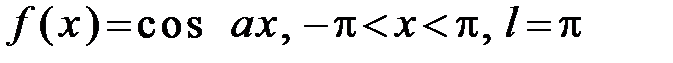 .
.
307. 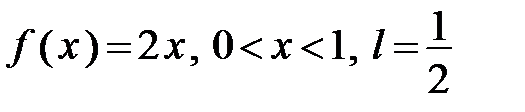 .
.
308. 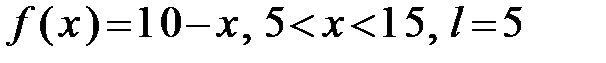 .
.
309. Разложить в ряд Фурье в интервале 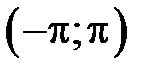 функцию
функцию 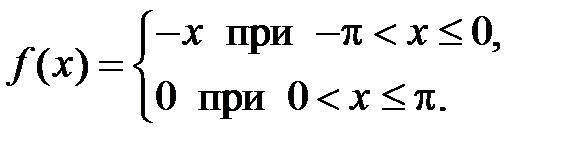
310. Разложить в ряд Фурье в интервале 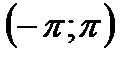 функцию
функцию 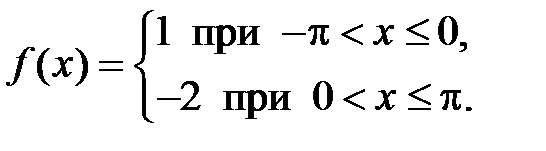
311. Доказать равенство 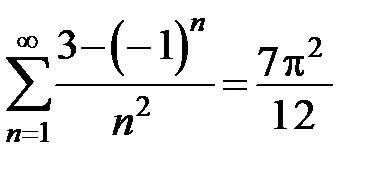 , используя разложение в ряд Фурье функции
, используя разложение в ряд Фурье функции 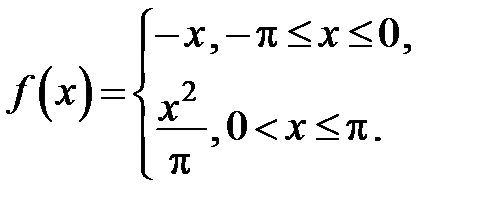
312. Доказать равенство 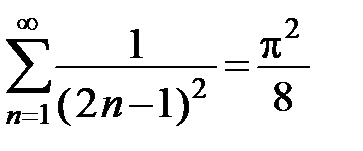 , используя разложение в ряд Фурье функции
, используя разложение в ряд Фурье функции 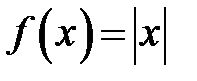 ,
, 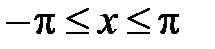 .
.
313. Используя ряд Фурье, полученный в задаче 9.304, найти сумму ряда 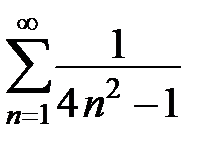 .
.
314. Используя разложение функции 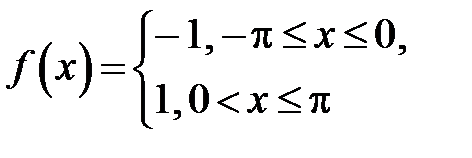 в ряд Фурье, найти сумму ряда
в ряд Фурье, найти сумму ряда 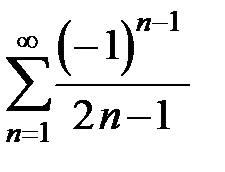 .
.
СПИСОК ЛИТЕРАТУРЫ
1. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. Том 1. – М.: Наука, 2010.
2. Кудрявцев Л.Д. Курс математического анализа. Том 1. – М.: Высшая школа, 1981.
3. Тер-Крикоров А.М., Шабунин М.И. Курс математического анализа. М.: Наука, 1988.
4. Никольский С.М. Курс математического анализа. Том 1. – M.: Наука, 1990.
5. Власова Е.А. Ряды. Том IX. – М.: Изд-во МГТУ им. Н.Э. Баумана. 2000.
6. Шипачев В.С. Высшая математика. – М.: Высшая школа, 2010.
7. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Том 2. – М.: Наука, 2010.
8. Беляева, М.А. Ряды. Методические указания к практическим занятиям и к выполнению расчетного задания / М.А.Беляева, А.Г.Мясников, Т.А.Мацеевич. М.: Изд-во МГСУ, 2003.
9. Титова, Т.Н. Числовые и функциональные ряды. Учебное пособие / Т.Н.Титова, Т.А.Мацеевич, Е.Е. Ассеева и др. М.: Изд-во НИУ МГСУ, 2017. 128 с.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Б
Бином Ньютона, 62
И
Интервал сходимости степенного ряда, 46
К
Коэффициенты
степенного ряда, 43
тригонометрического ряда, 70
Фурье, 72
Критерий Коши сходимости ряда, 9
Круг сходимости степенного ряда, 46
Н
Необходимое условие сходимости, 7
О
Область
абсолютной сходимости функционального ряда, 33
сходимости функционального ряда, 33
Остаток
ряда, 9
функционального ряда, 33
П
Признак
Даламбера, 16
Дирихле, 73
Коши, 18
Коши интегральный, 20
Лейбница, 26
равномерной сходимости функционального ряда Вейерштрасса, 36
сравнения, 11
сравнения предельный, 14
Р
Радиус сходимости степенного ряда, 46
Ряд
абсолютно сходящийся, 25
биномиальный, 62
гармонический, 9
Дирихле, 23
знакопеременный, 24
знакочередующийся, 26
из членов геометрической прогрессии, 5
мажорируемый, 35
мажорирующий, 36
Маклорена, 54
расходящийся, 5
с неотрицательными членами, 11
степенной, 43
сходящийся, 5
Тейлора, 54
тригонометрический, 70
условно сходящийся, 28
функциональный, 32
функциональный равномерно сходящийся, 35
Фурье, 72
числовой действительный, 5
числовой комплексный, 5
Ряды
применение степенных рядов, 64
С
Свойства сходящихся рядов, 9
Сумма
ряда, 5
функционального ряда, 33
частичная, 5
Сходимость
абсолютная функционального ряда, 32
функционального ряда в точке, 32
функционального ряда на множестве, 32
Т
Теорема
Абеля, 44
достаточное условие разложимости в ряд Тейлора, 57
достаточное условие сходимости знакопеременного ряда, 24
необходимое и достаточное условие разложимости в ряд Тейлора, 56
о дифференцировании степенных рядов, 53
о единственности разложения функции в степенной ряд, 55
о непрерывности суммы ряда, 38
о почленном дифференцировании ряда, 41
о почленном интегрировании ряда, 39
об интегрировании степенных рядов, 52
Римана, 29
Тригонометрическая система функций, 70
Ф
Функция
кусочно-монотонная, 73
Ц
Центр степенного ряда, 43
Ч
Член
функционального ряда, 32
ОТВЕТЫ
1. 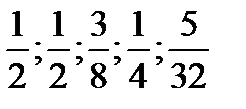 . 2.
. 2. 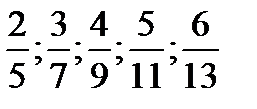 . 3.
. 3. 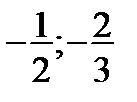 . 4.
. 4. 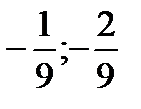 . 5.
. 5. 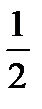 . 6.
. 6. 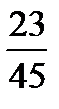 . 7.
. 7.
