Связь дифференцируемости с существованием конечной производной. Связь непрерывности и дифференцируемости функции.
Связь дифференцируемости с существованием конечной производной. Связь непрерывности и дифференцируемости функции.
(связь дифференцируемости с существованием производной)
Функция y = f(x) дифференцируема в точке xÎD(f) тогда и только тогда, когда она имеет в этой точке производную f '(x). При этом f '(x) = A.
(связь непрерывности и дифференцируемости функции)
если функция y=f(x) дифференцируема на некотором интервале, то она и непрерывна на этом интервале.
Основные правила дифференцирования: производная постоянной, суммы, произведения и частного. Производная сложной и обратной функций.
Производная обратной функции :
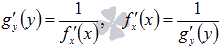
4. Геометрический смысл (а) бесконечной производной; (б) односторонних производных.
Геометрический смысл бесконечной производной состоит в следующем: если производная f '( x0)= ¥ то касательная к графику функции f(x) в точке x0 параллельна оси Oy и описывается уравнением х=х0
Геометрическое истолкование производной как углового коэффициента касательной распространяется и на случай бесконечной производной; но здесь — касательная оказывается параллельной оси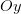 
.
Механический смысл первой и второй производной
6. Правила вычисления дифференциала суммы, произведения и частного двух функций.
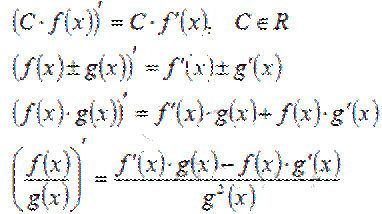
7. Свойство инвариантности первого дифференциала
Дифференциал функции имеет один и тот же вид: произведение производной по некоторой переменной на дифференциал этой переменной - независимо от того, является ли эта переменная, в свою очередь, функцией другой переменной или она является независимой переменной.
8. Формулы для вычисления дифференциалов высших порядков
Теорема Ферма
10. Теорема Ролля. Теорема Лагранжа. Теорема Коши. Геометрическая интерпретация теорем Ролля и Лагранжа.
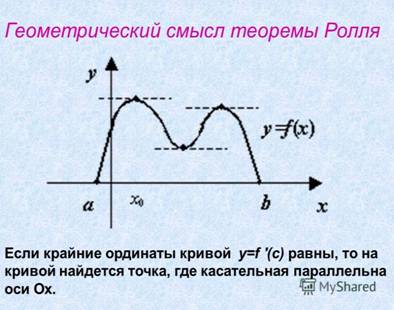
Теорема Ролля
Пусть функция f (x) непрерывна на [a, b], дифференцируема на (a, b) и на концах отрезка принимает равные значения f(a) = f(b). Тогда существует точка c Î (a, b), в которой f ' (c) = 0.
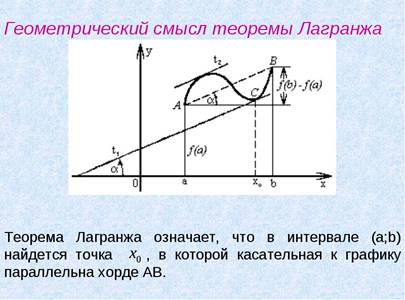
Теорема Лагранжа
Если функция f(x) непрерывна на замкнутом отрезке [a, b], дифференцируема внутри него, то существует такая точка с Î (a, b), что выполняется равенство
f(b) − f(a) = f '(c)·(b − a).
Теорема Коши
Пусть функции f (x) и g(x) непрерывны на [a, b] и дифференцируемы на (a, b). Пусть, кроме того, во всех точках интервала (a, b) функция g(x) имеет ненулевую производную g ' (x) ≠ 0. Тогда существует точка c Î (a, b), такая, что справедлива формула
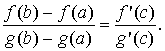
11.Правило Лопиталя 
12. Сравнение роста показательной,степенной и логарифмической функций.
при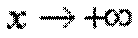 
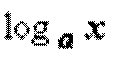(логарифмическая функция)= о( 
), 
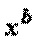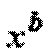(степенная функция)=о( 
) ( 
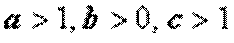), т.е. при 
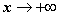ББ функция 
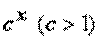(показательная) имеет более высокий порядок роста, чем ББ функции 
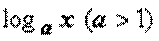и 
; ББ функция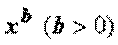 
имеет более высокий порядок роста, чем ББ функция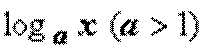 
13 (основное свойство многочлена Тейлора) Пусть функцияy=f(x) –n– раз дифференцируема в точке х0f(x)=Tn(x0);f’(x0)=Tn’(x0),…,f(n)(x0)=Tn(n)(x0)
Связь дифференцируемости с существованием конечной производной. Связь непрерывности и дифференцируемости функции.
(связь дифференцируемости с существованием производной)
Функция y = f(x) дифференцируема в точке xÎD(f) тогда и только тогда, когда она имеет в этой точке производную f '(x). При этом f '(x) = A.
(связь непрерывности и дифференцируемости функции)
если функция y=f(x) дифференцируема на некотором интервале, то она и непрерывна на этом интервале.