Приближенное решение с использованием аппроксимаций и продольных, и поперечных перемещений

Для упрощения расчетов применяют приближенные решения. Для этого аппроксимируем перемещения. Представим их в следующем виде:

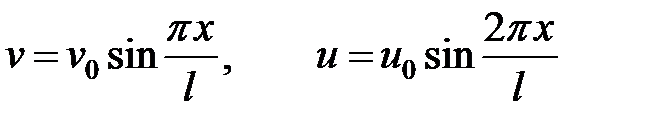(11)

Здесь 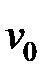- прогиб в центре балки.

Тогда на уровне центра тяжести сечения

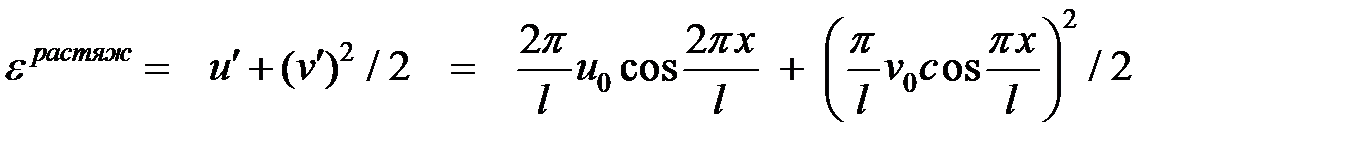(12)

Вновь считаем, что усилия растяжения, а значит и продольная деформация на уровне центра тяжести постоянны по всей длине балки:

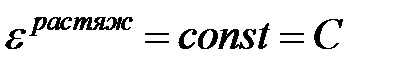
Тогда справедливо и соотношение

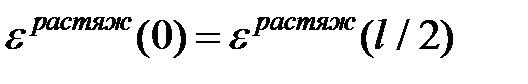
Подставляя сюда формулу (12) можно найти связь 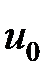с прогибом :

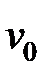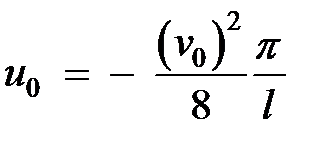(13)

Изгибные деформации вычисляются как обычно

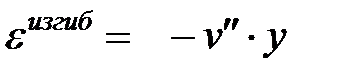
Полная деформация будет

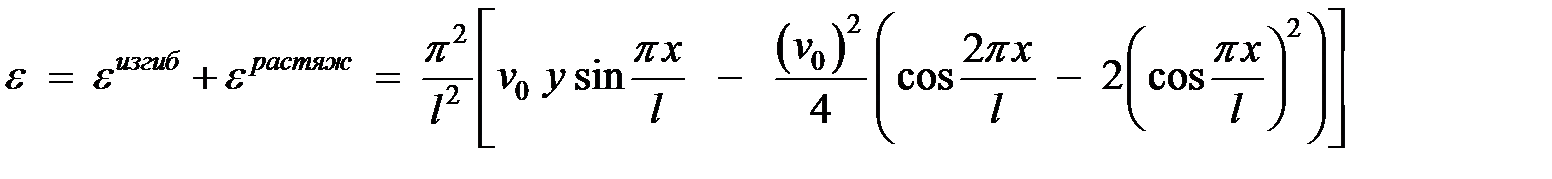(14)

Напряжения теперь вычисляются через прогиб :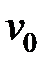

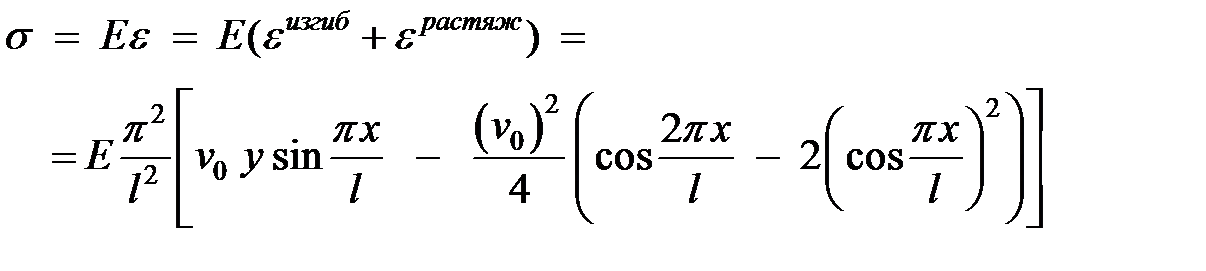(15)

Для того, чтобы найти зависимость прогиба 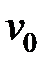от нагрузки q, используем закон сохранения энергии в варианте принципа возможных перемещений.

Пусть произошло увеличение 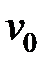на малую величину 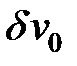. Тогда новые перемещения будут

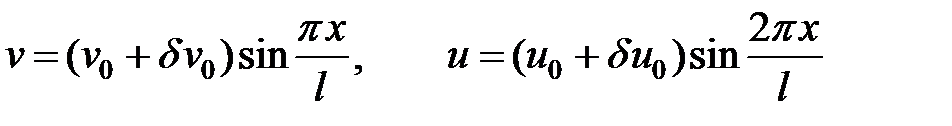(16)

Деформации вырастут на следующую величину

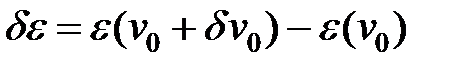(17)

Подставляя сюда выражения для деформаций (14) получим

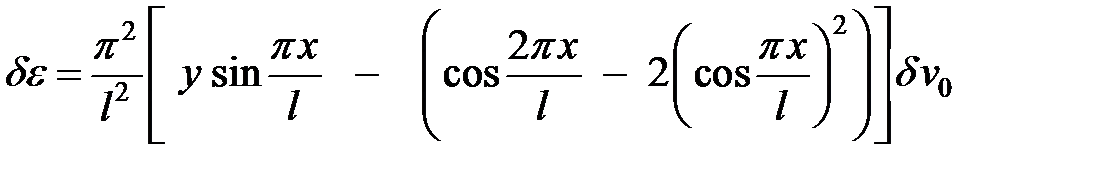(18)

Вычислим работу напряжений на этих малых деформациях (V – это объем балки):

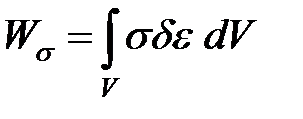(19)

Работа нагрузки будет

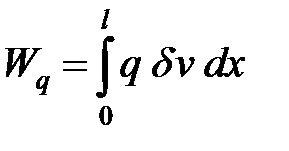(20)

Из условия равенства этих работ получим выражение для нагрузки q, выраженной через перемещение центра балки :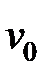

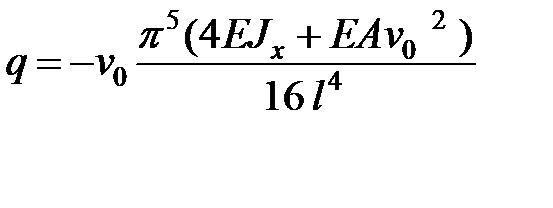` (21)

Здесь второе слагаемое в скобках появляется ввиду учета жесткости балки на растяжение АЕ.

Значит, нелинейность начинает проявляться только тогда, когда прогиб центра балки имеет такую величину, при которой

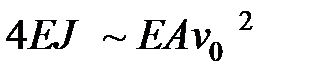
Отсюда видно, что для обеспечения погрешности не более 5% нужно, чтобы максимальный прогиб 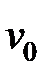удовлетворял условию

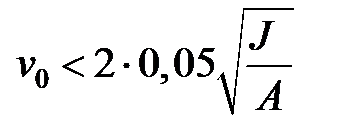
Поскольку 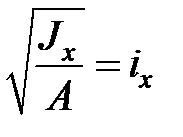, то можно сделать вывод о применимости в этой задаче линейной теории лишь в том случае, когда прогиб меньше радиуса инерции сечения в десять раз. Например, для прямоугольного сечения 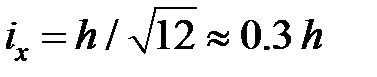. Таким образом, в случае абсолютно жестких шарнирных опор линейная теория применима только тогда, когда прогиб составляет не более 3% от толщины балки. Однако в реальных объектах абсолютно жесткого закрепления не существует, оно всегда будет иметь податливость. Поэтому полученное решение имеет лишь теоретическое значение. Учет даже упругой податливости опор увеличивает трудности точоного решения задачи, но оно может быть снова получено приближенными методами с гораздо меньшими затратами труда.

Приближенное решение с использованием аппроксимации только поперечных перемещений

Еще более простое решение получим, если аппроксимируем только прогиб, считая что продольные пермещения настолько малы, что ими можно пренебречь. Представим их в виде, при котором удовлетворяются условия закрепления:

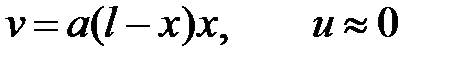(22)

Здесь a - искомая константа.

Тогда

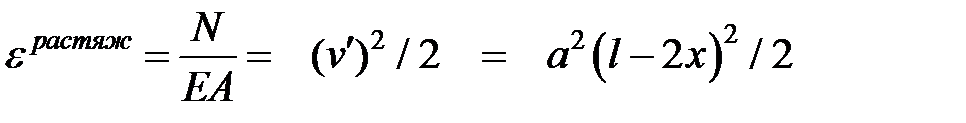(23)

Для того, чтобы найти зависимость a от нагрузки q, снова используем закон сохранения энергии в варианте принципа возможных перемещений.

Пусть произошло увеличение a на малую величину 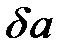. Тогда изменения кривизны 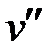балки и осевых деформаций растяжения 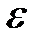вырастут на следующие величины

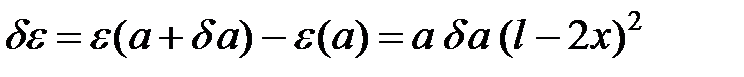(24)

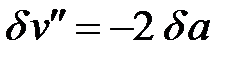
Вычислим работу силы 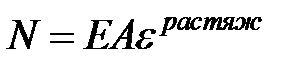и изгибающего момента 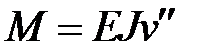на этих малых деформациях:

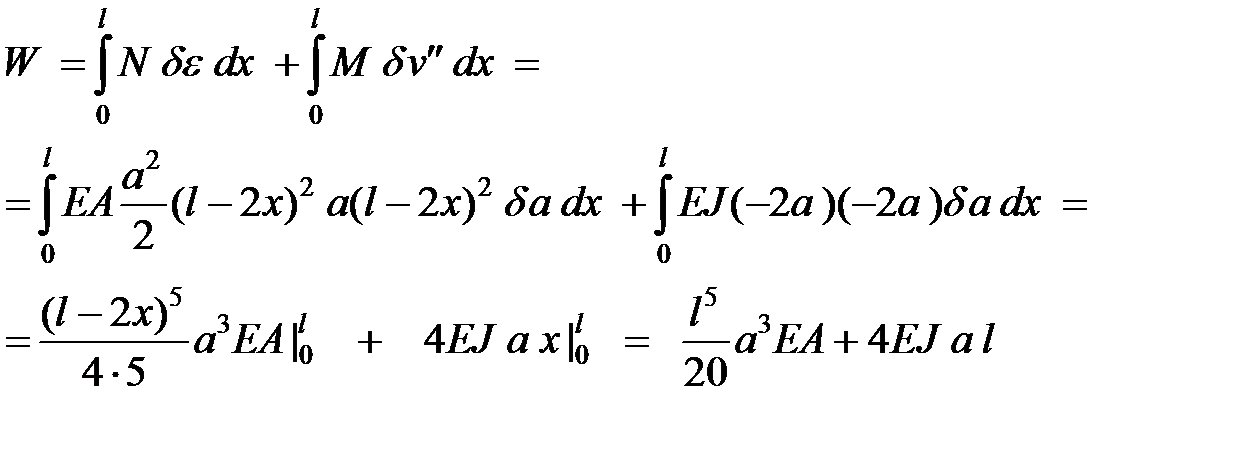
Работа нагрузки будет

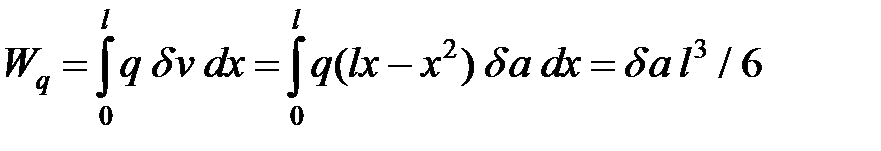
Из условия равенства этих работ получим выражение для нагрузки q, выраженной через параметр a: