Расчет ЖБК по наследственной модели ползучести

F

Решение: Уравнение равновесия:

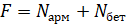
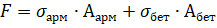
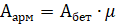
1 уравнение – 2 неизвестных → добавляем геометрическое соображение

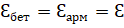
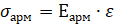
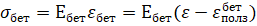(1)

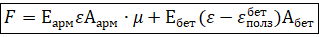(2)

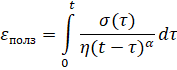
1 шаг: t=0;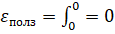

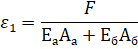
2 шаг: t=t₁; Δt= t₁;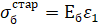

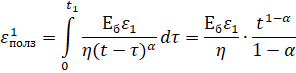
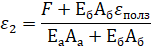
3 шаг: t=t₂=2Δt;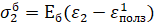

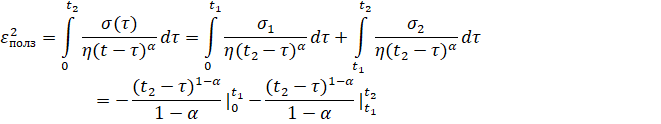
4 шаг: и т.д.

Примечание: видно, что с каждым шагом объем вычислений сильно возрастает.

Заключение по разделу ползучести:

1) Из строительных материалов наиболее простые соотношения применяются для стали (при высоких температурах). Для нее справедлива теория течения .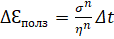

2) Стеклопластик и бетон должны описываться наследственной теорией. Однако в простейших случаях, когда σ=const, можно применить теорию упрочнения .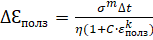

3) В балках-стенках, пластинах и оболочках возникают несколько напряжений 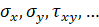и деформаций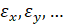

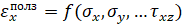
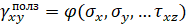
Ясно, что экспериментально найти функци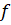и и 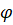без упрощающих предположений - трудновыполнимая задача. Одним из упрощающих гипотез является предположение о том, что от среднего напряжения 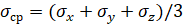ползучесть не зависит.

Ползучесть возникает из-за деформации сдвига, значит, под действием 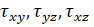. Вместо трех компонентов вводят один параметр, который эквивалентен эти трем. Функци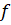и и 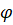становятся одномерными.

Меры деформации

1.В сопромате: линейная деформация 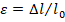- мера деформаций Коши

2.Мера деформаций Грина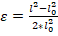

3.Мера деформаций Альманзи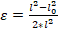

4.Мера деформаций Генки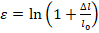

Если 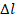мало, то они все с большой точностью совпадают.

Пример: ,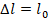

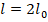
Коши: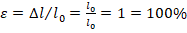

Грина: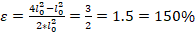

Альманзи: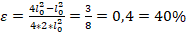

Генки: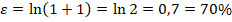

В строительстве 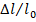очень мало, поэтому можно пользоваться простейшими мерами Коши.

Примечание: Аналогично можно ввести различные меры напряжений.

Например, мера напряжений Коши: 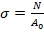- (условное напряжение); мера напряжений Пиолы-Кирхгоффа: .

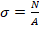Каждой мере деформаций может соответствовать только одна мера напряжений. Выбор осуществляется на основе закона сохранения энергии

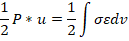
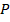
В дальнейшем будем использовать меры Коши для деформаций и напряжений.

Соотношение Коши для малых деформаций при немалых перемещениях.

В линейной теории считается, что премещения и углы поворота малы. Это дает (см. рис):

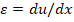
dx

u du

u,v – перемещения по горизонтали и вертикали.

Рассмотрим случай немалых углов поворота.

ds

ds₀

Упрощение: в строительстве в основном используются стержневые и балочные элементы, поэтому рассматривают только изменения продольных элементов (см. рис.), т.е. можно считать, что рассматриваются элементы, направленные вдоль оси х, следовательно, первоначально dy = 0. Тогда

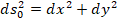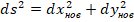, s w:val="24"/><w:lang w:val="EN-US"/></w:rPr><m:t>+</m:t></m:r><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/><w:lang w:val="EN-US"/></w:rPr><m:t>du</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 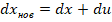; 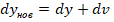dv

Найдем сначала деформацию Грина

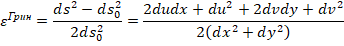
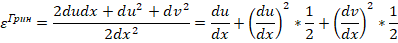
Для дальнейшего упрощения рассуждаем от противного: пусть 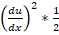не мало, тогда du/dx тоже не мало. Следовательно, 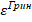- не мало, а поскольку 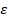мало, то получается противоречие. Следовательно,

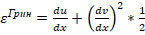
Рассмотрим задачу вычисления малой деформации Коши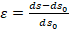

Покажем, что приближенно 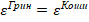. Действительно,

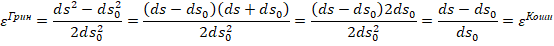
ПРИМЕР 1

Снова рассмотрим изгиб балки под действием продольной центральной силы Р, но предварительно изогнутой в поперечном направлении приложенными по концам сосредоточенными моментами m (см. рис. 17.12). Этот момент может быть вызван внецентренным нагружением продольной силой Р, если он имеет эксцентриситет е. Тогда m=Ре.

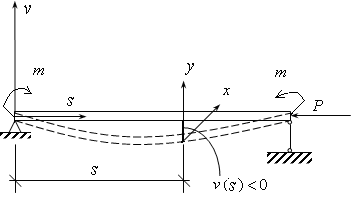
Рис. 17.12

Уравнение изогнутой оси (17.1) примет вид

.

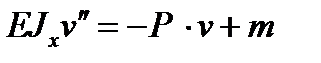Поделив на 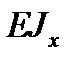и принимая обозначение 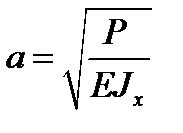, решение этого уравнения запишем в виде суммы однородного и частного решений

.

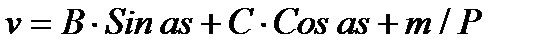Константы В и С отыскиваем из условий закрепления:

(1): 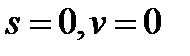на левом краю

(2): 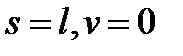на правом краю

Это дает:

(1): 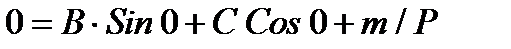на левом краю

(2): 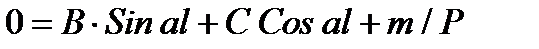на правом краю

Отсюда

(1):

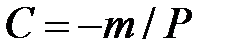
(2):

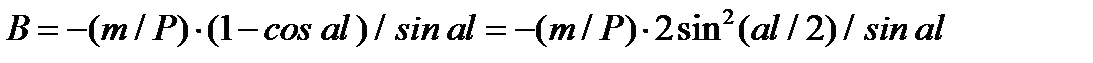
При 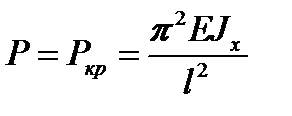, то есть при 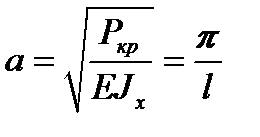, имеем .

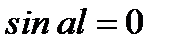Тогда из выражения для В вытекает, что

.

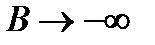Следовательно, при Р→Р_кр получаем неограниченно большие прогибы:

.

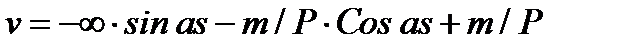Таким образом, при внецентренном сжатии или при наличии поперечных сил балка может получить очень большие прогибы и напряжения даже при малых сжимающих силах, но близких к Р_кр.

ПРИМЕР 2

В качестве второго примера рассмотрим задачу о деформации фермы Мизеса

h

F

a

a0

l0

w

A

b

b

Рис.2.1

Для простоты будем считать 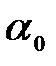малым.

Сжимающие усилия будут

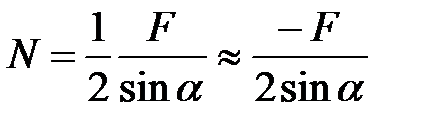(2.1)

Перемещение 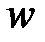вызывает укорочение

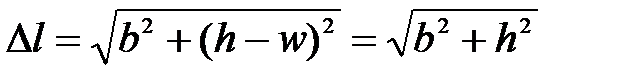(2.2)

Согласно закону Гука

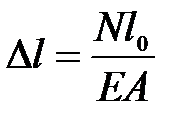(2.3)

Подставляя 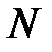, найденное из (2.3) в (2.1) получим

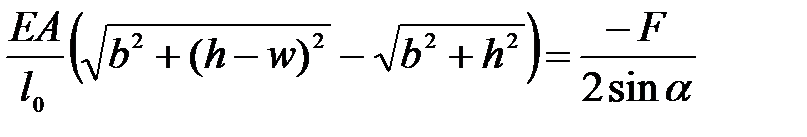(2.4)

Из рисунка 2.1 видно, что

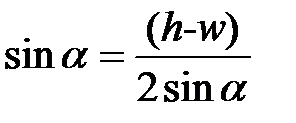(2.5)

Окончательно получаем следующую связь силы 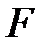с перемещением :

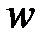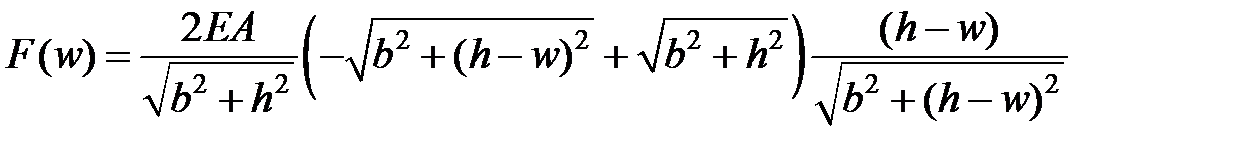(2.6)

Зависимость 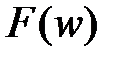имеет вид, представленный на рис.2.2.

w

F

B

h

C

2h

Рис.2.2

Если задавать в качестве параметра процесса нагрузку 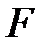, то построение этой кривой вызывает известные трудности. В задачах о больших перемещениях они преодолеваются методами продолжения по различным параметрам (при этом иногда можно использовать методы смены параметра нагружения).

ПРИМЕР 3

Рассмотрим пример применения уточненных выражений для деформаций в задаче об изгибе под равномерной нагрузкой балки с неподвижными шарнирными опорами.

Точное решение.

Рассмотрим сначала решение задачи в точной постановке.

v(x)

q

q

α

α

Q

M

N

R1

Если балка жестко шарнирно закреплена, то видно, что балка удлинится, значит в ней кроме Q и M появится сила растяжения N.

Считаем, что справедлив закон Гука: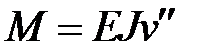

Рассмотрим соотношения теоремы Шведлера-Журавского.

Возьмем сечение правее на Δх, тогда плечо увеличится на Δx. Значит изменение момента будет ΔМ = Q Δx . При бесконечно малых приращениях Δx получим

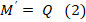
Таким образом, 1-я теорема не изменилась.

Вторая теорема будет модернизирована. На вертикаль кроме R, Q, q проецируется N, поэтому изменение поперечной силы будет

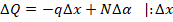
При бесконечно малых приращениях Δx получим

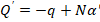
Как известно из математического анализа при малых углах наклона кривой:

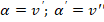v”

Таким образом, получаем уточненное второе соотношение теоремы Шведлера-Журавского

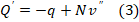(3)

Далее запишем закон Гука при изгибе

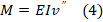
Добавим выражение для продольных деформаций и первое соотношение теоремы Шведлера-Журавского

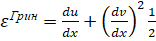(5)

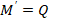(6)

Добавим еще одно уравнение равновесия

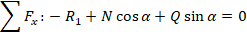
Поскольку в реальных конструкциях α мало, поэтому 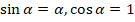, то получим

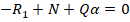
Поскольку α мало, то слагаемым 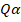можно пренебречь.

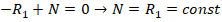
Отсюда вытекает, что приближенно можно считать силу растяжения балки постоянной по ее длине:

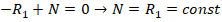(7)

Получили систему уравнений (3)-(7. Её особенность в том, что она нелинейная.

Как обычно в сопромате исключим Q, M из уравнений (3), (4), (6). Тогда получим

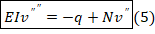(8)

Решение представимо в виде (далее продольная координата х заменена на )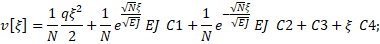

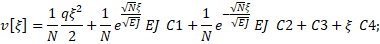(9)

Граничные условия имеют вид

,

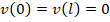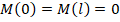
Из этих условий получаем

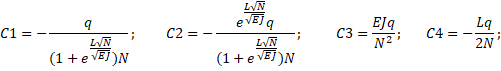
По з. Гука s w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 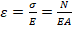. Подставим в ур. (1).

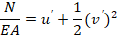
Отсюда

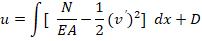
После интегрирования получим

u = D + 1/(24 N^7/2) ((6 EJ^3/2 q²)/(1+ )²-(6 EJ^3/2 q²)/(1+ )²+(12 EJ q² (2 - (L-2 ξ)))/(1+ )-(12 EJ q² (2 + (L-2 ξ)))/(1+ )+(24 N^9/2 ξ)/(AE)+6 L N^3/2 q² ξ²-4 N^3/2 q² ξ³-3 q² ξ (L² N-2 EJ Sech[(L )/(2 )]²))

Константу D найдем из граничного условия:

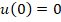
D = (-((6 EJ^3/2 q²)/(1+ )²)+(6 EJ^3/2 q²)/(1+ )²+(12 EJ (2 -L ) q²)/(1+ )-(12 EJ (2 +L ) q²)/(1+ ))/(24 N^7/2);

Второе граничное условие 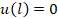дает связь q и N

q = (24 (1+ )² N⁴)/(A E (-24 EJ+L² N+2 L² N+ L² N)); (10)

Для отыскания зависимости усилия растяжения N, прогиба и напряжений используют следующую процедуру:

1) Задают разные значения усилия растяжения N=0; 0.1; 0.2;…

2) Находят q из соотношения (10)

3) Подставляют их в выражение (9) для прогиба и вычисляют момент из закона Гука:

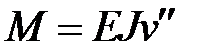
4) После этого находят максимальное напряжение:

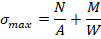
Как видно из решения, процедура расчета прогибов и напряжений достаточно сложная.