Числовые типы, оператор присваивания

2.Поменять местами значение целых переменных х и у, не используя дополнительные переменные.

3.Вычислить значения выражений:

а) not odd (n) при n = 0;

б) t and (p mod 3 = 0) при t = True, p = 101010;

в) (х ´ у <>0) and (у > х) при х = 2, у = 1;

г) (х ´ у <>0) or (у > х) при х = 2, у = 1;

д) a or (not b) при а = False, b = True.

Алгоритмы линейной структуры

Алгоритм линейной структуры ‑ алгоритм, в котором блоки вы­пол­няются последовательно друг за другом, в порядке, заданном схемой. Такой порядок выполнения называется естественным.

5.Вычислить площадь треугольника со сторонами a, b, c по формуле Герона: , где .

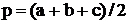6.Вычислить для усеченного конуса площадь поверхности и объем .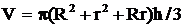

7.Вычислить координаты центра тяжести трех материальных точек с массами и координатами по формулам: ; .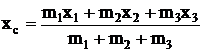

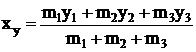8.Вычислить высоты треугольника со сторонами а, b, c, организуя ввод данных из блока данных и вывод результатов с их наименованиями.

Алгоритмы разветвляющей структуры

Часто в зависимости от каких-либо промежуточных результатов вы­чис­ления производятся либо по одним, либо по другим формулам, т.е. в зависимости от выполнения некоторого логического условия вычислительный процесс осуществляется по одной или другой ветви.

Алгоритм такого вычислительного процесса называется алгорит­мом разветвляющей структуры.

7.Вычислить:

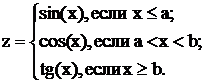
8.Найти квадрат наибольшего из двух чисел a и b и отпечатать

N = 1, если наибольшим является а, и признак N = 2 ‑ в противном случае.

9.Определить, попадает ли точка с координатами х, у в круг радиуса r (уравнение окружности ). Вывести признак N = 1, если точка находится внутри круга, и признак N = 0, если точка находиться вне круга.

10.Составить программу, выполняющую упорядочение трех чисел A, B, C, таким образом, чтобы при выполнении ее в ячейке с симво­лическим адресом A находилось наименьшее число, в ячейке B ‑ сред­нее, в ячейке C ‑ наибольшее.

11.Записать указанное действие в виде одного условного оператора:

а) у =

б) переменной х присвоить корень уравнения .

в) перераспределить значение переменных х и у так, чтобы в х оказалось большее из этих значений, а в у ‑ меньшее;

г) d = max (a, b, c);

д) z =

е) переменной k присвоить номер четверти плоскости, в которой находится точка с координатами х и у (ху 0);

12.Записать программу для решения задачи:

а) по номеру у (у > 0) некоторого года определить с ‑ номер его столетия (учесть, что, к примеру, началом XX столетия был 1901);

б) ;

в) если уравнение ax² + bx +c = 0 (a 0) имеет вещественные корни, то логической переменной t присвоить значение True, а переменным xl и х2 ‑ сами корни, иначе переменной t присвоить False, а значение пере­мен­­ных xl и х2 не менять;

г) считая, что стандартные функции sin и cos применимы только к аргументам из отрезка [0, ], вычислить у = sin х для произвольного числа х;

д) значения переменных а, b и c поменять местами так, чтобы оказалось а b c.