Выбор вида регрессионной модели
Используемый при проведении регрессионного анализа МНК обеспечивает минимизацию отклонений измеренных значений  от предсказанных
от предсказанных  при заданной исследователем структуре модели, что не говорит о том, что модель хорошо описывает изучаемый процесс. При выборе вида модели необходимо уделить внимание следующим положениям:
при заданной исследователем структуре модели, что не говорит о том, что модель хорошо описывает изучаемый процесс. При выборе вида модели необходимо уделить внимание следующим положениям:
- Наличие имеющихся знаний при построении моделей, описывающих процессы, подобные моделируемому текущему процессу. Важно знать какими моделями описывали исследователи подобные процессы и как они себя проявили.
- Выбор модели, отражающей реальные закономерности, наблюдаемые в процессе.
- Стремиться применять простые виды функциональных зависимостей, близко расположенных к выборке данных.
- В случае нелинейного вида модели, желательно отдавать предпочтение нелинейным моделям, которые можно преобразовать к псевдолинейному виду посредством ввода новых регрессоров  . Например, допустим выбрана модель вида
. Например, допустим выбрана модель вида  , тогда вводя новые переменные
, тогда вводя новые переменные  , получим псевдолинейную модель вида
, получим псевдолинейную модель вида  . Таким образом, определив значения псевдолинейной модели
. Таким образом, определив значения псевдолинейной модели  легко восстановить значения исходной нелинейной модели
легко восстановить значения исходной нелинейной модели  . Пример нелинейной модели
. Пример нелинейной модели  , которую нельзя свести к виду псевдолинейной модели.
, которую нельзя свести к виду псевдолинейной модели.
- Если речь идет о парной регрессии, то можно провести анализ расположения точек на графике, посредством которого провести выбор модели. На рис. 1 представлен пример подбора вида полинома для отклика  как функции одного фактора
как функции одного фактора 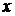 (эмпирические данные на графике представлены в форме звездочек). Из рисунка видно, что точность линейной модели
(эмпирические данные на графике представлены в форме звездочек). Из рисунка видно, что точность линейной модели  будет неудовлетворительной в силу большого значения остаточной суммы квадратов ошибки. В данной ситуации приемлемо использование полинома третьей степени
будет неудовлетворительной в силу большого значения остаточной суммы квадратов ошибки. В данной ситуации приемлемо использование полинома третьей степени  . Однако возможен поиск и других видов регрессионных моделей, дающих более точный прогноз.
. Однако возможен поиск и других видов регрессионных моделей, дающих более точный прогноз.

Рис. 1. Графики парной регрессии
Если указанные положения невозможно оценить, а исследователь приступает к изучению процесса, о котором не имеет ясного представления и не может сориентироваться при выборе структуры модели, можно воспользоваться одним из подходов:
1. В том случае, когда из описания исследуемого процесса следует, что он представляет собой непрерывную функцию факторов, отражающую отклик процесса, то обычно используют полиномиальную модель (4). При этом необходимо определиться с максимально возможной степенью полинома. При построении регрессионной модели с учетом  факторов
факторов  и предположением того, что к изучаемому процессу можно применить полином не выше второй степени, с учетом (4) можно записать новый полином как:
и предположением того, что к изучаемому процессу можно применить полином не выше второй степени, с учетом (4) можно записать новый полином как:

Сформированная подобным образом структура учитывает все возможные комбинации регрессоров модели. Дальнейший анализ модели позволит выявить незначимые оценки коэффициентов  , что в результате приведет к удалению из модели соответствующих регрессоров и как результат приведет к ее постепенному упрощению.
, что в результате приведет к удалению из модели соответствующих регрессоров и как результат приведет к ее постепенному упрощению.
2. Проверка всех возможных регрессий. Суть заключается в вычислении коэффициентов для всех возможных регрессионных моделей с дальнейшим сравнением их качественных характеристик. Если модель содержит  коэффициентов, то:
коэффициентов, то:
- Все модели делятся на  подмножеств. Первое подмножество включает модель
подмножеств. Первое подмножество включает модель  , второе подмножество включает все модели с двумя коэффициентами и так далее.
, второе подмножество включает все модели с двумя коэффициентами и так далее.
- В каждом подмножестве модели упорядочиваются по возрастанию коэффициента множественной корреляции 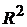 .
.
- В каждом подмножестве исследуется одно уравнение с максимальным значением 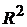 . Если при переходе от модели одного подмножества к модели другого подмножества не наблюдается существенного увеличения
. Если при переходе от модели одного подмножества к модели другого подмножества не наблюдается существенного увеличения 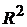 , то оставляют модель с меньшим числом регрессоров.
, то оставляют модель с меньшим числом регрессоров.
Данный подход наиболее точный, но и самый трудоемкий.
3. Метод включения. Исследование начинается с модели  . Затем поочередно один за другим добавляются новые регрессоры. Порядок включения регрессоров определяется частным коэффициентом корреляции регрессоров с откликом. Включаемый на данном этапе регрессор должен иметь максимальный частный коэффициент корреляции. С введением нового регрессора проводится качественная оценка модели. Добавление новых регрессоров продолжается до тех пор, пока величина частного критерия
. Затем поочередно один за другим добавляются новые регрессоры. Порядок включения регрессоров определяется частным коэффициентом корреляции регрессоров с откликом. Включаемый на данном этапе регрессор должен иметь максимальный частный коэффициент корреляции. С введением нового регрессора проводится качественная оценка модели. Добавление новых регрессоров продолжается до тех пор, пока величина частного критерия 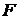 не станет меньше значения распределения Фишера
не станет меньше значения распределения Фишера  .
.
Существуют и другие подходы выбора структуры регрессионной модели.
