Нормальное распределение НСВ

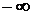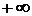Случайная величина Х, принимающая любые значения от до , имеет нормальное распределение с параметрам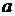и и 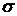, если ее плотность распределения имеет вид:

.

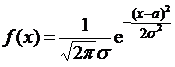Нормальный закон распределения (также часто называемый законом Гаусса) имеет исключительное значение в теории вероятностей, т. к. это – наиболее часто встречающийся на практике закон распределения. Нормальное или близкое к нему распределение имеет огромное число случайных величин, встречающихся нам в жизни. Общим для их поведения является следующее: наиболее часто встречаются (наиболее вероятны) значения случайной величины, близкие к ее среднему арифметическому значению 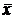. Чем сильнее отличаются значения от 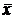(неважно, в большую или меньшую сторону), тем реже они встречаются (тем менее вероятны).

На рисунке слева приведен вид графиков 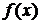при различных значениях :

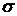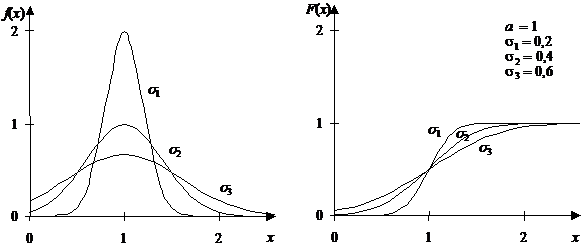
Характерная колоколообразная кривая, изображенная на рисунках, имеет специальное название — гауссиан (гауссова кривая).

Параметр 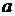представляет собой математическое ожидание (а также моду и медиану) величины, распределенной по нормальному закону, а параметр 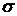– среднеквадратическое отклонение этой величины. Функция распределения в нормальном законе

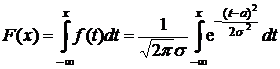
не имеет аналитического выражения и вычисляется с помощью таблиц вспомогательной функции Ф( ). (Вид графика этой функции приведен выше на рисунке справа). Эта функция имеет различные названия: интеграл (функция) Лапласа, интеграл вероятностей, функция ошибок, функция распределения (нормированного) нормального распределения. Эта функция может не только по-разному называться, но и приводиться в несколько различном виде, что следует учитывать, пользуясь ею.

Рассмотрим наиболее часто встречающуюся задачу: расчет вероятности попадания значений Х в заданный интервал :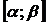

.

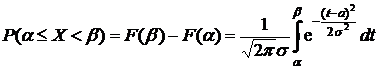1) Если ,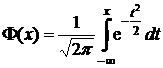

то .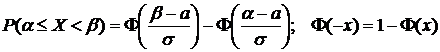

2) Если ,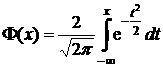

то .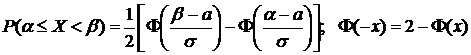

3) Если ,

то .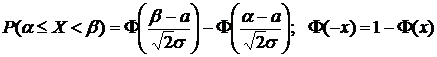

4) Если ,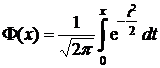

то .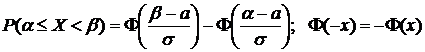

5) Если ,

то .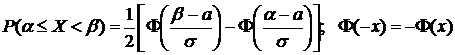

6) Если ,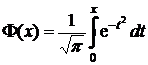

то .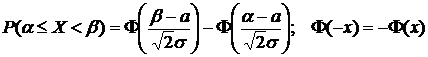

Пользуясь любым видом функции Ф( ) можно подсчитать, что

.

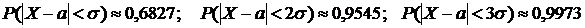Таким образом, практически достоверным событием (вероятность которого близка к 1) является попадание значений нормально распределенной величины на конечный промежуток от 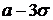до 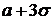. Это обстоятельство позволяет успешно применять нормальный закон для описания поведения многих случайных величин, встречающихся в опыте, значения которых, конечно, меняются не от – 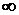до + 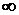, а на каком-либо конечном промежутке.

Кроме задачи вычисления вероятности попадания значений функции на интервал, встречается и обратная задача: по заданной вероятности установить интервал, симметричный относительно М(Х), на котором могут находиться значения случайной величины. Обычно задаваемую вероятность называют доверительной, обозначают 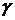, а интервал, в котором с вероятностью 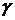находятся значения случайной величины – доверительным.

Пусть .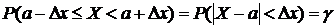

Используя , получим 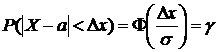, откуда найдем, что .

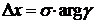В таблице приведены значения 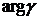при различных .

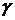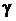	0,99	0,95	0,9	0,8	0,7	0,6	0,5
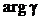	2,58	1,96	1,64	1,28	1,04	0,84	0,67