IV. Разложение элементарных функций в ряд Маклорена.

Для приложений важно уметь данную функцию 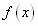разлагать в степенной ряд, т.е. функцию 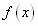представлять в виде суммы степенного ряда.

Рядом Тейлора для функции 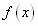называется степенной ряд вида

.

Если , то получим частный случай ряда Тейлора

,

который называется рядом Маклорена.

Степенной ряд внутри его промежутка сходимости можно почленно дифференцировать и интегрировать сколько угодно раз, причем полученные ряды имеют тот же промежуток сходимости, что и исходный ряд.

Два степенных ряда можно почленно складывать и умножать по правилам сложения и умножения многочленов. При этом промежуток сходимости полученного нового ряда совпадает с общей частью промежутков сходимости исходных рядов.

Для разложения функции 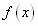в ряд Маклорена необходимо:

Вычислить значения функции и ее последовательных производных в точке 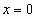, т.е. , , ,…, ;

Составить ряд Маклорена, подставив значения функции и ее последовательных производных в формулу ряда Маклорена;

Найти промежуток сходимости полученного ряда по формуле

, .

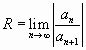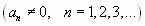Таблица, содержащая разложения в ряд Маклорена некоторых элементных функций:

.

.

.

.

.

.

Пример 1. Разложить в ряд Маклорена функцию .

Решение. Так как , то, заменяя 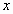на в разложении , получим:

, .

Пример 2. Выписать ряд Маклорена функции .

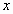Решение. Так как , то воспользовавшись формулой , в которой заменим на , получим:

,

или

,

если

, т.е. .

Пример 3. Разложить в ряд Маклорена функцию .

Решение. Воспользуемся формулой . Так как

, то заменив 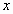на получим:

, или

,

где , т.е. .

V. Практические задания для самоконтроля студентов.

При помощи признака сравнения рядов установить сходимость

или расходимость рядов:

.

.

.

.

.

Исследовать по признаку Даламбера сходимость рядов:

.

.

.

.

.

Исследовать на сходимость (абсолютную или условную) знакочередующийся ряд:

.;

.;

.;

.;

.

Найти промежутки сходимости нижеследующих рядов и выяснить вопрос об их сходимости на концах промежутков сходимости:

;

;

;

;

.

Используя разложения в ряд Маклорена функции , , , , разложить степенные ряды функции:

.

.

.

.

.

VI. Ответы

I.

1. сходится;
2. расходится;
3. сходится;
4. сходится;
5. расходится;
6. сходится;
7. сходится;
8. расходится;
9. сходится;
10. сходится.

II.

1. cходится абсолютно;
2. cходится абсолютно;
3. cходится условно;
4. cходится условно;
5. cходится абсолютно.

III.

1. ;
2. ;
3. ;
4. ;
5. .

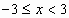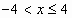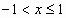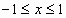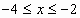IV.

;

;

;

;

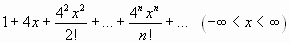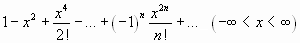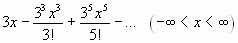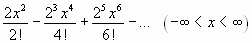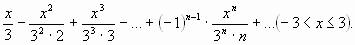
VII. Историческая справка.

Решение многих задач сводится к вычислению значений функций и интегралов или к решению дифференциальных уравнений, содержащих производные или дифференциалы неизвестных функций.

Однако точное выполнение указанных математических операций во многих случаях оказывается весьма затруднительным или невозможным. В этих случаях можно получить приближенное решение многих задач с любой желаемой точностью при помощи рядов.

Ряды представляют собой простой и совершенный инструмент математического анализа для приближенного вычисления функций, интегралов и решений дифференциальных уравнений.

Теория рядов создавалась в тесной связи с теорией приближенного представления функций в виде многочленов. Впервые это сделал И. Ньютон (1642 – 1727). в 1676г. В его письме к секретарю Лондонского Королевского Общества появилась формула:

,

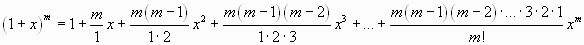которую мы знаем как формулу бинома Ньютона.

Здесь мы видим функцию 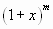, представленную в виде многочлена. Но если число 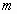не является натуральным, в правой части равенства получается не полином, а бесконечная сумма слагаемых, то есть ряд.

Развивая идею Ньютона, английский математик Брук Тейлор (1685 – 1731) в 1715г. доказал, что любой функции, имеющей в точке 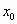производные всех порядков, можно сопоставить ряд:

.

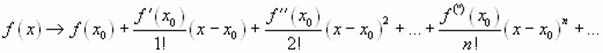Мы не можем пока поставить знак равенства между функцией 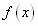, принимающей конечное значение для любого значения 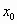, и стоящим справа функциональным рядом.

Для того, чтобы вместо знака “ 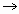” можно было поставить знак равенства, необходимо провести некоторые дополнительные рассуждения, связанные именно с бесконечностью числа слагаемых в правой части равенства и касающиеся области сходимости ряда.

При 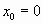формула Тейлора принимает вид, в котором называется формулой Маклорена:

.

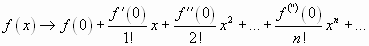Колин Маклорен (1698 – 1746), ученик Ньютона, в работе “Трактат о флюксиях” (1742) установил, что степенной ряд, выражающий аналитическую функцию, - единственный, и это будет ряд Тейлора, порожденный такой функцией. В формуле бинома Ньютона коэффициенты при степенях 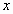представляют собой значения 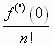, где .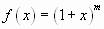

Итак, ряды возникли в XVIII в. как способ представления функций, допускающих бесконечное дифференцирование. Однако функция, представляемая рядом, не называлась его суммой, и вообще в то время не было еще определено, что такое сумма числового или функционального ряда, были только попытки ввести это понятие.

Например, Л. Эйлер (1707-1783), выписав для функции соответствующий ей степенной ряд, придавал переменной 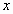конкретное значение 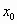. Получался числовой ряд. Суммой этого ряда Эйлер cчитал значение исходной функции в точке 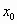. Но это не всегда верно.

О том, что расходящийся ряд не имеет суммы, ученые стали догадываться только в XIX в., хотя в XVIII в. многие, и прежде всего Л. Эйлер, много работали над понятиями сходимости и расходимости. Эйлер называл ряд 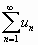сходящимся, если его общий член 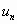стремится к нулю при возрастании .

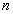В теории расходящихся рядов Эйлер получил немало существенных результатов, однако результаты эти долго не находили применения. Еще в 1826г. Н.Г. Абель (1802 – 1829) называл расходящиеся ряды “дьявольским измышлением”. Результаты Эйлера нашли обоснование лишь в конце XIX в.

В формировании понятия суммы сходящегося ряда большую роль сыграл французский ученый О.Л. Коши (1789 – 1857); он сделал чрезвычайно много не только в теории рядов, но и теории пределов, в разработке самого понятия предела. В 1826г. Коши заявил, что расходящийся ряд не имеет суммы.

В 1768г. французский математик и философ Ж.Л. Д’Аламбер исследовал отношение последующего члена к предыдущему в биномиальном ряде и показал, что если это отношение по модулю меньше единицы, то ряд сходится. Коши в 1821г. доказал теорему, излагающую в общем виде признак сходимости знакоположительных рядов, называемых теперь признаком Д’Аламбера.

Для исследования сходимости знакочередующихся рядов используется признак Лейбница.

Г.В. Лейбниц (1646 – 1716), великий немецкий математик и философ, наряду с И. Ньютоном является основоположником дифференциального и интегрального исчисления.

Список литературы:

Основная:

1. Богомолов Н.В., Практические занятия по математике. М., “Высшая школа”, 1990 – 495 с.;
2. Тарасов Н.П., Курс высшей математики для техникумов. М., “Наука”, 1971 – 448 с.;
3. Зайцев И.Л., Курс высшей математики для техникумов. М., государственное издательство техникумов – теоретической литературы, 1957 - 339 с.;
4. Письменный Д.Т., Курс лекций по высшей математике. М., “Айрис Пресс”, 2005, часть 2 – 256 с.;
5. Выгодский М.Я., Справочник по высшей математике. М., “Наука”, 1975 – 872 с.;