ОПРЕДЕЛЕНИЕ: Две матрицы называются эквивалентными, если они имеют один и тот же ранг.
ТЕОРЕМА 2:Какую-либо ненулевую матрицу с помощью элементарных преобразований можно привести к матрице ступенчатого вида.
Матрица А называется ступенчатой, если она имеет вид:
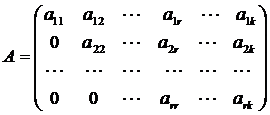 , где
, где 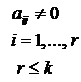
Замечания: 1. Условие 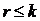 , т.е., количество строк не больше количества столбцов, всегда может быть достигнуто транспонированием матрицы.
, т.е., количество строк не больше количества столбцов, всегда может быть достигнуто транспонированием матрицы.
2. Если в ступенчатой матрице количество строк равно количеству столбцов, то такую матрицу называют треугольной.
Очевидно, что ранг ступенчатой матрицы равен 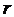 , т.к. имеется минор
, т.к. имеется минор 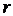 -го порядка, не равный нулю:
-го порядка, не равный нулю:
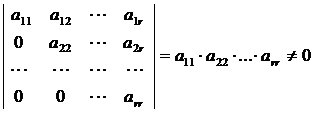 .
.
Таким образом, с помощью элементарных преобразований матрицу можно привести к так называемому ступенчатому виду, когда вычисление ее ранга несложно, т.к., для этого достаточно посчитать количество строк матрицы ступенчатого вида.
Пример: Вычислить ранг матрицы с помощью элементарных преобразований (выбранные строки или столбцы нумеруем с помощью римских цифр, выполняемые преобразования записываем напротив выбранных строк или столбцов)
Решение: Выполняем элементарные преобразования
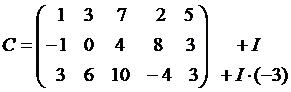
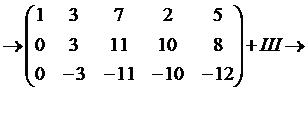
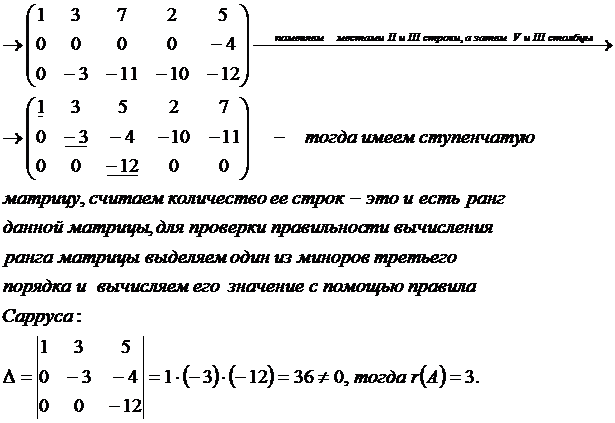

УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Проверить, что ранги указанных матриц равны 2, 3, 2, 1
соответственно: 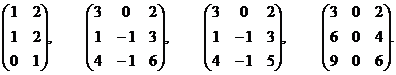
2. С помощью элементарных преобразований вычислить ранг указанных матриц:
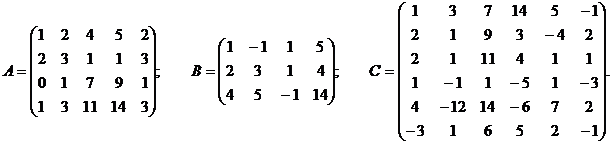
IV. «ОБРАТНАЯ МАТРИЦА».
Определение: Матрица 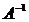 называется обратной по отношению к квадратной матрице
называется обратной по отношению к квадратной матрице 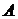 , если при умножении матрицы
, если при умножении матрицы 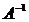 на матрицу
на матрицу 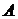 как справа, так и слева, получается единичная матрица:
как справа, так и слева, получается единичная матрица: 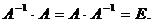
Замечание: Только квадратная матрица имеет обратную. Матрица, обратная данной, тоже квадратная.
Определения: 1. Если определитель матрицы 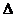 ≠ 0, то матрица называется невырожденной или неособенной.
≠ 0, то матрица называется невырожденной или неособенной.
Если определитель матрицы 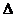 =0, то матрица называется вырожденной или особенной.
=0, то матрица называется вырожденной или особенной.
2. Присоединенная матрица 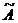 , получается из матрицы
, получается из матрицы 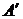 , транспонированной по отношению к матрице
, транспонированной по отношению к матрице 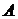 , заменой элементов матрицы
, заменой элементов матрицы 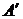 на их алгебраические дополнения.
на их алгебраические дополнения.
Теорема (необходимое и достаточное условие существования обратной матрицы):
Обратная матрица 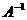 существует и единственна тогда и только тогда, когда матрица
существует и единственна тогда и только тогда, когда матрица  невырожденная, т.е.
невырожденная, т.е. 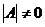 . Ее элементы вычисляются по формуле:
. Ее элементы вычисляются по формуле: 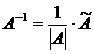 .
.
Алгоритм построения обратной матрицы 1. Вычислим определитель данной матрицы 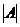 . Если . Если 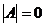 , то для данной матрицы не существует обратной. 2. Если , то для данной матрицы не существует обратной. 2. Если 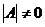 , строим матрицу , строим матрицу 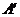 , транспонированную по отношению к матрице , транспонированную по отношению к матрице  , заменяя строки матрицы А ее столбцами. 3. Строим присоединенную матрицу , заменяя строки матрицы А ее столбцами. 3. Строим присоединенную матрицу 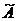 , заменяя элементы матрицы , заменяя элементы матрицы 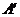 их алгебраическими дополнениями по формуле их алгебраическими дополнениями по формуле 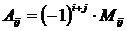 4. Вычисляем обратную матрицу по формуле 4. Вычисляем обратную матрицу по формуле 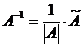 5. При необходимости проверяем правильность вычисления обратной матрицы 5. При необходимости проверяем правильность вычисления обратной матрицы 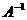 , исходя из ее определения , исходя из ее определения 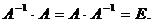 . . |
Пример: 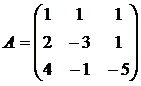 . Найти . Найти 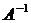 . . |
1. 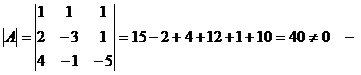 данная матрица имеет обратную. данная матрица имеет обратную. |
2. 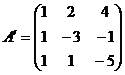 . . |
3. 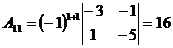 ; ; 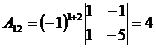 ; ; 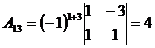 ; ; 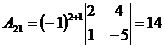 ; ; 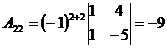 ; ; 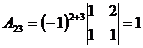 ; ; 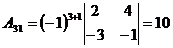 ; ; 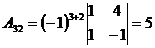 ; ; 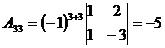 . Получили присоединенную матрицу: . Получили присоединенную матрицу: 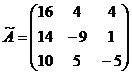 . . |
4. 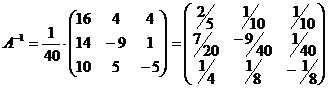 . . |
УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Найти матрицу, обратную данной:
1) 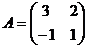 ; 3)
; 3) 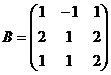 ; 5)
; 5) 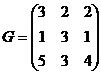 ;
;
2) 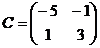 ; 4)
; 4) 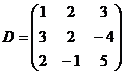 ; 6)
; 6) 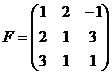 .
.
Проверить для матриц B и D правильность нахождения обратной матрицы (должны быть верными равенства: 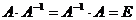 ).
).
