Уравнения, связанные с тригонометрическими уравнениями.
а)½х + 5½ sin x = x + 5.
Уравнение равносильно совокупности 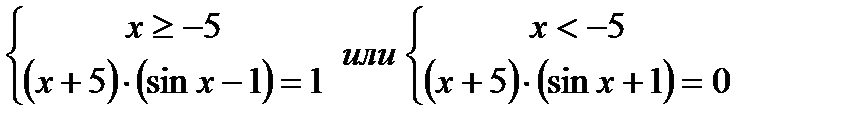
Решением первой системы являетсях = -5, а также корни уравненияsin x = 1, x=p/2 +2pk, kÎZ, удовлетворяющие условиюx³ -5,т.е. p/2 + 2pk³ - 5, полагая-5 » 5/3 p,имеемp/2 + 2pк³- 5 p/3,2pк ³-5p/3 -p/2,к ³ -13/12, k Î Z.к = -1, 0, 1, … .
Решением второй системы являютсякорни уравнения sin x = -1; x= - p/2 + 2pm, mÎZ,
удовлетворяющие условиюх< -5, т.е. - p/2 + 2pm < -5, полагая-5 » -5/3p,имеем
- p/2+2pm < -5p/3,m < - 7/12, mÎZ.m= -1 ,-2, -3,… .
Ответ:-5; p/2+ 2pк(к=-1, 0, 1 ,…);-p/2+2pm (p=-1, -2, -3,…).
б) 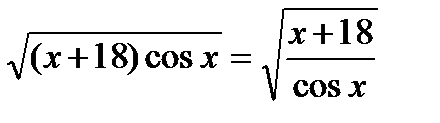
О Д З:(x + 18)cos x³0;cosx ¹ 0
Возведем обе части уравнения в квадрат: 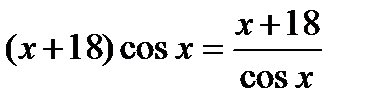 ,
, 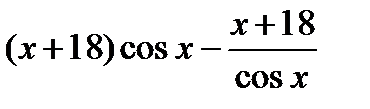 =0
=0
Решим данное уравнениеcos2x(x + 18) - (x + 18) = 0,(cos2x - 1) (x + 18) = 0,
cosx = 1,cosx= - 1,илиx = - 18.
x = 2pk,k Î Zx = p + 2pm,m Î Z
Произведемотбор корнейв соответствии с ОДЗ.
1)х = -18,(18 + 18)cos 18³ 0,cos 18 ³ 0(заметим, что угол, выраженный в радианах, принадлежит четвертой четверти, 18 » 5,7p).cos 18 ³ 0 - верно.
2)х = 2pк,(2pk + 18) cos2pk³ 0,т.к. cos 2pk = 1, тоpk³18
2pk³ - 5,7 p,k³ - 2,85; k =-2,-1, 0, 1,… .
3)х=p + 2pm, (p+ 2pm+ 18)cos (p + 2pm) ³0,т.к.cos (p + 2pm) = -1, то
p +2pm + 18£0,p +2pm £- 18,2pm£ - 5,7 p - p,m£ -3,35; m=-4, -5 , -6,…
Ответ:- 18, 2pк,к=-2, -1, 0, 1 ,…;p+2pm, m = -4, -5, -6, -7,… .
1)½х+3½ sin x=х + 3.Ответ: -3, p/2 + 2pк(к=0, 1, 2, …),
-p/2 + 2pm(m=-1, -2, -3,…)
2)2½x-6½cos x= x - 6.Ответ:6, 4p/3, 7p/3,p/3 + 2pк( к=2, 3, 4,…),
2p/3 + 2pm (m =0, -1, -2, …).
Нестандартныеприёмырешениятригонометрическихуравнений.
а)sin2пх + sin2пy = 0
Суммадвухнеотрицательныхчисел= 0толькотогда, когдакаждоеслагаемое=0
sin2пх =0иsin2пy = 0; пх = пкипy = пс, Ответ:x = к;у = с, гдек, с 
б)1)sinxcos2x = 1/4
Умножим левую и правую часть на cosx  0 ( Проверить, нет ли потери корней)
0 ( Проверить, нет ли потери корней)
sin4x = cosx;sin4x – sin(п/2 – х) = 0; 2sin(5/2 x – п/4) cos(3/2 х + п/4) = 0
Ответ: x = п/10 + 2пk/5 ; x = п/6 + 2пk/3 ,k 
2)8cosx cos2x cos4x = 1* sinx  0
0
sin8x = sinx;sin8x – sinx = 0; 2sin7/2 xcos9/2 x = 0
Ответ: x = 2пk/7 ; x = п/9 + 2пk/9 ; x  пk ,k
пk ,k 
Уравнения, решаемые на основе условия равенства одноимённых функций.
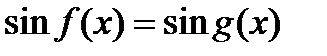 | 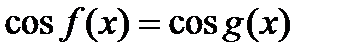 | 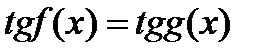 |
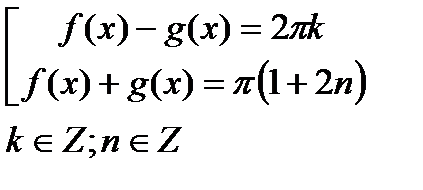 | 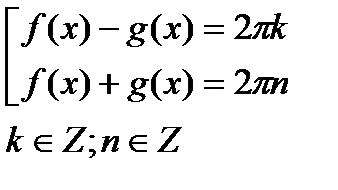 | 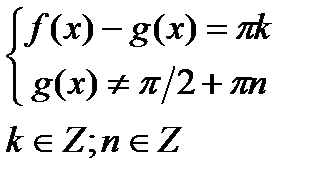 |
1)sin3,8  =sin1,2 =sin1,2  ,т.к. 3,8 ,т.к. 3,8  +1,2 +1,2  =5 =5  2) sin5,3 2) sin5,3  =-sin2,7 =-sin2,7  ,т.к. 5,3 ,т.к. 5,3  -(-2,7 -(-2,7  )=8 )=8  3) sin 3) sin 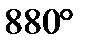 =sin =sin 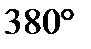 , т.к. , т.к. 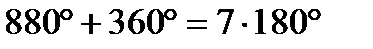 4)sin3,2 4)sin3,2 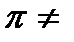 sin0,8 sin0,8  , т.к.не выполнены оба условия , т.к.не выполнены оба условия | 1)сos4,7  =cos3,3 =cos3,3  ,т.к. 4,7 ,т.к. 4,7  +3,3 +3,3  =8 =8  2) cos15 2) cos15  =cos11 =cos11  ,т.к. 15 ,т.к. 15  -11 -11  =4 =4  3) cos17,3 3) cos17,3  =cos11,3 =cos11,3  ,т.к17,3 ,т.к17,3  -11,3 -11,3  =6 =6  4)cos5,3 4)cos5,3 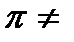 cos3,7 cos3,7  , т.к. не выполнены оба условия , т.к. не выполнены оба условия | 1)tg9,7  =tg1,7 =tg1,7  , т.к.9,7 , т.к.9,7  -1,7 -1,7  =8 =8  2) tg8,7 2) tg8,7  =-tg1,3 =-tg1,3  , т.к. 8,7 , т.к. 8,7  -(-1,3 -(-1,3  )=10 )=10  3) tg1,5 3) tg1,5 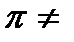 tg2,5 tg2,5  , т.к. тангенсы не существуют 4)tg4,3 , т.к. тангенсы не существуют 4)tg4,3 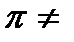 tg(-2,5 tg(-2,5  ), т.к. не выполнены оба условия ), т.к. не выполнены оба условия |
а)sin3x= sin5x
1)5x - 3x = 2  k; x =
k; x =  kили2) 5x + 3x = (2к+1)
kили2) 5x + 3x = (2к+1)  ; x =
; x = 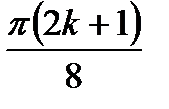 Отв: пk;
Отв: пk; 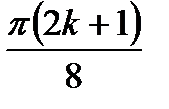 ,k
,k 
б)sinx = cos3x;cos(  /2 – x) = cos3x
/2 – x) = cos3x
1)3x – (  /2 – x) = 2
/2 – x) = 2  k; x =
k; x = 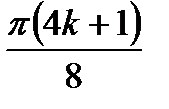 или2) 3x +
или2) 3x +  /2 - x = 2
/2 - x = 2  к; x =
к; x = 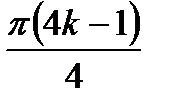
Ответ:x = 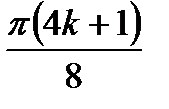 ; x =
; x = 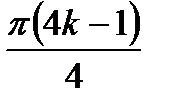 ,k
,k 
в)tg3xtg(5x +  /3) = 1
/3) = 1
Делим обе части уравнения на tg3x. Это возможно, т.к. tg3x  0 по проверке
0 по проверке
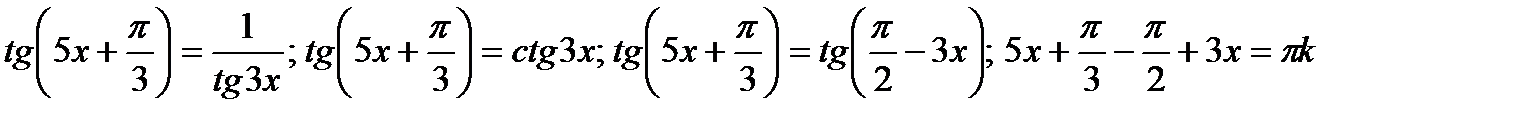
Каждая часть уравнения существует.x = 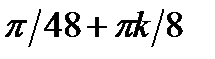 ,k
,k 
Ответ:x = 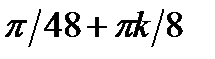 ,k
,k 
Уравнения с обратными тригонометрическими функциями.
Определение: функции f и gназываются взаимно-обратными, если 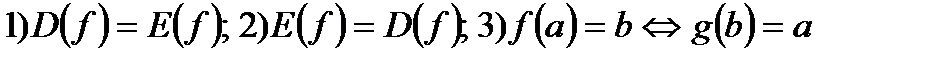
Признак: функция обратима, если разным значениям аргумента соответствуютразные значения функции.Следствие: любая строго-монотонная функция обратима.
Свойства взаимно-обратных функций: свойства 1-3 см.определение; 4)обратная  -
-  ;
;
обратная  -
-  ; 5)обратная нечётной – нечётная; чётная функция обратной не имеет, кроме точечных
; 5)обратная нечётной – нечётная; чётная функция обратной не имеет, кроме точечных 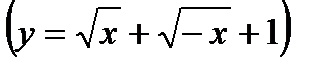 ; 6)графики взаимно-обратных функций симметричны относительно прямой у = х.(Чтобы задать формулой обратную функцию, достаточно решить уравнение относительно хи поменять обозначения
; 6)графики взаимно-обратных функций симметричны относительно прямой у = х.(Чтобы задать формулой обратную функцию, достаточно решить уравнение относительно хи поменять обозначения 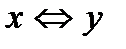 )
)
Обратные тригонометрические функции
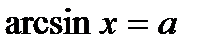 | 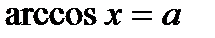 | 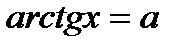 | 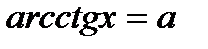 | ||
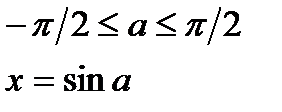 | 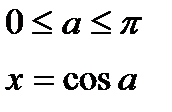 | 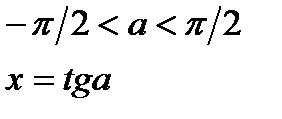 | 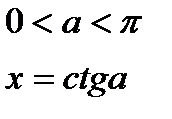 | ||
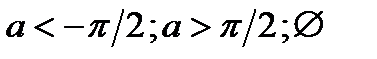 | 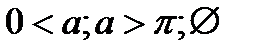 | 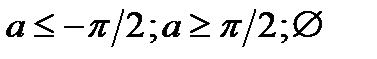 |  | ||
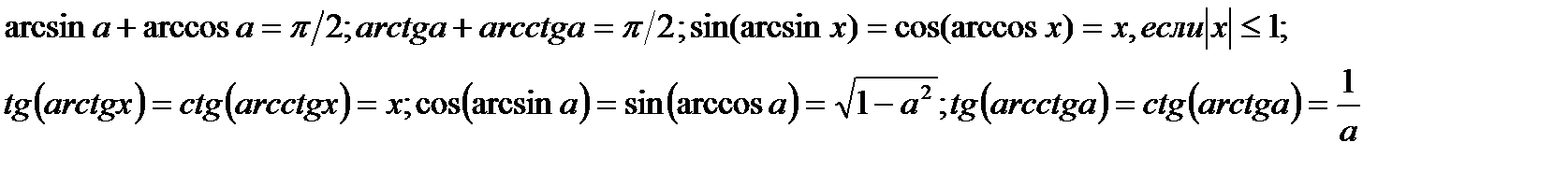 | |||||
| Графики функции | Свойства функций | Примеры | |||
 | y=sinx 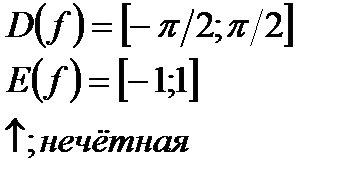 y=arcsinx y=arcsinx 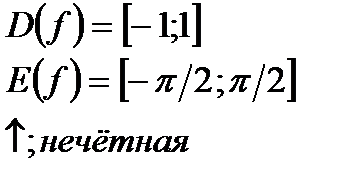 | 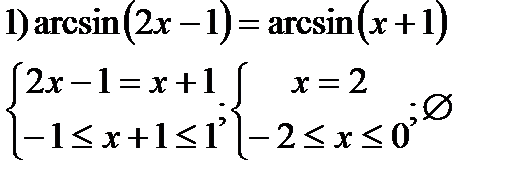 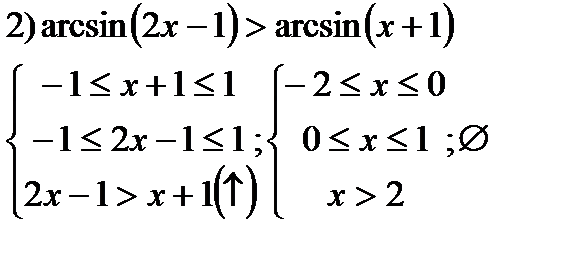 | |||
 | y=cosx 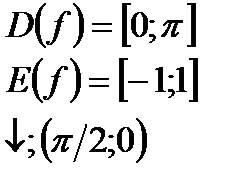 y=arccosx y=arccosx 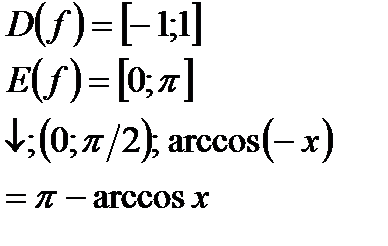 | 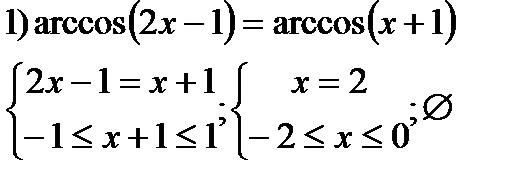 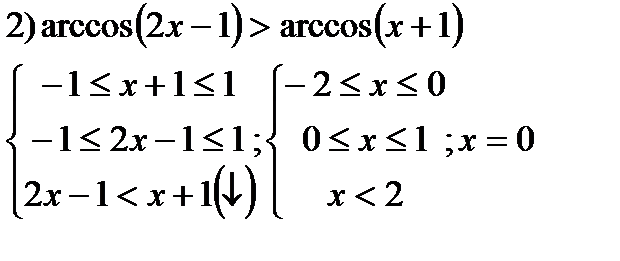 | |||
 | y=tgx 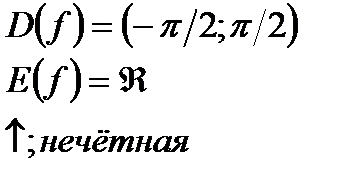 y=arctgx y=arctgx 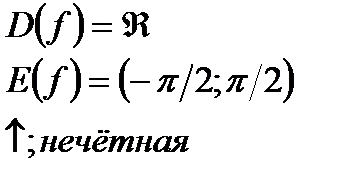 | 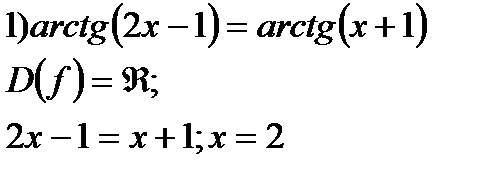 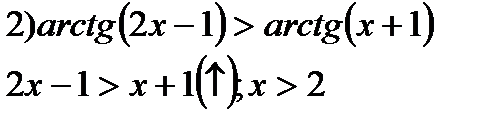 | |||
 | y=ctgx 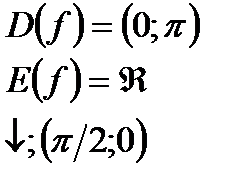 y=arcctgx y=arcctgx 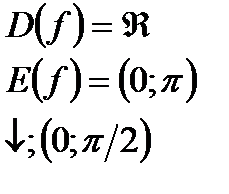 | 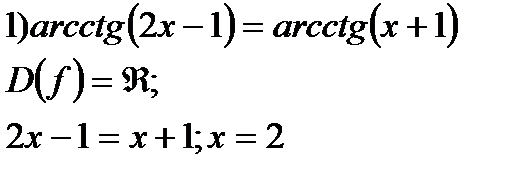 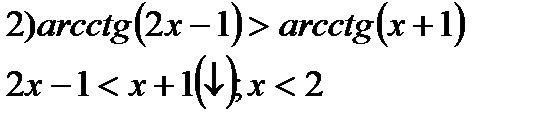 | |||
Уравнения, решаемые по определению.
а)arcsin(sinx)= x – 2п
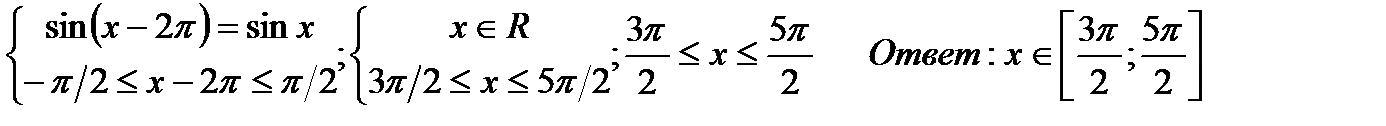
б)arcсos(cosx)= x – 3п/2
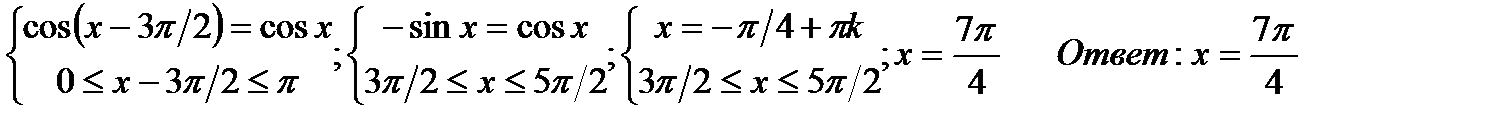
в)arctg 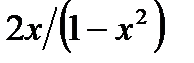 = 2arctgx
= 2arctgx
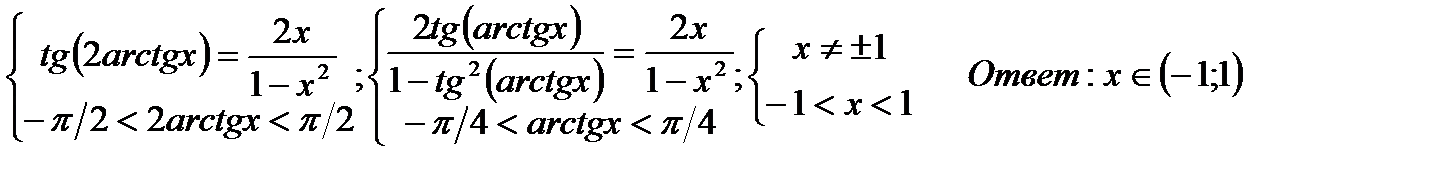
г)arcсos(0,75 - x)=2arcsinx
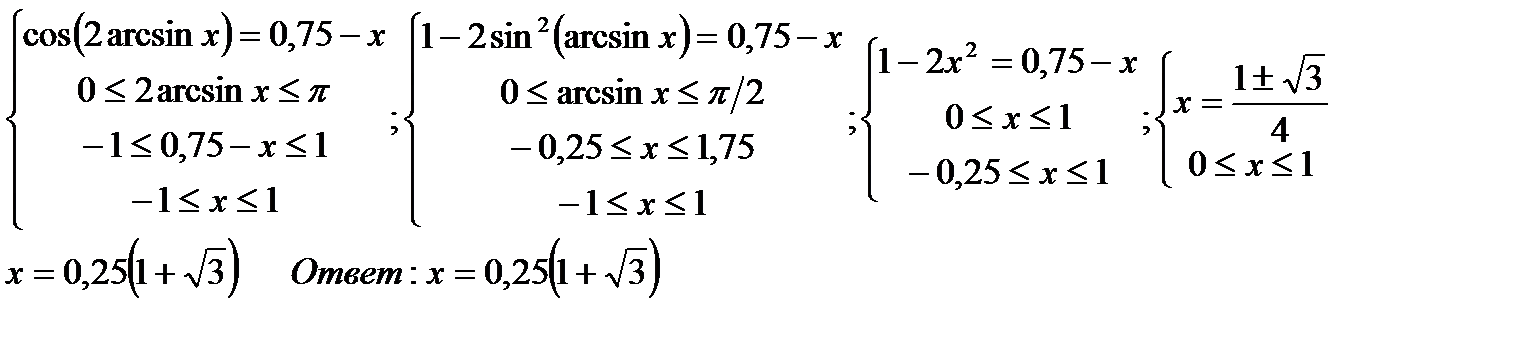
2) Уравнения с использованием формул 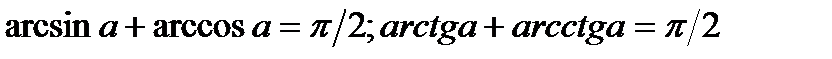
а) 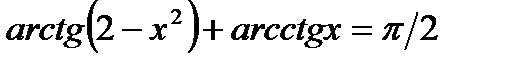
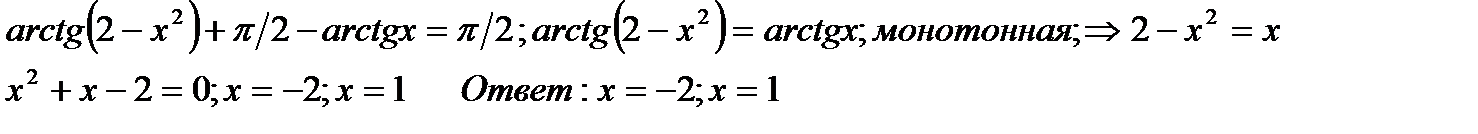
б) 
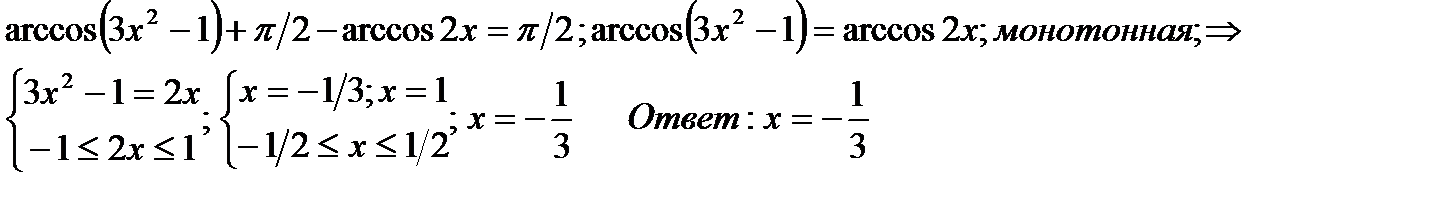
в) 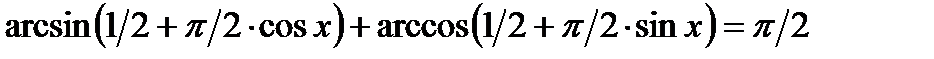
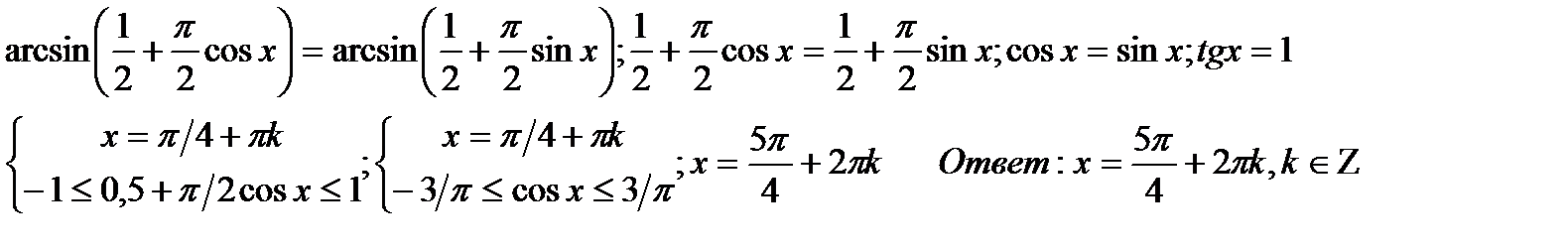
Квадратные уравнения
а) 

б)  (При решении ОДЗ не расширяется. Не находить)
(При решении ОДЗ не расширяется. Не находить)

4) 

Возьмём sin от обеих частей уравнения.

