Уравнения,решаемые с помощьюуниверсальнойтригонометрическойподстановки ( f(sinx, cosx, tgx, ctgx) )

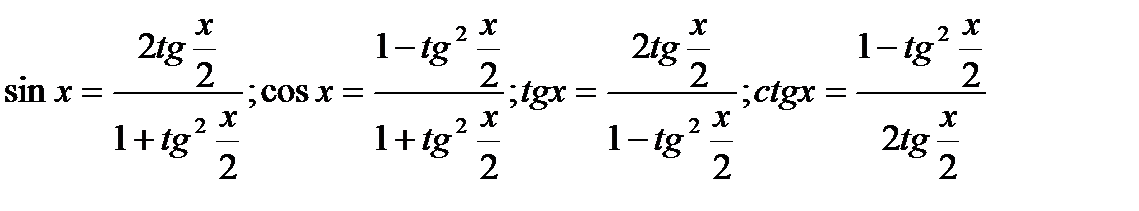
Замечание: эти формулы сужают ОДЗ. Можетпроизойтипотерякорней, т. к. tgx/2несуществуетприх = п + 2пк. Следовательно, эторешениенадопроверитьотдельно. Лучше, по возможности, не использовать эти формулы.

1 + cosx = sinx + tgxОДЗ: x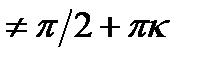

Проверяемподстановкойх = п + 2пк (0 = 0) – решение

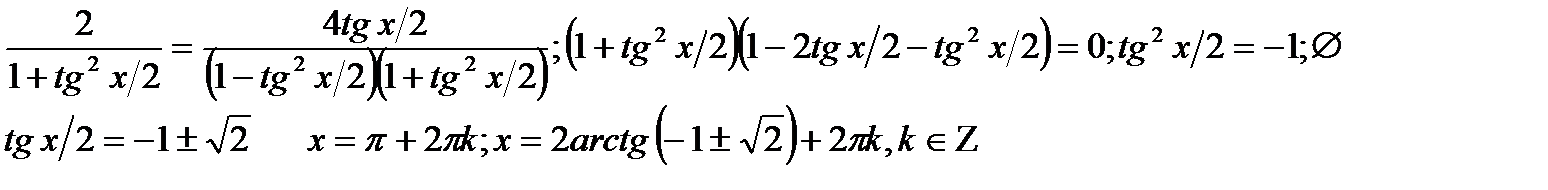
Ответ: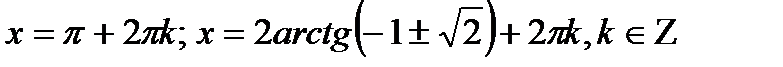

6) Уравнения, решаемые выделением тригонометрической единицы: sin²x + cos²x = 1

а)sin⁴x+ cos⁴x = sin2x – 1/2

1 – 2sin²xcos²x = sinxcosx – 1/2;t² + 2t – 3 = 0;D = 16;sin2x = - 3; 1;2x = п/2 + 2пk ,k

Ответ: x = п/4 + пk ,k

б)sin⁶x + cos⁶x – cos²2x = 1/16

(sin²x)³ + (cos²x)³ = 1 – 3/4 sin²2x;16 – 12sin²2x – 16cos²2x – 1 = 0; 4sin²2x = 1; sin2x =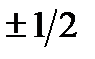

Ответ:x = 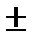п/12 + пk/2 ,k

Уравнения, в которых используются алгебраическая сумма и произведение тригонометрических функций.

а)sin2x – sinx – cosx – 1 = 0

sinx + cosx = t; t² = 1 + 2sinxcosx; sin2x = t² – 1; t² – t – 2 = 0;D = 9; t = 2; - 1

sinx + cosx = 2;sinx = 1иcosx = 1 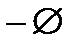sinx + cosx = - 1;sin(x + п/4) = - 1/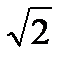

Ответ:x = (-1)^{к +1}п/4 – п/4 + пk, k

б) 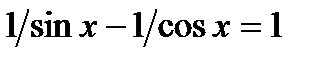ОДЗ: x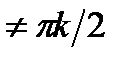

sinx - cosx = sinxcosx; sinx - cosx = t; t² = 1 - 2sinxcosx; sin2x = t² – 1; t² – t – 2 = 0; D = 8; 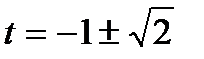; sinx - cosx = 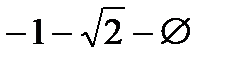;sinx - cosx = 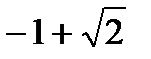;sin(x - п/4) =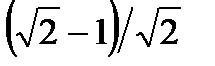

Ответ:x = (-1)^к 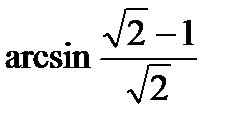+п/4 + пk, k

Уравнения,решаемыесиспользованиемформулпроизведенияфункций.

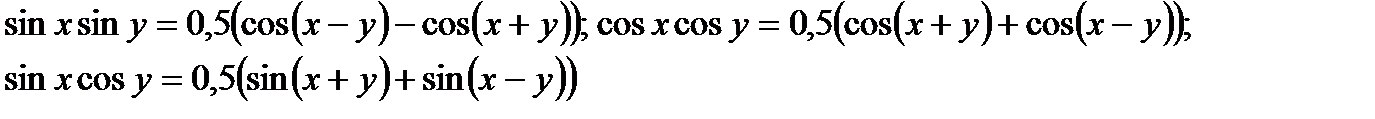
а)2sinx sin3x = cos2x

cos2x – cos4x – cos2x = 0;cos4x = 0;Ответ:x = п/8 + пk/4 ,k

б)сosx sin7x = cos3x sin5x

1/2(sin8x + sin6x) = 1/2(sin8x + sin2x); sin6x – sin2x = 0; sin2x cos4x = 0; sin2x = 0; cos4x = 0

Ответ: x = пk/2 ; x = п/8 + пk/4 ,k

9) Уравнениявидаasinx + bcosx = c, гдеa, b, c 0.

1)Переходкполовинномуаргументу (основнойспособрешения)

а)sinx + cosx = 1

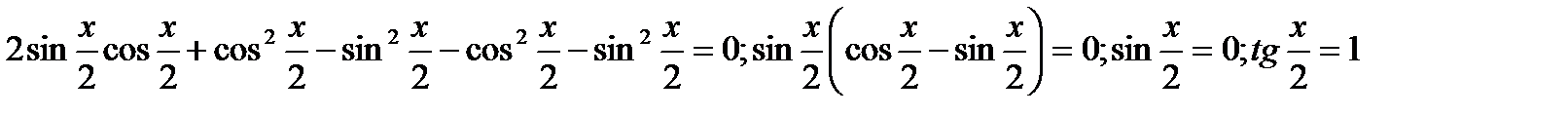
Ответ: x = 2пk ; x = п/2 + 2пk ,k

б)4sinx + 3cosx = 5

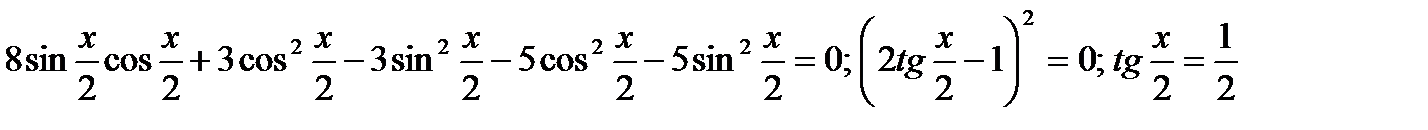Ответ:x =2arctg 1/2 + 2пk, k .

в)2sinx - 3cosx = 3

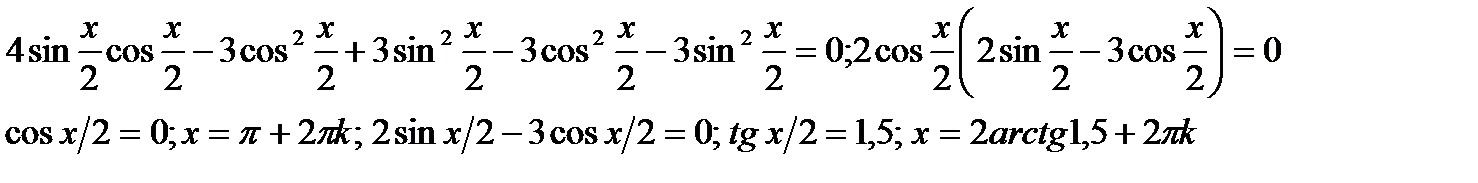Ответ: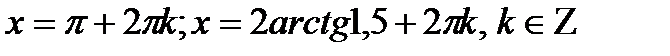

г)3sinx - 4cosx = 2

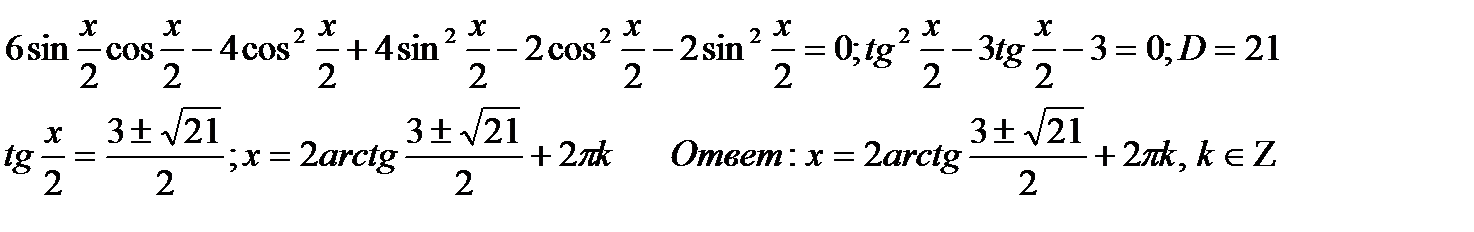
2)Делениеобеихчастейна 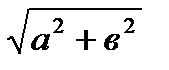(если«подгоняется»подформулу)

а)sinx + cosx = 1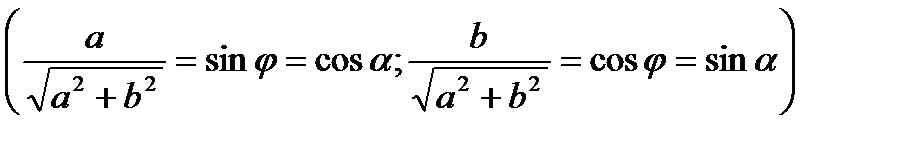

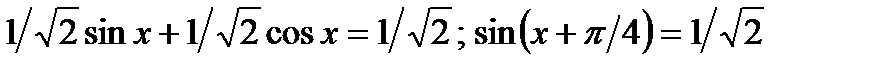;Ответ:x = (-1)^к п/4 – п/4 + пk, k

б) 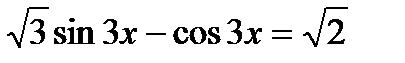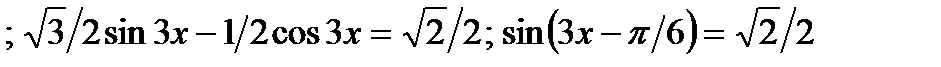Ответ:x = (-1)^к п/12 + п/18 + пk/3, k

3)Применениеуниверсальнойтригонометрическойподстановки

а)sinx + cosx = 1Проверяемх = п + 2пк; (-1 1)

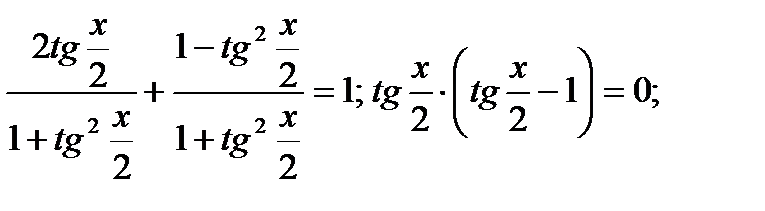Ответ: x = 2пk ; x = п/2 + 2пk ,k

б)2sinx - 3cosx = 3Проверяемх = п + 2пк;(3=3 – решение уравнения)

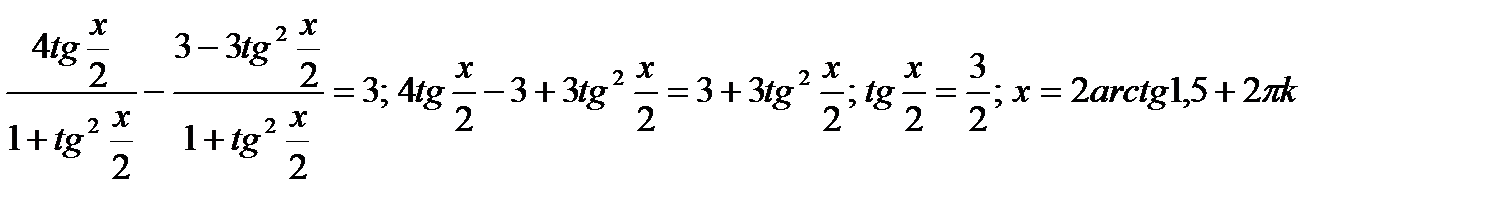Ответ: .

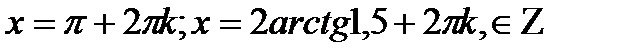4)Введениевспомогательногоуглаasinx + bcosx = 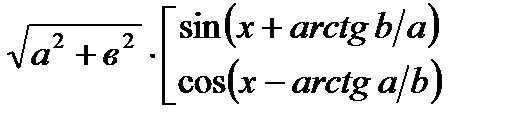Эти формулы удобно применять, если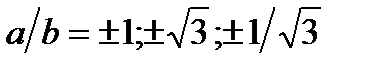

а)sinx + cosx = 1

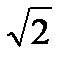sin(x + arctg 1) = 1; sin(x + п/4) = 1/ 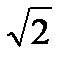Ответ:x = (-1)^к п/4 – п/4 + пk, k

б)сos3x - 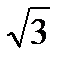sin3x = 1

2sin(-3x + arctg 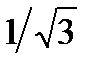) = 1; sin( п/6 – 3x) = 1/2Ответ:x = (-1)^к+1п/18+ п/18 – пk/3, k

в)2сos5x - 5sin5x =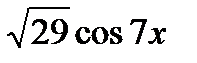

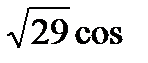(5x + arctg2,5 ) = 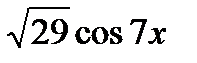;сos (5x + arctg2,5 ) - 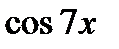=0; 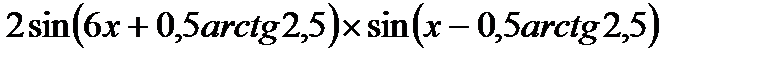= 0Ответ: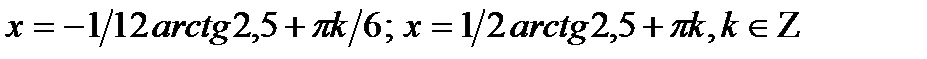

г)Найти множество значений функцииу = 2sinx - 3cosx

2sinx - 3cosx =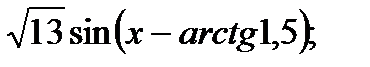

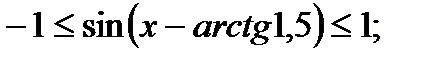
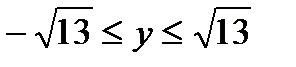
Метод оценки левой и правой частей уравнения.

а)cos3xcos2x=-1.

Первый способ.0,5 (cosx + cos 5x)=-1,cosx + cos 5x= -2.

Посколькуcos x ³ - 1, cos 5x ³ -1,заключаем,­ что cos x + cos 5x>-2;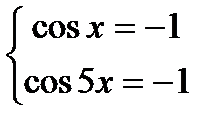

Решив уравнение cos x = -1, получимх=p + 2pк,гдеkÎZ.

Эти значенияхявляются также решениями уравненияcos 5x=-1,т.к.

cos 5x=cos 5 (p + 2pk)=cos(p + 4p + 10pk) = -1.х=p + 2pк, где kÎZ , -это все решения системы, а значит и исходного уравнения.Ответ:х =p (2k + 1),kÎZ

Второй способ. 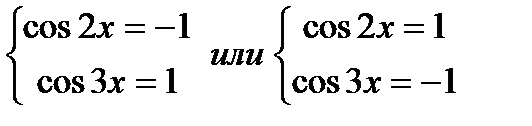Ответ: x = (2pк + 1), kÎZ

б)cos 3x + cos5x/2=2

Поскольку ½cos 3x½£ 1 и½cos 5x/2½£ 1 , то 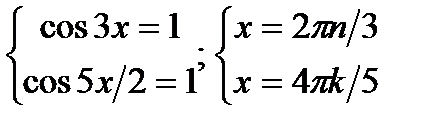Ответ:4pm, mÎZ

в)sinx + sin9x = 2

Таккак 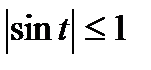, то 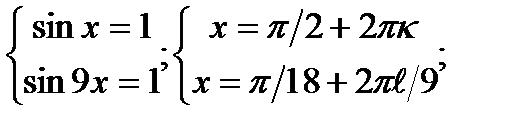Ответ:x = п/2 + 2пk ,k

г)sinx + cos4x = 2

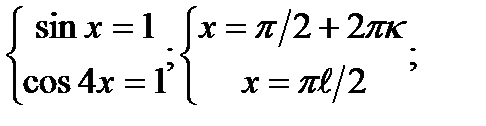Ответ:x = п/2 + 2пk ,k

д)sinxcos3x = -1

1) 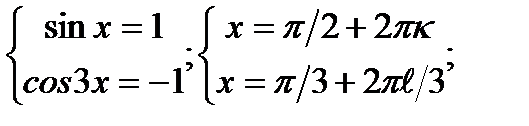2) 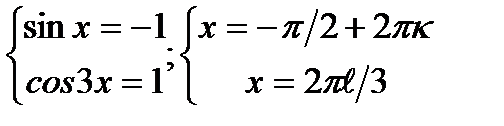Ответ:

е)sinxsin5x = 1

1) 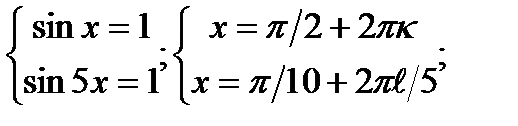2) 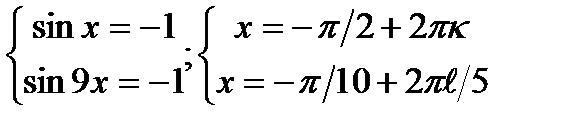Ответ: x = п/2 + пk

ж)sinxsin5xsin9x = 1

Решать аналогичног) – нерационально. Лучше проверить подстановкой 2 решения

sinx = 1; x = п/2 + 2пkиsinx = -1;x = - п/2 + 2пkОтвет:x = п/2 + 2пk , k

1)2 cos 3x+ 4 sin x/2 = 7Ответ:нет решений

2)2 cos 3x + 4 sin x/2 = -8Ответ:нет решений

3)3 cos 3x + cos x = 4Ответ:х=2pк, kÎZ

4)sin x sin 3 x=-1Ответ:х=p/2 + pк, kÎZ

5)cos⁸ x + sin⁷ x = 1Ответ:х=pm, mÎZ; х=p/2 + 2pn, nÎZ

6)cos 2x + cos3 x/4 - 2 = 0Ответ:8pк, kÎZ

7)cos²(2 x + p/3) + cos²( p/12 - x)=0Ответ:7p/12 + pк, kÎZ

8)cos 6x + sin5x/2 = 2Ответ:p+ 4pк, kÎZ