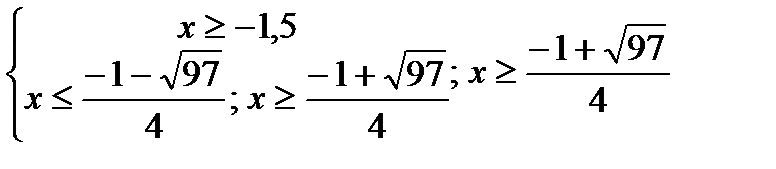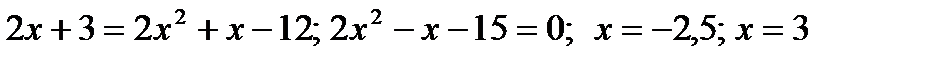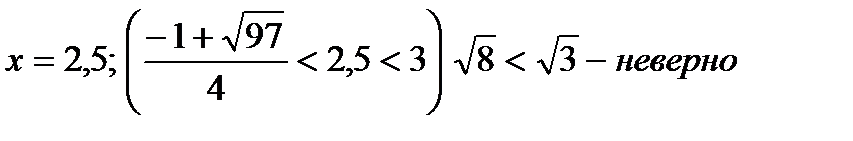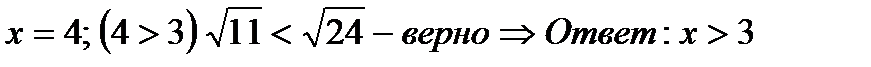Метод оценки левой и правой частей (метод мажорант).
Метод мажорант – метод нахождения ограниченности функции.Мажорирование –нахождение точек ограничения функции. М – мажоранта.
Если имеем f(x) = g(x) и известно ОДЗ, и если 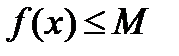 ,
, 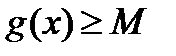 , то
, то 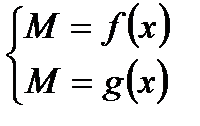
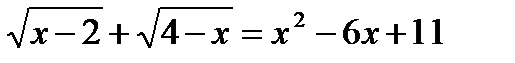 .
.
ОДЗ: 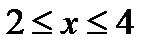 .
.
Рассмотримправую часть уравнения.Введем функцию 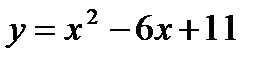 . Графиком является парабола с вершинойА(3; 2). Наименьшее значение функции у(3) = 2, то есть
. Графиком является парабола с вершинойА(3; 2). Наименьшее значение функции у(3) = 2, то есть 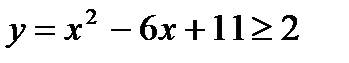 .
.
Рассмотрим левую часть уравнения. Введем функцию 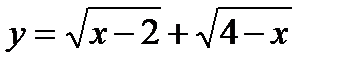 . С помощью производной нетрудно найти максимум функции, которая дифференцируема на x Î (2; 4).
. С помощью производной нетрудно найти максимум функции, которая дифференцируема на x Î (2; 4).
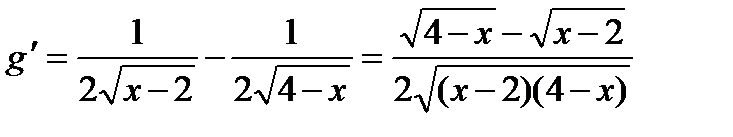 .
.
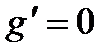 при
при 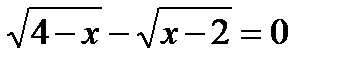 ,
,
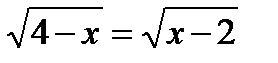 ,
,
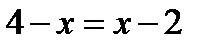 ,x=3.
,x=3.
g`+-
234
g
max
g(3)= 2.
Имеем, 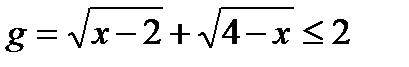 .В результате
.В результате 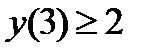 ,
, 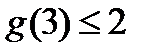 , то
, то 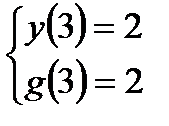
Составим систему уравнений, исходя из вышеуказанных условий: 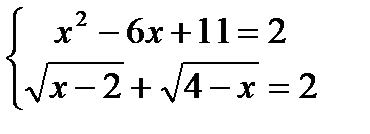
Решая первое уравнение системы, имеемх=3.Подстановкой этого значения во второе уравнение, убеждаемся, что х= 3есть решение системы.Ответ: х=3.
Применение монотонности функции.
а) 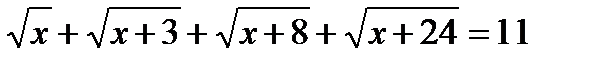
ОДЗ: 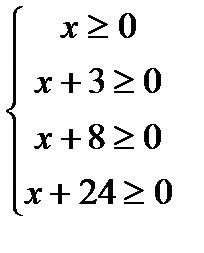 ,Þ
,Þ 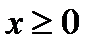 .
.
Известно, что сумма возрастающих функций есть функция возрастающая.
Левая часть представляет собой 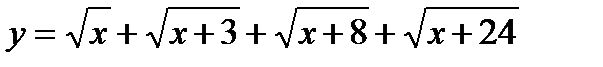 возрастающую функцию.Правая часть – линейная функция (к=0). Графическая интерпретация подсказывает, что корень единственный. Найдем его подбором, имеемх=1.
возрастающую функцию.Правая часть – линейная функция (к=0). Графическая интерпретация подсказывает, что корень единственный. Найдем его подбором, имеемх=1.
Доказательство:Предположим имеется корень х1, больший 1, тогда выполняется
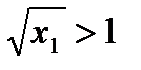 , т.к. х1>1,
, т.к. х1>1,
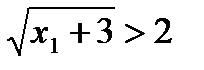 ,
, 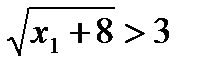 ,
, 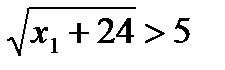 ,
, 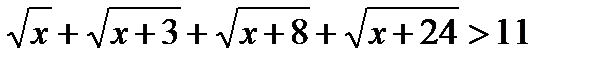 Делаем вывод, что корней больших единицы нет.Аналогично, можно доказать, что нет корней, меньших единицы.Значит x=1 – единственный корень.Ответ: x = 1.
Делаем вывод, что корней больших единицы нет.Аналогично, можно доказать, что нет корней, меньших единицы.Значит x=1 – единственный корень.Ответ: x = 1.
б) 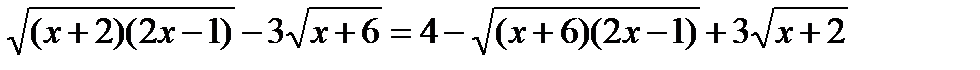
ОДЗ: 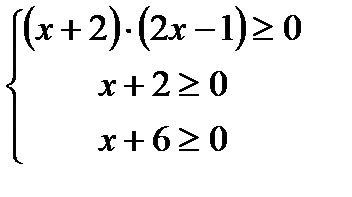 ,Þ
,Þ 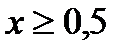 .
.
Преобразуем уравнение 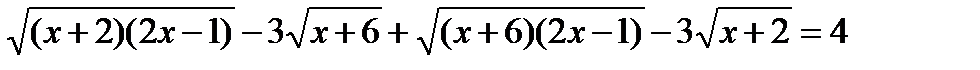 ,
,
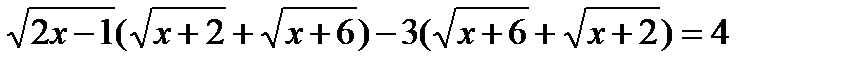 ,
, 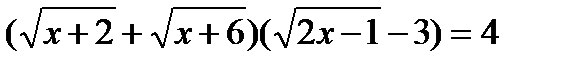
Левая часть представляет собой возрастающую функцию (произведение возрастающих функций), правая часть – линейная функция ( к = 0). Геометрическая интерпретация показывает, что исходное уравнение должно иметь единственный корень, который можно найти подбором,х=7.
Проверка: 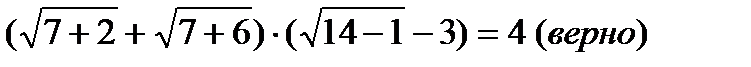
Можно доказать, что других корней нет (см. пример выше).Ответ:х=7.
ОСНОВНЫЕСПОСОБЫРЕШЕНИЯИРРАЦИОНАЛЬНЫХНЕРАВЕНСТВ
Как правило, обечастинеравенствавозводятсявнужнуюстепень. Невозможносделатьпроверку. Следовательно, необходимо следить, чтобыполучилосьнеравенстворавносильноеданному.
Привозведениивнечётнуюстепеньвсегдаполучаетсянеравенство равносильноеданному.
Привозведениивчётнуюстепеньнеравенствабудут равносильны, еслиобечастинеравенстванеотрицательны.
1)Неравенствавида 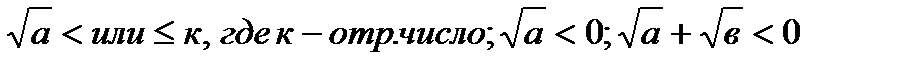 .Ответ:
.Ответ:
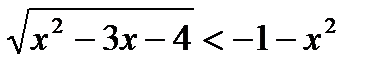 Ответ: решенийнет.
Ответ: решенийнет.
2)Неравенствавида 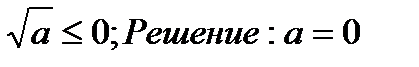
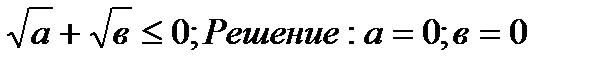
а) 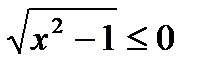 Ответ: х =
Ответ: х = 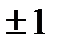
б) 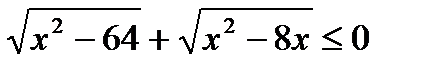 Ответ: х = 8
Ответ: х = 8
3)Неравенствавида 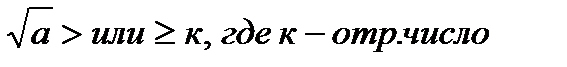 .
.
Ответ: ОДЗ
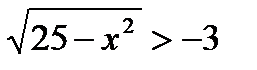 Ответ:
Ответ: 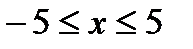
4)Неравенствавида 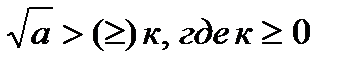
Решениемявляется неравенство: 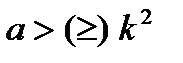
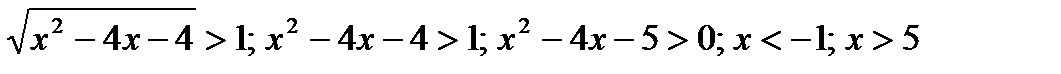 Ответ: х<-1;x>5
Ответ: х<-1;x>5
5)Неравенствавида 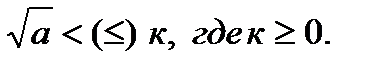
Решениемявляетсясистеманеравенств: 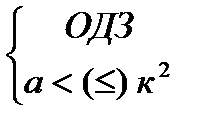
а) 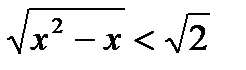 ;Система:
;Система: 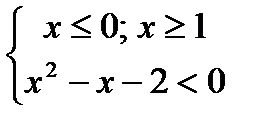 Ответ:
Ответ: 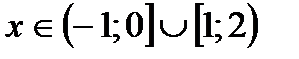
б) 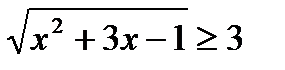 ;
; 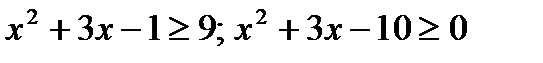 Ответ:
Ответ: 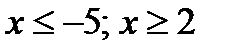
6)Неравенствавида 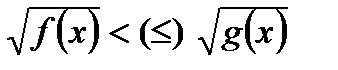
Решениемявляетсясистеманеравенств: 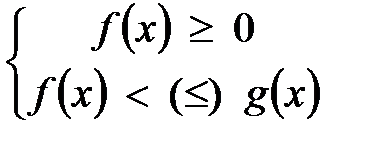
а) 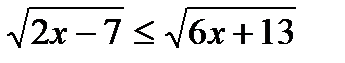 ;Система:
;Система: 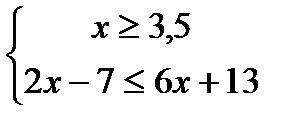 ;
; 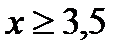 Ответ:
Ответ: 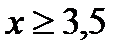
б) 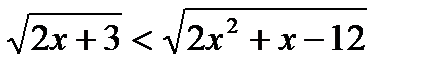 ;
; 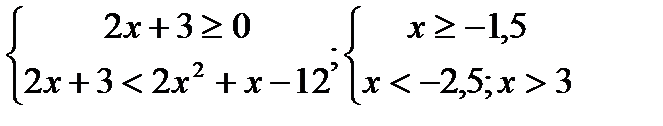 ;
; 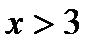 Ответ:
Ответ: 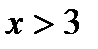
7)Неравенствавида 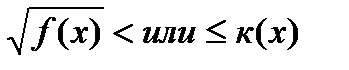
Решениемявляетсясистеманеравенств: 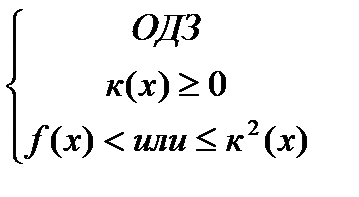
а) 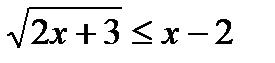 ;
; 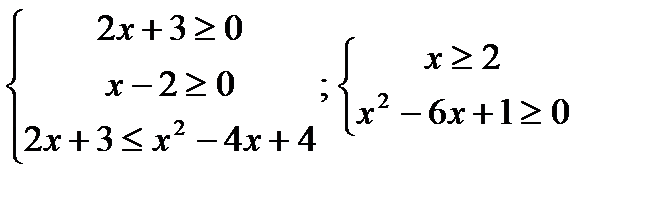 ;
; 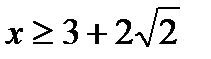 Ответ:
Ответ: 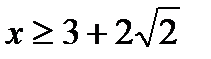
б) 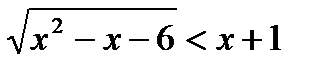 ;
; 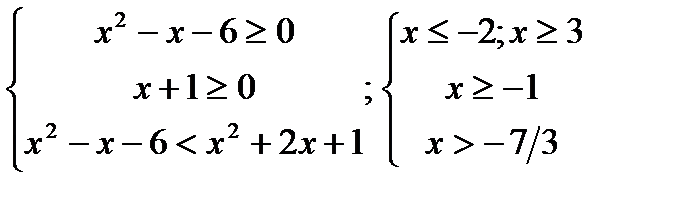 ;
; 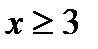 Ответ:
Ответ: 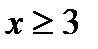
8)Неравенствавида 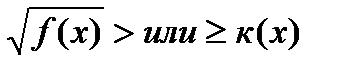
Решениемявляются 2 системынеравенств: 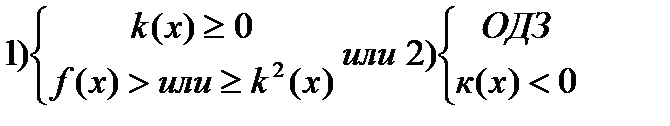
а) 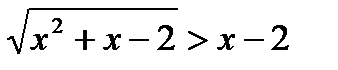
1) 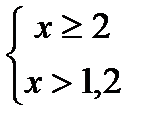 ;
; 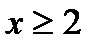 ;2)
;2) 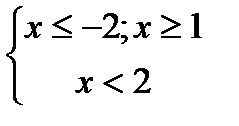 ;
; 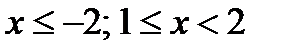 Ответ:
Ответ: 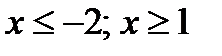
б) 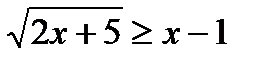
1) 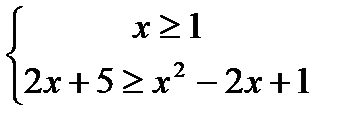 ;
; 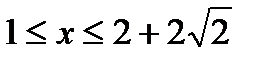 ; 2)
; 2) 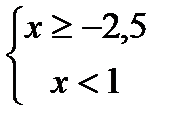 ;
; 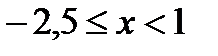 Ответ:
Ответ: 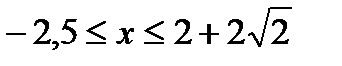
1) 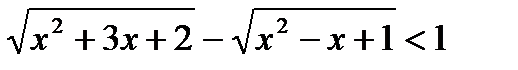
ОДЗ: 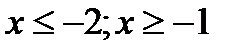
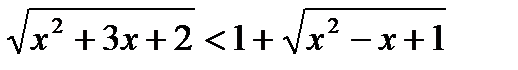 ;
; 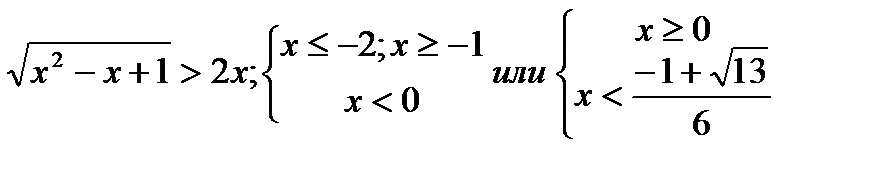 Ответ:
Ответ: 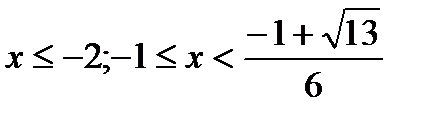
2)НайтиООФ:f(x) = 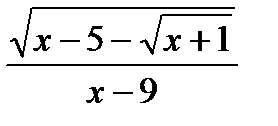
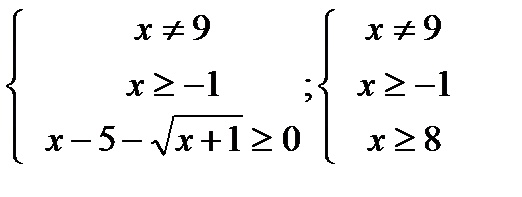 ;Ответ:x
;Ответ:x  9; x
9; x  8
8
3) 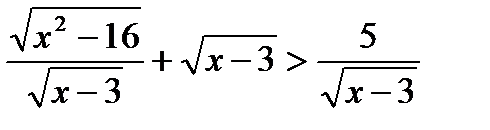 ;ОДЗ: х
;ОДЗ: х  4
4
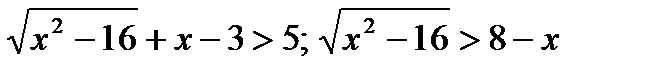
1) 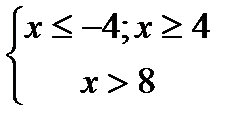 ;х > 82)
;х > 82) 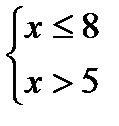 ;5 < х
;5 < х 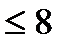 ;Ответ:х > 5
;Ответ:х > 5
4) 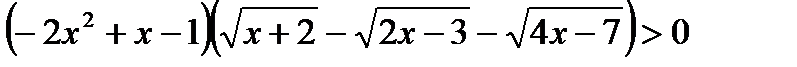 ;ОДЗ: х
;ОДЗ: х  1,75
1,75
-2x2 + x – 1 < 0 (D< 0); 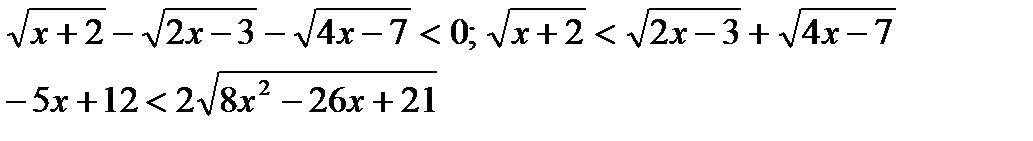
Решениемявляются 2 системынеравенств:1) 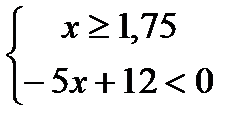 ; x> 2,4
; x> 2,4
2) 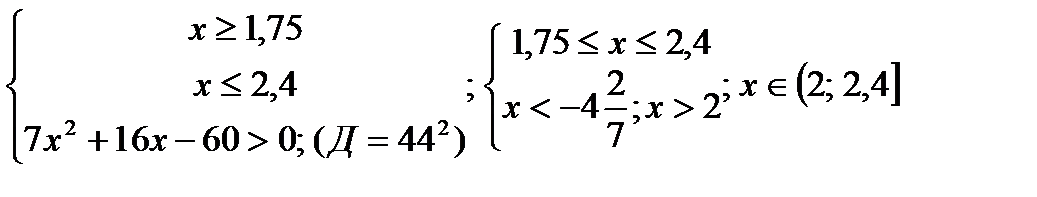 Ответ:х > 2
Ответ:х > 2
5) 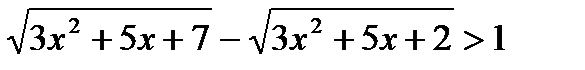
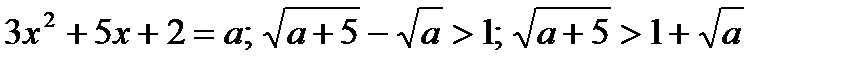 ;
; 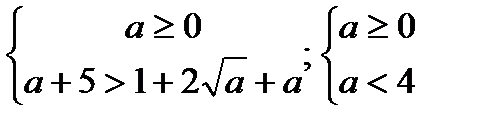
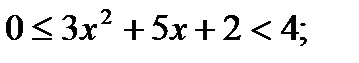
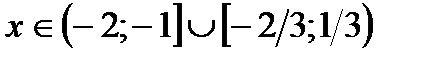 ;Ответ:
;Ответ: 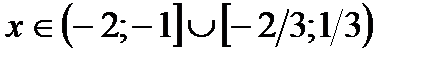
6)(х2 – 2х – 8)( 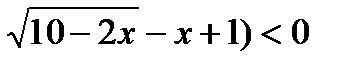 ;ОДЗ: х
;ОДЗ: х  5
5
Решениемявляются 2 системынеравенств.
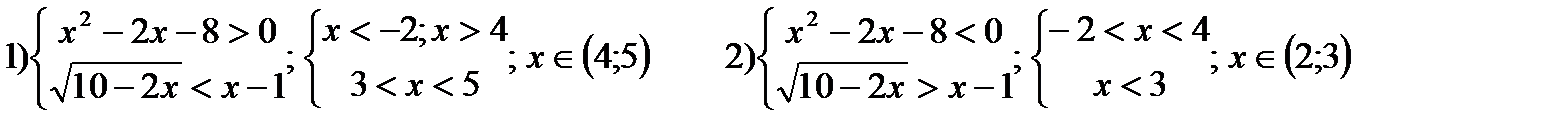 Ответ:
Ответ: 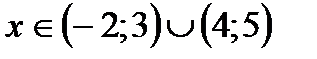
Метод интервалов
Алгоритм:1) ОДЗ
2) Решить уравнениеf(x) = g(x)
3) Подставить в исходное неравенство по одному значению из каждого изполучившихся интервалов (знаки не обязательно чередуются)
Если проверяемое значение удовлетворяет неравенству, то и все остальные значения соответствующего промежутка ему удовлетворяют.
Если проверяемое значение не удовлетворяет неравенству, то и никакое другое значение соответствующего промежутка ему не удовлетворяют.
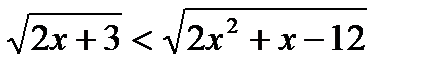
ОДЗ: