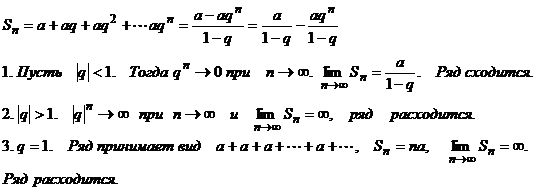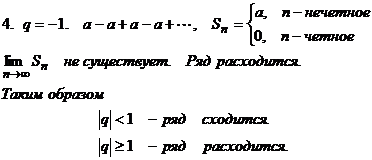Если существует конечный предел S последовательности частичных сумм данного ряда, то ряд называется сходящимся. В противном случае ряд называется расходящимся.

Ряды.

Понятие ряда возникает уже в элементарной математике, когда приходится решать задачу одного числа через другие более простые числа.

Н а п р и м е р . Выразить через десятичные дроби два числа ⁵/₈ и ⁵/₉ .

Эта сумма бесконечного множества слагаемых есть пример числового ряда.

Числовые ряды.

Пусть дана бесконечная последовательность чисел u₁, u₂, u₃,…, u_{n,… .}

Рассмотрим сумму u₁ + u₂ + u₃ + …+ u_n + …=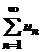

Эта сумма называется числовым рядом. Рассмотрим

S₁ = u₁,

S₂ = u₁ + u₂,

S₃ = u₁ + u₂ + u₃,

……………………

S_n = u₁ + u₂ + …+ u_n,

………………………..

Суммы S₁, S₂, … S_n, … называются частичными суммами.

Рассмотрим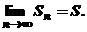

Определение.

Если существует конечный предел S последовательности частичных сумм данного ряда, то ряд называется сходящимся. В противном случае ряд называется расходящимся.

П р и м е р . Рассмотрим ряд

a + aq + aq² + aq³ + … + aqⁿ + …. Этот ряд называется геометрической прогрессией.

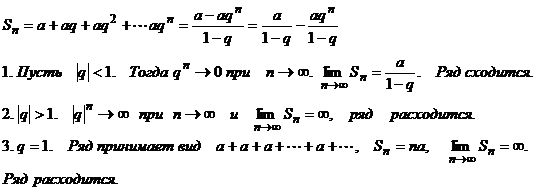
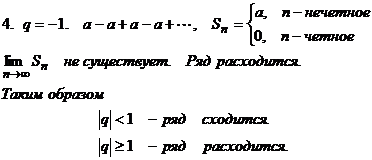
Необходимое условие сходимости ряда.

Теорема.

Если ряд сходится, то общий член его стремится к нулю при n→ ∞.

Выражение n-го члена при произвольном значении n называетсяобщим членом ряда.

Рассмотрим ряд

u₁ + u₂ + u₃ + … + u_n + ….

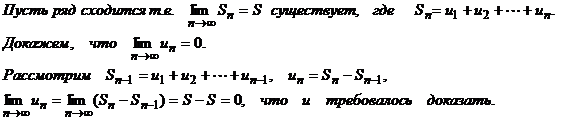
Это условие является только необходимым, но не является достаточным. Это означает, что изстремления к нулю общего членане следует сходимость ряда.

П р и м е р .

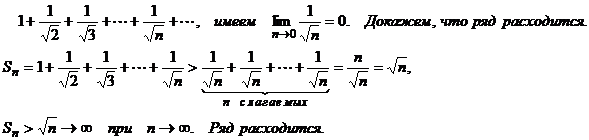
Следствие (достаточный признак расходимости).

Если общий член ряда не стремится к нулю при n→∞, то ряд расходится.

П р и м е р .

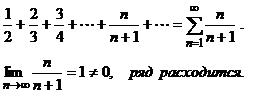
Ряды с положительными членами.

u₁ + u₂ + …+ u_n + … = 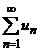(1)

Пусть u_n > 0 при произвольном n. Тогда S_n+1 = S_n + u_n+1 > S_n .

Последовательность частичных сумм знакоположительного ряда монотонно возрастает. Отсюда

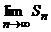- либо конечное число (если ряд сходится), либо ∞ (если ряд расходится)

Интегральный признак сходимости.

u₁ + u₂ + …+ u_n + … = 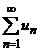(1)

Пусть члены ряда (1) положительны и не возрастают, т.е. u₁≥ u₂ ≥ u₃ ≥ …≥ u_n ≥ … и пусть f(x) – непрерывная невозрастающая функция x, такая, что f(1) = u₁, f(2) = u₂, …, f(n) = u_n, …

Тогда

Если несобственный интеграл 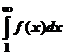сходится, то сходится и ряд (1).

Если этот интеграл расходится, то расходится и ряд (1).

Доказательство.

1. Пусть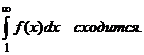

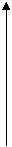
f(x)

u_n+1

u₁ u₂ u₃ u_n

1 2 3 … n n+1 x

S_ступ = u₂ + u₃ + … + u_n+1 = S_n+1 – u₁

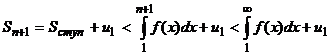
S_n+1 монотонно возрастает и остается ограниченной сверху, следовательно, 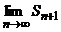существует, и ряд сходится.

2.

f(x)

u_n

u₁ u₂ u₃ u_n+1

1 2 3 … n n+1 x

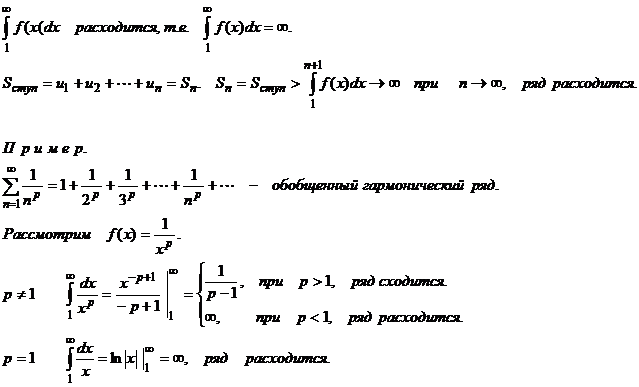
Таким образом, обобщенный гармонический ряд сходится приp > 1 и расходится при p ≤ 1.

Признаки сравнения.

Первый признак сравнения.

Пусть даны два положительных ряда.

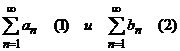
Если справедливо неравенство a_n≤ b_n(n = 1, 2, …), то из сходимости ряда (2) следует сходимость ряда (1), из расходимости ряда (1) следует расходимость ряда (2).

Доказательство.

1. Пусть ряд (2) сходится. S_n = a₁ + a₂ + …+ a_n,

S_n′ = b₁ + b₂ + … + b_n.

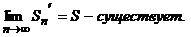
Очевидно, S_n^′ < S, т.к. S_n стремится к пределу, монотонно возрастая. Следовательно,

S_n ≤ S_n′ < S.

S_n монотонно возрастает и остается ограниченной. Следовательно,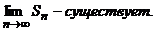

Ряд (1) сходится.

2. (1) – расходится. S_n′ ≥ S_n → ∞ при n → ∞, ряд (2) расходится.

Второй признак сравнения.

Пусть имеем два ряда (1) и (2). Если существует конечный, отличный от нуля предел 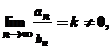то оба ряда либо одновременно сходятся, либо одновременно расходятся.

П р и м е р 1.

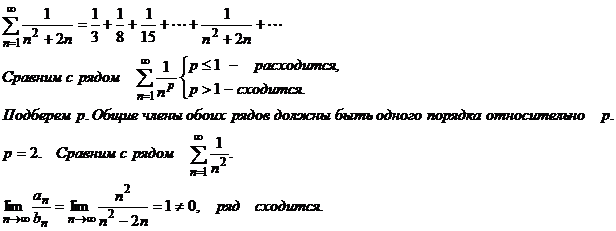
П р и м е р 2 .

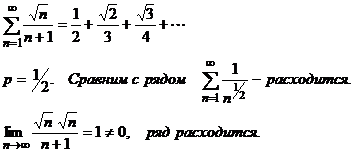
Признак Даламбера.

Если существует предел 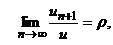(конечный или бесконечный) то, если ρ < 1, ряд сходится, если ρ > 1, то ряд расходится, если ρ =1, то признак не эффективен, ряд может сходиться, а может и расходиться.

1. ρ < 1. Рассмотрим ρ < q < 1. Тогда, начиная с некоторого N, выполняется неравенство

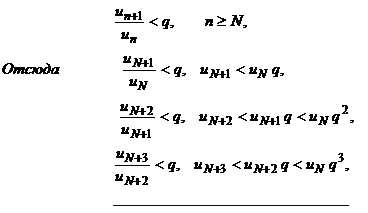
Рассмотрим ряд

u_N + u_N q + u_N q² + … (*)

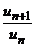
O ρ q 1 x

Ряд (*) – геометрическая прогрессия со знаменателем q< 1. Ряд сходится. Исходный ряд сходится по признаку сравнения.

2. ρ > 1. Тогда, начиная с некоторого n, справедливо неравенство 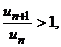т.е. u _n+1 > u _n. Следовательно, члены ряда возрастают, с возрастанием номера, общий не стремится к нулю, ряд расходится.

П р и м е р 1.

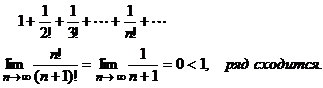
П р и м е р 2.

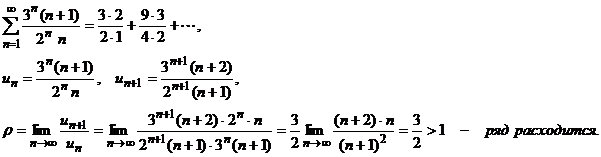
Знакочередующиеся ряды.

u₁ – u₂ + u₃ – u₄ + ∙∙∙ (1)

u_i > 0.

Признак Лейбница.

Если члены ряда (1) таковы, что u₁> u₂ > ∙∙∙ > u_n > ∙∙∙ и 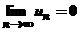, то ряд сходится, и сумма его не превышает первого члена.

n = 2m. Рассмотрим S_2m =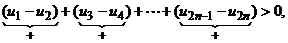

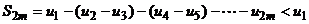. S_2m c возрастанием m монотонно возрастает и остается меньше u₁. Следовательно,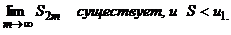

n = 2m + 1. S_2m+1 = S_2m + u_2m+1.

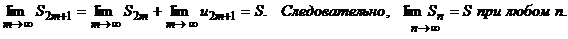
Ряд сходится, и сумма его меньше u₁.

П р и м е р .

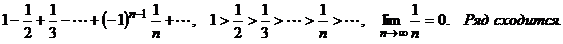
Абсолютная сходимость.

Рассмотрим ряд с произвольными членами.

u₁ + u₂ +…+ u _n + … (*)

u _n – произвольного знака. Рассмотрим другой ряд

|u₁| +| u₂| +…+| u _n| + … (**)

Теорема.

Функциональные ряды.

Рассмотрим ряд

u₁(x) + u₂(x) + … + u_n(x) + … (1)

Ряд (1) – функциональный ряд.

Введем понятие сходимости ряда (1). Зафиксируем значение x. Тогда

u₁(x) + u₂(x) + … + u_n(x) = S_n(x) – частичная сумма ряда. 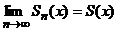- сумма ряда.

Таким образом, суммой S(x) функционального ряда является функция от x.

Если числовой ряд (2) сходится, то ряд (1) называется сходящимся в точке x .

A b

Полученный результат можно геометрически интерпретировать следующим образом. Рассмотрим график функции y = S(x). Построим около этой кривой полосу шириной 2ε, т.е. построим кривые y = S(x) + ε иy = S(x) – ε. Тогда при любом ε график функции s_n(x), будет лежать целиком в рассматриваемой полосе. В этой же полосе и будут лежать графики всех последующих частичных сумм.

Определение.

Функциональный ряд (1) называетсямажорируемымв некоторой области изменения х, если существует такой сходящийся числовой ряд

α₁ + α₂ + …+ α_n + … (2)

с положительными членами, что для всех х из данной области выполняются соотношения

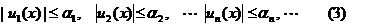
Пример.

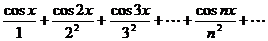
Ряд является мажорируемым на всей числовой оси. Действительно, для всех х выполняется условие

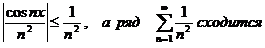
Непрерывность суммы ряда.

Сумма равномерно сходящегося ряда непрерывных функций есть функция непрерывная.

2. Равномерно сходящиеся ряды можно почленно интегрировать т.е.

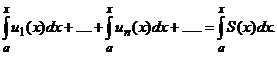
3. Равномерно сходящиеся ряды можно почленно дифференцировать т.е.

u₁′(x) + u₂′(x) + ....+ u_n′(x) +.... =S ′(x)

Степенные ряды.

Ряды.

Понятие ряда возникает уже в элементарной математике, когда приходится решать задачу одного числа через другие более простые числа.

Н а п р и м е р . Выразить через десятичные дроби два числа ⁵/₈ и ⁵/₉ .

Эта сумма бесконечного множества слагаемых есть пример числового ряда.

Числовые ряды.

Пусть дана бесконечная последовательность чисел u₁, u₂, u₃,…, u_{n,… .}

Рассмотрим сумму u₁ + u₂ + u₃ + …+ u_n + …=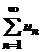

Эта сумма называется числовым рядом. Рассмотрим

S₁ = u₁,

S₂ = u₁ + u₂,

S₃ = u₁ + u₂ + u₃,

……………………

S_n = u₁ + u₂ + …+ u_n,

………………………..

Суммы S₁, S₂, … S_n, … называются частичными суммами.

Рассмотрим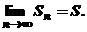

Определение.

Если существует конечный предел S последовательности частичных сумм данного ряда, то ряд называется сходящимся. В противном случае ряд называется расходящимся.

П р и м е р . Рассмотрим ряд

a + aq + aq² + aq³ + … + aqⁿ + …. Этот ряд называется геометрической прогрессией.