Теорема Дирихле о возможности перестановки местами членов ряда в сходящихся знакоположительных рядах.

Пусть - сходящийся знакоположительный ряд. Тогда его члены можно переставлять, менять местами, полученный ряд будет сходиться и иметь ту же сумму.

Доказательство. Проведем доказательство по индукции.

Пусть меняются местами два члена ряда 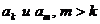. Тогда в исходном и полученном перестановкой членов ряде частичные суммы, начиная с 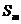будут совпадать. Следовательно, ряд, полученный перестановкой двух членов ряда, , будет сходиться и иметь ту же сумму.

Пусть при перестановке местами 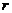членов ряда ряд сходится и имеет ту же сумму.

Пусть переставляются 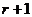членов ряда. Эта перестановка сводится к перестановке 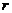членов ряда, а затем к перестановке еще какого-либо члена с каким-либо другим (перестановке двух членов ряда).

По индуктивному предположению при перестановке местами 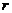членов ряда ряд сходится и имеет ту же сумму. Ряд, полученный перестановкой двух членов ряда, будет сходиться и иметь ту же сумму. Следовательно, и при перестановке 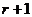членов ряда ряд будет сходиться и иметь ту же сумму.

Признак Лейбница.

Пусть

1. ряд имеет вид (знакочередующийся, )

2. последовательность монотонно убывает

3.

Тогда 1) ряд сходится

2)

Доказательство. Рассмотрим последовательность частичных сумм с четными номерами

(последовательность монотонно убывает по условию теоремы).

Т.е. последовательность ограничена сверху .

Т.е. последовательность монотонно возрастает.

По теореме Вейерштрасса существует .

Рассмотрим теперь последовательность частичных сумм с нечетными номерами

.

По условию , т.е. .

По доказанному выше . Следовательно, предел правой части равенства существует и равен . Поэтому предел левой части равенства тоже существует и равен

.

Раскроем определение предела как для четных n, так и для нечетных n. Следовательно, это справедливо для любых , поэтому .

Из доказанного выше неравенства . Переходя к пределу, получим .

Следствие. .Остаток ряда оценивается модулем первого отброшенного члена ряда.

Доказательство. Так как остаток знакочередующегося ряда тоже знакочередующийся ряд, то его сумма по признаку Лейбница оценивается модулем его первого члена.

То есть . А первый член остатка ряда и есть первый отброшенный член.

Пример. Ряд

. Ряд сходится по признаку Лейбница. Ряд из модулей – расходящийся гармонический ряд. Следовательно, ряд сходится условно.

. Функциональные ряды.

18.2.1. Основные определения. Пусть дана бесконечная последовательность функций .

независимой переменной х, имеющих общую область определения D. Ряд

называется функциональным рядом.

Примеры: 1. ;

2. ;

3. .

Для каждого значения функциональный ряд превращается в числовой ряд, сходящийся или расходящийся. Так, первый из примеров - геометрическая прогрессия со знаменателем х, этот ряд сходится при х=1/2 и расходится при х=2.

Определение. Значение , при котором функциональный ряд сходится, называется точкой сходимости функционального ряда. Множество всех точек сходимости функционального ряда называется областью сходимости этого ряда. Область сходимости обозначим .

Так, для первого из приведённых примеров область сходимости - интервал (-1, 1); для второго - ряда Дирихле - область сходимости - полуось х>0; третий ряд абсолютно сходится в любой точке х, так как при любом х справедливо ; следовательно, область сходимости третьего ряда ).

Для каждого мы получаем сходящийся числовой ряд, свой для каждого х, поэтому сумма функционального ряда есть функция 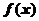, определённая на области . Так, для первого примера, как мы знаем, , т.е. на интервале

(-1, 1); вне этого интервала равенство не имеет места; так, в точке х=2 ряд расходится, а . Сумма второго ряда - знаменитая функция Римана , определённая на полуоси ; эта функция играет важную роль в теории чисел. Сумма третьего ряда, как мы увидим дальше при изучении рядов Фурье, равна функции периода , получающаяся в результате периодического повторения функции , определённой на отрезке , по всей числовой оси.

Коль скоро мы осознали, что сумма функционального ряда - функция, встаёт вопрос о свойствах этой функции. Так, члены ряда могут иметь свойства непрерывности, дифференцируемости, интегрируемости и т.д. Будет ли обладать этими свойствами сумма ряда? То, что это не праздный вопрос, показывает следующий пример. Пусть , , , , …, , …. Ряд 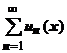состоит из непрерывных членов, найдём его область сходимости и сумму. Частичная сумма ряда . Последовательность при 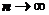имеет конечный предел только, если (это и есть область сходимости ряда), при этом Таким образом, для ряда, члены которого - непрерывные функции, мы получили разрывную на области сходимости сумму.

Сумма ряда сохраняет хорошие свойства своих членов в том случае, если ряд сходится равномерно.

18.2.2. Равномерная сходимость функционального ряда.Факт сходимости ряда 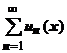к своей сумме 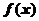в точке сходимости х означает, в соответствии с определением предела, то, что для любого числа существует такое натуральное N, что при n>N верно . Здесь - частичная сумма ряда в точке х. Число N зависит, естественно, от 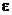, но оно зависит и от х, т.е. . В некоторых точках области сходимости ряд может сходиться к своей сумме быстро, т.е. неравенство будет выполняться при не очень больших значениях N, в других точках эта сходимость может быть медленной. Если ряд сходится к своей сумме примерно с одинаковой скоростью во всех точках х, то сходимость называется равномерной. Более точно, говорят, что ряд 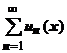сходится равномерно на области G, если для любого числа существует такое натуральное число , одно и то же для всех точек ,что при n>N выполняется неравенство (или, что тоже самое, , где - остаток ряда после n-го члена).

Понятие равномерной сходимости - одно из фундаментальных понятий функционального анализа. Именно равномерная сходимость обеспечивает сохранение суммой ряда хороших свойств своих членов. Чтобы осознать смысл и значение этого понятия, требуется время, которого у нас, к сожалению, нет. К счастью, имеется простой и понятный достаточный признак равномерной сходимости - признак Вейерштрасса.

Признак Вейерштрасса. Если существует такой положительный сходящийся числовой ряд , что члены функционального ряда 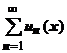в любой точке удовлетворяют неравенству , то функциональный ряд сходится равномерно в области G.

х

Числовой ряд, удовлетворяющий неравенству , называется мажорирующим рядом, или мажорантой функционального ряда; про функциональный ряд говорят, что он мажорируется числовым рядом.

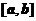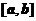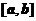Рассмотрим примеры, приведённые в начале раздела. Геометрическая прогрессия равномерно сходится на любом отрезке , целиком лежащем в области сходимости (-1,1). Действительно, построим мажоранту для геометрической прогрессии на . Из чисел а, b выберем большее по модулю. Пусть, например, . Тогда для любого выполняется . Таким образом, сходящийся (так как ) числовой ряд мажорирует на функциональный ряд , откуда, по признаку Вейерштрасса, следует равномерная сходимость этого функционального ряда.

Ряд равномерно сходится на любой полуоси , так как на этом множестве он мажорируется рядом .

Ряд равномерно сходится на всей числовой оси (мажоранта для этого ряда уже получена - это ряд ).