Аппроксимация ВАХ в окрестностях рабочей точки
 На практике часто приходится иметь дело с рабочей областью ВАХ настолько узкой, что можно считать, что изменение токов и напряжений происходит только в окрестностях некоторой рабочей точки. В таких случаях нет необходимости аппроксимировать ВАХ в широком диапазоне токов и напряжений, а достаточно ограничиться аппроксимацией лишь в окрестностях точки (рис.21.)
На практике часто приходится иметь дело с рабочей областью ВАХ настолько узкой, что можно считать, что изменение токов и напряжений происходит только в окрестностях некоторой рабочей точки. В таких случаях нет необходимости аппроксимировать ВАХ в широком диапазоне токов и напряжений, а достаточно ограничиться аппроксимацией лишь в окрестностях точки (рис.21.)
Пусть ток и напряжение в рабочей точке равны  ,
,  . Значение тока
. Значение тока 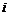 при изменении напряжения на
при изменении напряжения на  можно представить в виде ряда Тейлора:
можно представить в виде ряда Тейлора:
Рис.21. Аппроксимация в окрестностях
рабочей точки
 , (24)
, (24)
где  – значение тока в рабочей точке;
– значение тока в рабочей точке;

 − первая и вторая производная, определяемая с помощью формул численного дифференцирования:
− первая и вторая производная, определяемая с помощью формул численного дифференцирования:
 ; (25)
; (25)
 . (26)
. (26)
Вводя обозначения:
 ,
,  ,
,  , (27)
, (27)
уравнение (24) можно представить в виде:
 (28)
(28)
Как правило, при аппроксимации ВАХ нелинейных резистивных элементов в окрестностях рабочей точки используются полиномы низких степеней и весьма часто полиномом первой степени:
 . (29)
. (29)
Последнее уравнение представляет уравнение прямой линии. Если ВАХ задана графически, то для определения коэффициента  достаточно провести касательную к ВАХ и по уравнению:
достаточно провести касательную к ВАХ и по уравнению:
 . (30)
. (30)
В машинном анализе наибольшее распространение получила сплайн аппроксимация, т.е. аппроксимация полиномом второй степени:
 . (31)
. (31)
МАГНИТНЫЕ ЦЕПИ
Основные понятия
В современных электронных устройствах для увеличения магнитного потока в определенной части пространства используют ферромагнитные материалы. Устройства или их совокупность, содержащие ферромагнитные материалы, предназначенные для создания с помощью намагничивающей силы магнитного потока, называют магнитной цепью.
Магнитное поле характеризуется вектором магнитной индукции 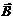 . По принципу суперпозиции внутри вещества, магнитное поле складывается из внешнего поля и наведенного им (по гипотезе Ампера):
. По принципу суперпозиции внутри вещества, магнитное поле складывается из внешнего поля и наведенного им (по гипотезе Ампера):
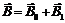 , (31)
, (31)
где 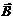 - магнитная индукция внутри вещества;
- магнитная индукция внутри вещества;
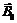 - магнитная индукция внешнего поля в вакууме;
- магнитная индукция внешнего поля в вакууме;
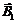 - магнитная индукция наведенного поля, определяется магнитными свойствами вещества.
- магнитная индукция наведенного поля, определяется магнитными свойствами вещества.
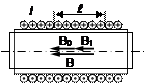 Если внешнее поле создается бесконечной катушкой, витки которой навиты вплотную друг к другу, то согласно закону Био-Савара:
Если внешнее поле создается бесконечной катушкой, витки которой навиты вплотную друг к другу, то согласно закону Био-Савара:
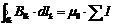 , (32)
, (32)
Рис. 22. Катушка с сердечником
где 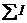 - алгебраическая сумма токов, пронизывающие поверхность, ограниченные контуром
- алгебраическая сумма токов, пронизывающие поверхность, ограниченные контуром 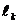 ;
;
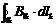 - циркуляция вектора магнитной индукции по замкнутому контору;
- циркуляция вектора магнитной индукции по замкнутому контору;
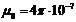 - магнитная постоянна [Гн/м].
- магнитная постоянна [Гн/м].
Магнитное поле бесконечной катушки однородное, поэтому выражение (32) можно записать:
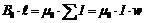 , (33)
, (33)
где 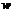 – число витков катушки, уложенных на участке длинной
– число витков катушки, уложенных на участке длинной 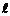 ;
;
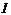 - величина тока в катушке;
- величина тока в катушке;
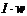 - намагничивающий ток.
- намагничивающий ток.
Введем понятие вектора напряженности магнитного поля 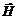 , который не зависит от свойств среды (вещества), и определяется только токами в проводах:
, который не зависит от свойств среды (вещества), и определяется только токами в проводах:
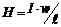 . (34)
. (34)
Намагниченность вещества является результатом действия внешнего магнитного поля:
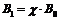 , (35)
, (35)
где 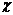 - магнитная восприимчивость вещества.
- магнитная восприимчивость вещества.
Учитывая (35), выражение (31) можно переписать в виде:
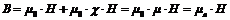 , (36)
, (36)
где 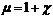 − относительная магнитная проницаемость ;
− относительная магнитная проницаемость ;
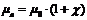 − абсолютная магнитная проницаемость.
− абсолютная магнитная проницаемость.
Магнитная проницаемость 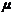 зависит от строения вещества и в общем случае изменяется с изменением
зависит от строения вещества и в общем случае изменяется с изменением 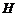 , т.е. зависимость
, т.е. зависимость 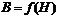 является нелинейной. Эта зависимость не имеет точного аналитического выражения и поэтому ее изображают для каждого ферромагнитного материала в виде кривой намагничивания, определяемой опытным путем.
является нелинейной. Эта зависимость не имеет точного аналитического выражения и поэтому ее изображают для каждого ферромагнитного материала в виде кривой намагничивания, определяемой опытным путем.
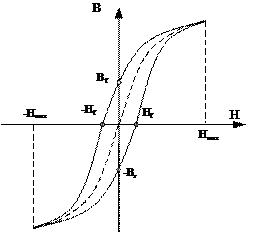
Рис. 23. Кривая намагничивания ферромагнитного материала
Если изменять 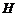 от
от 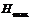 до
до 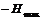 , то после нескольких циклов перемагничивания можно получить замкнутую петлю гистерезиса (рис.23). На этом рисунке
, то после нескольких циклов перемагничивания можно получить замкнутую петлю гистерезиса (рис.23). На этом рисунке 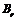 – остаточная индукция,
– остаточная индукция, 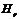 – коэрцитивная сила.Основной кривой намагниченности называют геометрическое место вершин замкнутых симметричных петель гистерезиса, снятых при различных
– коэрцитивная сила.Основной кривой намагниченности называют геометрическое место вершин замкнутых симметричных петель гистерезиса, снятых при различных 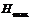 (см.рис.23 -пунктирная кривая).
(см.рис.23 -пунктирная кривая).
