Нелинейные элементы и их характеристики

Методы расчета резистивных нелинейных

Цепей постоянного тока

Электрическая цепь, содержащая хотя бы один нелинейный элемент, называется нелинейной.

Выделим два основных подхода, используемых для расчета и анализа нелинейных электрически цепей. Первый подход основан на графическом решении. Второй – аналитическое решение с использованием аппроксимирующих функций. Расчет нелинейных цепей обоими методами рассмотрен ниже на конкретных примерах.

Расчет цепей при последовательном соединении нелинейных элементов

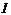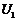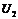Рассмотрим цепь, (рис.5) с двумя последовательно соединёнными нелинейными элементами, ВАХ которых приведены на рис.6. Требуется определить ток цепи и напряжение на элементах и при заданной э.д.с. .

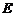Рис.5. Цепь с последовательным Рис.6. ВАХ нелинейных

соединением нелинейных элементов элементов

Согласно второму закону Кирхгофа:

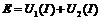. (5)

Для решения уравнения (5) необходимо графическим путём найти сумму 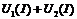. Для этого, задаваясь рядом значений тока ( 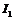, , 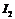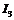и т.д., чем больше значений, тем точнее построим линию суммы), следует сложить ординаты ВАХ, как это сделано на рис.7.

Рис.7. Пояснение к решению задачи.

Таким образом участок цепи с двумя элементами заменили одним нелинейным элементом, имеющим ВАХ 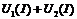. Построив горизонтальную линию 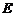, нетрудно определить ток 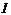, опустив перпендикуляр из точки пересечения А, и найти напряжение 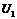и 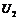на нелинейных элементах (определив ординаты точек Б и С).

Аналогичным образом можно решить задачу, если одно из нелинейных сопротивлений будет линейным, или цепь содержит не два нелинейных элемента, а несколько, последовательно соединённых.

Расчет цепей с параллельным соединением нелинейных элементов

Рассмотрим цепь, содержащую два параллельных нелинейных эле-мента (рис.8.а), ВАХ которых приведены на рис.8.б.

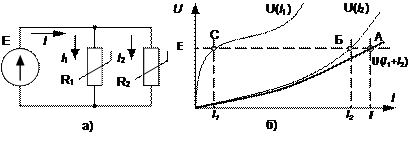
Рис.8. Расчет цепи при параллельном соединении элементов:

а) схема цепи; б) ВАХ элементов

Так как 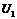= = 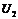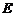, а 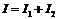, то для нахождения результирующей ВАХ складываем абсциссы (токи) ВАХ 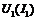, 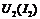при одинаковых ординатах (напряжениях). Значение тока находим графическим путем с помощью результирующей ВАХ 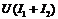, как абсциссу пересечения с горизонтальной линией Е (точка А). Токи ветвей – точки С и Б соответственно.

Анализ разветвленных цепей

Расчет разветвленных цепей графическим способом рассмотрим на конкретном примере цепи на рис.14.а. ВАХ нелинейных элементов для упрощения графических построений приняты одинаковыми и приведены на рис. 6.14.б.

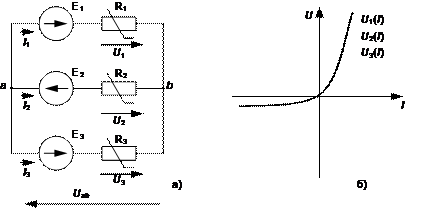
Рис.14. Расчет разветвленной цепи

а) схема цепи; б) ВАХ нелинейных элементов

Выбираем положительное направление токов в ветвях. Согласно второму закону Кирхгофа для напряжения 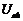можем записать:

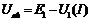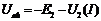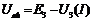; ; . (7)

Считая каждую ветвь активным двухполюсником, строим их ВАХ. (см. рис.15.). ВАХ двухполюсника получается сдвигом ВАХ резистивного элемента на соответствующую ЭДС. Предварительно ВАХ резистивного элемента необходимо отразить относительно оси абсцисс, т.к. в уравнения (7) они входят со знаком минус.

Согласно первому закону Кирхгофа имеем:

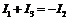. (8)

Поэтому для нахождения точки установившегося режима строим вспомогательную кривую 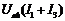, для чего при одинаковых напряжениях складываем абсциссы кривых 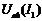и .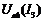

Рис.15. Построение для разветвленной цепи

Точка пересечения кривых 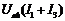и 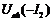- точка А и определяет решение: напряжение 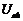, токи ветвей , , .

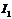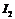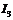МАГНИТНЫЕ ЦЕПИ

Основные понятия

В современных электронных устройствах для увеличения магнитного потока в определенной части пространства используют ферромагнитные материалы. Устройства или их совокупность, содержащие ферромагнитные материалы, предназначенные для создания с помощью намагничивающей силы магнитного потока, называют магнитной цепью.

Магнитное поле характеризуется вектором магнитной индукции 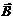. По принципу суперпозиции внутри вещества, магнитное поле складывается из внешнего поля и наведенного им (по гипотезе Ампера):

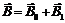, (31)

где 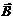- магнитная индукция внутри вещества;

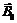- магнитная индукция внешнего поля в вакууме;

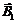- магнитная индукция наведенного поля, определяется магнитными свойствами вещества.

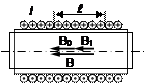Если внешнее поле создается бесконечной катушкой, витки которой навиты вплотную друг к другу, то согласно закону Био-Савара:

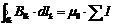, (32)

Рис. 22. Катушка с сердечником

где 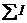- алгебраическая сумма токов, пронизывающие поверхность, ограниченные контуром ;

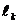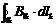- циркуляция вектора магнитной индукции по замкнутому контору;

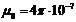- магнитная постоянна [Гн/м].

Магнитное поле бесконечной катушки однородное, поэтому выражение (32) можно записать:

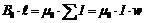, (33)

где 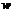– число витков катушки, уложенных на участке длинной ;

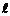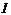- величина тока в катушке;

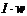- намагничивающий ток.

Введем понятие вектора напряженности магнитного поля 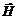, который не зависит от свойств среды (вещества), и определяется только токами в проводах:

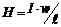. (34)

Намагниченность вещества является результатом действия внешнего магнитного поля:

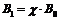, (35)

где 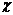- магнитная восприимчивость вещества.

Учитывая (35), выражение (31) можно переписать в виде:

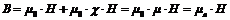, (36)

где 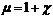− относительная магнитная проницаемость ;

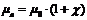− абсолютная магнитная проницаемость.

Магнитная проницаемость 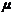зависит от строения вещества и в общем случае изменяется с изменением 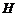, т.е. зависимость 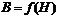является нелинейной. Эта зависимость не имеет точного аналитического выражения и поэтому ее изображают для каждого ферромагнитного материала в виде кривой намагничивания, определяемой опытным путем.

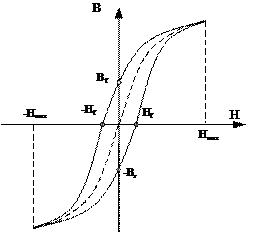
Рис. 23. Кривая намагничивания ферромагнитного материала

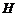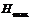Если изменять от до 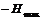, то после нескольких циклов перемагничивания можно получить замкнутую петлю гистерезиса (рис.23). На этом рисунке 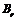– остаточная индукция, 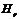– коэрцитивная сила.Основной кривой намагниченности называют геометрическое место вершин замкнутых симметричных петель гистерезиса, снятых при различных 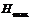(см.рис.23 -пунктирная кривая).

Феррорезонанс напряжений

В электрических цепях, содержащих катушки с сердечниками и конденсаторы, наблюдаются особые явления, связанные с нелинейными свойствами катушек.

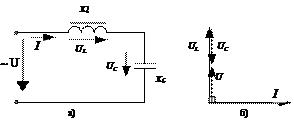
Рис.44. Цепь с феррорезонансом напряжений

а) схема цепи; б) векторная диаграмма

Рассмотрим явление, возникающие в цепи, состоящей из последовательного соединения катушки и конденсатора (рис.44.а).

Предположим, что в катушке отсутствуют потери энергии. В этом случае, напряжение на катушки 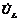опережает ток на 90^о, 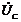отстает от тока также на 90^о. Векторная диаграмма для такой цепи представлена на рис.44.б, из которой можно записать:

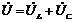. (62)

Представим на рис.45.а зависимост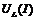и и 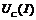. Первая зависимость нелинейная и определяется видом кривой намагничивания. Результирующая зависимость 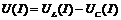является также нелинейной (см.рис.45.а).

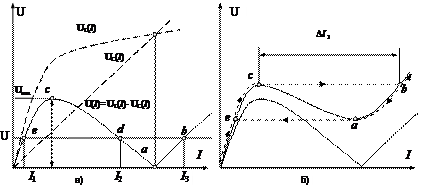
Рис.45. Феррорезонанс напряжений

а) для идеализированной цепи; б) с учетом потерь

Согласно полученной характеристике при заданном значение напряжения 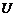возможно три установившихся режима цепи с токами 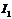, , 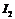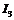. Если приложенное напряжение больше 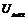, то возможен только один определенный режим, при этом общий характер цепи емкостный.

Особая точка «а» является точкой резонанса, в этой точке 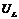= 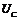. В отличие от цепей с постоянными параметрами, резонанс в рассматриваемой цепи можно достичь изменением напряжения, так как индуктивность катушки зависит от протекающего тока. Это явление получило название феррорезонанса напряжения.

Область «ас» характеристики 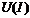является областью неустойчивых режимов. Действительно пусть установившийся режим характеризуется точкой «d». Тогда всякое случайное повышение тока приведет к уменьшению падения напряжения в цепи и к дальнейшему увеличению тока. Всякое случайное уменьшение тока, переводит состояние цепи из режима «d» в режим «e». Вследствие наличия в цепи потерь и высших гармоник, фактическая характеристика 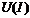цепи приобретает вид, указанный на рис.45.б. Опытным путем при изменении напряжения 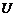, можно снять только часть характеристики. Участок «сb» при повышении напряжения снять нельзя, т.к. из точки «с» происходит срыв в точку «b», сопровождаемый скачком тока 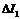и изменением знака угла сдвига в цепи. При уменьшении тока происходит срыв из точки «a» в точку «e».

Построить характеристику 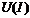для цепи, содержащей сопротивление 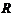можно провести следующим образом:

1. Строят характеристику .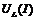

2. Строят характеристику .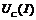

3. Графическим путем находят характеристику .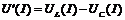

4. Задаются рядом значений тока 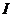и находят из характеристики 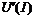. Напряжение сети находят по уравнению 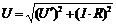, и строят зависимость .

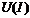3.3.6 Феррорезонанс токов.

Схема цепи, в которой возможен резонанс токов, приведена на рис.46.а. Как и при резонансе напряжений, пренебрежем потерями в цепи и наличием высших гармоник. Векторная диаграмма цепи представлена на рис.46.б. Из диаграммы:

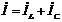. (63)

Общий ток 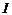может быть как отстающим, так и опережающим. На рис.47.а построена ВАХ катушки и конденсаторы 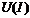путем графического вычитания абсцисс 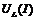и .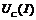

Рис. 46. Цепь с феррорезонансом токов

а) схема цепи; б) векторная диаграмма

Из рис.47.а видно, что при некоторых заданных токах установившийся режим может существовать при трех различных напряжениях , , .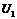

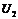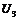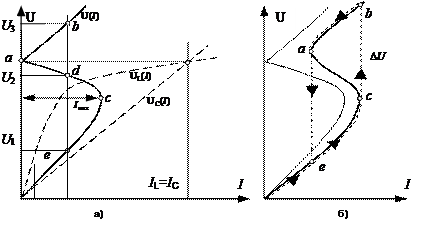
Рис.47. Феррорезонанс токов

а) для идеализированной цепи; б) с учетом потерь

Особая точка «а» является точкой резонанса токов. Отсюда следует, что в данной цепи в отличие от линейных цепей, резонанс можно достичь изменением напряжения. Это явление получило название феррорезонанса токов. В реальной цепи вследствии наличия потерь и высших гармоник, ВАХ видоизменяется (рис.47.б). При постепенном увеличении тока в цепи, а также и при уменьшении его, будут происходить срывы, аналогичные рассмотренным ранее, и также сопровождающиеся изменением знака угла сдвига в цепи. Для получения точек срывов необходимо иметь источник с регулируемым выходным током, а не напряжением.

Практически это можно осуществить, если последовательно с регулируемым источником включить большое линейное сопротивление.

Метод условной линеаризации

Основная идея метода условной линеаризации состоит в замене нелинейной характеристики отрезком прямой на ее рабочем участке. Рассмотрим применение данного метода на примере.

Пример 15.Найти закон изменение напряжения на конденсаторе при замыкании ключа в цепи на рис.68.а ВАХ диода приведена на рис.68.б.

Решение.Для нахождения рабочих точек на ВАХ диода до замыкания и после замыкания ключа применим метод эквивалентного генератора. Заменим всю цепь, кроме ветви с вентилем (нелинейное сопротивление) активным двухполюсником (рис.69).

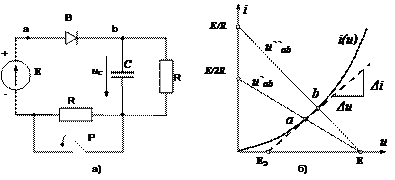
Рис.68. Схема цепи и ВАХ диода

Напряжение u_ab при разомкнутом ключе:

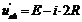. (94)

Конденсатор на установившийся режим при постоянной ЭДС не оказывает влияние. Напряжение U_ab при замкнутом ключе:

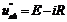. (95)

Получили два уравнения прямой линии. Эти две прямые построены на рис.68.б.

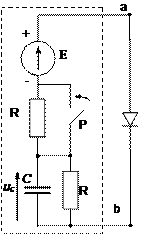При .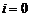

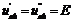При :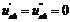

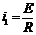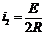, . (96)

Точки пересечения этих прямых с ВАХ диода дают установившиеся значения напряжения и тока до и после замыкания ключа, т.е. определяют предельные значения напряжения на диоде. Проведя прямую через эти точки a и b, мы условно линеаризируем ВАХ в рабочей зоне. Уравнение прямой:

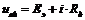, (97)

где 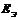, 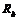- параметры схемы замещения диода.

Рис.69. Эквивалентный двухполюсник

Дифференциальное сопротивление диода 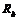- определяют из ВАХ:

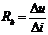. (98)

Диод замещают источником ЭДС 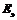, включенной последовательно с линейным сопротивлением 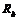. (рис.70)

В итоге исходную нелинейную цепь можно представить в виде линейной цепи, для которой переходная функция напряжения конденсатора определяется уравнением:

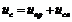. (99)

Рис.70. Схема замещения диода

Эквивалентная схема всей цепи представлена на рис.71.

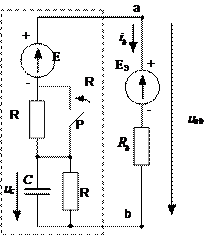
Для схемы замещения:

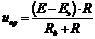, (101)

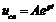, (102)

где А – постоянная интегрирования;

p – корень характеристического уравнения.

Переходная функция напряжения на конденсаторе:

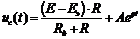. (103)

Рис.71. Эквивалентная цепь

Составим характеристическое уравнение для эквивалентной цепи:

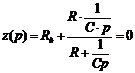, (104)

откуда: 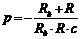. (105)

Определим постоянную интегрирования из начальных условий. При 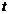=0, напряжение на конденсаторе:

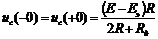. (106)

Подставляя значение для переходной функции (100), получим:

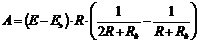. (107)

В итоге переходная функция напряжения на конденсаторе:

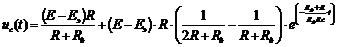. (108)

ЗАДАЧНИК

Нелинейные элементы и их характеристики

Характеристики большинства реальных элементов в той или иной степени нелинейны. В одних случаях нелинейность элементов невелика и при построении упрощенной модели ею можно пренебречь, в других – нелинейностью пренебречь нельзя. Более того, функционирование большинства радиоэлектронных устройств, невозможно без нелинейных элементов (выпрямление, умножение, ограничение, генерирование и т.д.).

Реальные нелинейные элементы подразделяются на безинерционныеи инерционные. Если зависимость между мгновенными значениями тока и напряжения элементов при периодическом воздействии определяется статической вольт - амперной характеристикой (ВАХ), то элемент относится к безинерционнымнелинейным элементам. Если статическая ВАХ и динамическая, снятая при частоте, равной или меньшей рабочей, не совпадают, то такой элемент следует рассматривать какинерционный.

Таким образом, инерционный нелинейный элемент является линейным относительно мгновенных значений тока и напряжения, а ВАХ, связывающая действующие значения 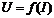оказывается нелинейной. Безинерционные элементы являются нелинейными как в отношении мгновенных значений 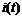, , 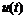так и в отношении действующих 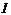и .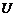

В зависимости от числа внешних выводов различают нелинейные элементы двухполюсные (диоды, термисторы) имногополюсные (транзисторы, триоды, пентоды). Вольт - амперная характеристика нелинейного двухполюсного элемента может быть симметричной или несимметричной. ВАХ двухполюсника с симметричной характеристикой представлена на рис.1. Для нее выполняется условие:

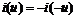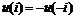, . (1)

Очевидно, что режим работы нелинейной цепи не изменится, если выводы нелинейного элемента с симметричной характеристикой поменять местами. Если условие (1) не выполняется, ВАХ – несимметрична.

Отношение напряжения, измеряемого отрезком АВ к току, измеряемому отрезком ОВ (см.рис.1.), определяет в некотором масштабе 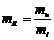статическое сопротивление R в точке А.

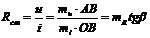(2)

Предел отношения приращения напряжения на участке цепи к приращению тока в нем или производная от напряжения по току в том же масштабе 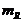, определяет дифференциальное сопротивление:

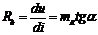. (3)

Различают нелинейные элементы с монотоннойи немонотоннойВАХ. Для монотонныхВАХ 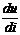или 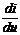всегда больше нуля.

Немонотонные характеристики разделяются на N-и S-типы. У элементов с N-образной характеристикой (рис. 2.а) одному и тому же значению тока может соответствовать несколько различных напряжений. У S-образнойВАХ одному значению напряжения может соответствовать несколько токов (рис. 2.б).

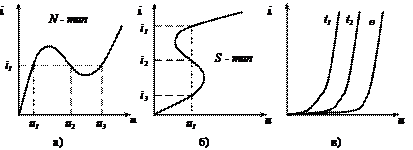
Рис.2. ВАХ различных нелинейных элементов

а) немонотонная N-типа; б) немонотонная S – типа;

в) ВАХ неэлектрически управляемого двухполюсника - термистора.

Вид ВАХ нелинейного элемента может зависеть от некоторой величины, не связанной с токами и напряжениями цепи, в которую включен элемент, в частности от температуры (рис. 2.в), освещенности, давления и т.д. Такие элементы относятся кнеэлектрически управляемым двухполюсникам.

Рис.3. Электрически управляемый элемент

а) транзистор; б) семейство входных ВАХ;

в) семейство выходных ВАХ.

Важнейший класс нелинейных элементов составляют электрическиуправляемые элементы(транзисторы, тиристоры, и т.д.). Они имеют два основных электрода и один управляющий (рис.3.а). Ток 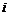элемента определяется уравнениями:

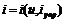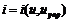или . (4)

Выводы нелинейного управляемого трёхполюсника образуют с остальной частью цепи два контура – основной (выходной) и управляющий (входной).

Управляемые элементы характеризуются семействами ВАХ: выходными и входными. (рис.3.б,с)

Вид ВАХ нелинейного управляемого элемента существенно зависит от схемы включения элемента, т.е. от того какой из электродов является общим для основного и управляющего контуров. На принципиальных электрических схемах реальные нелинейные элементы изображаются с помощью установленных ЕСКД условных графических обозначений (рис.4).

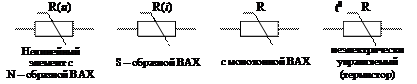
Рис.4 Обозначения нелинейных элементов