Деление отрезка в данном отношении
Пусть даны точки 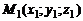 и
и 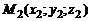 . Требу-ется найти координаты точки
. Требу-ется найти координаты точки 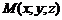 , делящей отрезок прямой, заключенный между М1 и М2, в отношении
, делящей отрезок прямой, заключенный между М1 и М2, в отношении 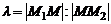 ,
, 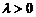 (рис. 7.6).
(рис. 7.6).

Рис. 7.6
Рассмотрим векторы
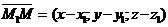 и
и 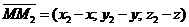 . Они коллинеарны и одинаково направлены, то есть могут отли-чаться только длиной. По условию
. Они коллинеарны и одинаково направлены, то есть могут отли-чаться только длиной. По условию
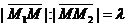 ,
,
поэтому
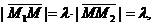
или в координатной форме
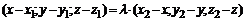 .
.
Из равенства этих двух векторов следует равенство их соот-ветствующих координат:
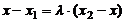 ,
, 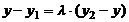 ,
, 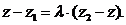
Отсюда
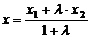 ,
, 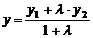 ,
, 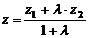 ,
, 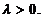
В частности, если точка М делит отрезок М1М2 пополам, то 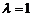 и
и 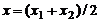 ,
, 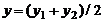 ,
, 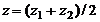 , то есть координаты точки, делящей отрезок пополам, равны полусуммам соответствующих координат концов отрезка.
, то есть координаты точки, делящей отрезок пополам, равны полусуммам соответствующих координат концов отрезка.
Пример 7.12.Найти координаты точки М, делящей по-полам отрезок прямой 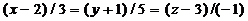 , заключенный между плоскостями Oxz и Оxу.
, заключенный между плоскостями Oxz и Оxу.
Решение. Найдем точку пересечения прямой с плоскостью Oxz, полагая в уравнениях прямой 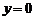 . Тогда получим
. Тогда получим
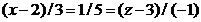
или
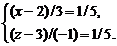
Из последней системы находим 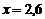 ,
, 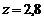 . Эти коор-динаты вместе с
. Эти коор-динаты вместе с 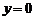 определяют точку
определяют точку 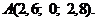 Анало-гично, полагая в уравнениях прямой
Анало-гично, полагая в уравнениях прямой 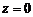 , имеем:
, имеем: 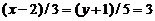 или
или 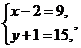 откуда
откуда 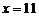 ,
, 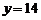 . Получим точку
. Получим точку 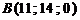 пересечения прямой с плоскостью Оxу. Зная координаты концов
пересечения прямой с плоскостью Оxу. Зная координаты концов 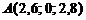 и
и 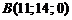 отрезка АВ, по формулам деления отрезка пополам определим координаты точки М – середины отрезка АВ:
отрезка АВ, по формулам деления отрезка пополам определим координаты точки М – середины отрезка АВ: 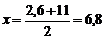 ;
; 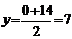 ;
; 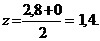 Итак,
Итак, 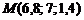 – искомая точка.
– искомая точка.
Пример 7.13. Даны координаты вершин пирамиды 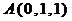 ,
, 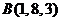 ,
, 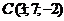 ,
, 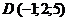 . Найти: 1) длины ребер АВ и AC; 2) угол между ребрами АВ и АС; 3) площадь грани АВС; 4) объем пирамиды ABCD; 5) уравнение прямой АВ; 6) уравнение плоскости АВС; 7) уравнение высоты пирамиды, опущенной на грань АВС. Сделать чертеж.
. Найти: 1) длины ребер АВ и AC; 2) угол между ребрами АВ и АС; 3) площадь грани АВС; 4) объем пирамиды ABCD; 5) уравнение прямой АВ; 6) уравнение плоскости АВС; 7) уравнение высоты пирамиды, опущенной на грань АВС. Сделать чертеж.
Решение
1)Длина ребра AB совпадает с длиной вектора 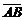 , поэтому определим координаты векторов
, поэтому определим координаты векторов 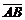 и
и 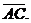
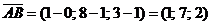 ,
,
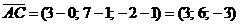 .
.
Длина вектора равна корню квадратному из суммы квадратов его координат, то есть
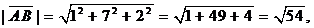
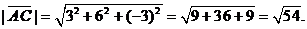
2)Угол между ребрами AB и AC совпадает с углом между векторами 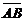 и
и 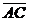 , который можно определить по формуле:
, который можно определить по формуле:
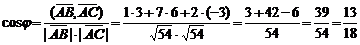 ,
, 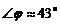 .
.
3)Грань ABC представляет собой треугольник, его пло-щадь найдем через векторное произведение:
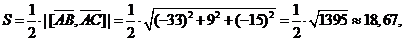
так как
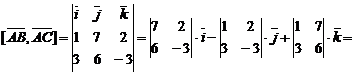
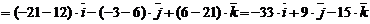 .
.
4)Объем пирамиды вычислим по формуле:
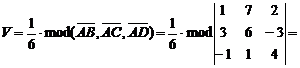
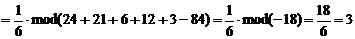 .
.
Здесь 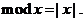
5)Уравнение прямой, проходящей через точки А, В, имеет вид:
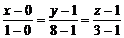 , то есть
, то есть 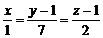 .
.
6)Уравнение плоскости ABC определим из равенства
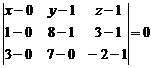 ,
, 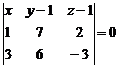 или
или
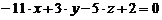 .
.
7)Так как высота – это прямая, перпендикулярная плос-кости ABC, ее направляющим вектором будет вектор-нормаль 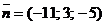 плоскости ABC, тогда уравнение высоты имеет вид:
плоскости ABC, тогда уравнение высоты имеет вид:
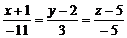 .
.
Выполним чертеж (рис. 7.5).
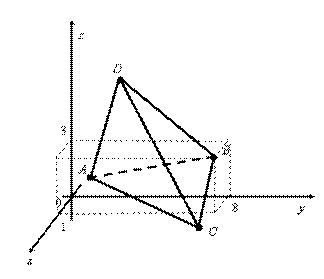
Рис. 7.5
ТЕМА 8. Функции. Теория пределов
Понятие функции
В теме 5 мы уже встречались с понятием функции, информация о которой основывалась на материале из школьного курса математики. Здесь это понятие получит свое дальнейшее развитие.
Пусть на действительной оси R заданы два числовых множества 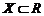 и
и 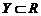 .
.
Определение. Будем говорить, что на множестве X задана функция f действительной переменной x, если известен закон (отображение), по которому каждому значению 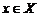 по закону f ставится в соответствие единственное значение
по закону f ставится в соответствие единственное значение 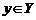 и обозначается
и обозначается  . Переменная x называется аргументом функции f, множество X – областью определения функции, переменная y – значением функции или зависимой переменной, а множество Y – областью значений функции.
. Переменная x называется аргументом функции f, множество X – областью определения функции, переменная y – значением функции или зависимой переменной, а множество Y – областью значений функции.
Замечание. Область Y значений функции обычно не указыва-ется, так как множество принимаемых значений функции определяет сам закон.
Допускаются многозначные функции (то есть одному x соответствует более одного значения y). Обычно эти случаи оговариваются особо.
Замечание. Для обозначения функциональной зависимос-ти вместо символа функции f можно использовать любую дру-гую букву (но не число) любого алфавита.
Определение. Совокупность всех значений независимой переменной х, для которых функция  определена, назы-вается областью определения, или областью существования функции, и обозначается
определена, назы-вается областью определения, или областью существования функции, и обозначается 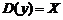 .
.
Определение. Пусть задана функция  . Тогда
. Тогда 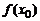 называется значением этой функции при
называется значением этой функции при 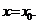
Пример 8.1. Найти значения 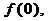
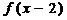 функции
функции 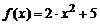 .
.
Решение. Вычислим значения функции при заданных значениях аргумента 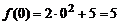 ;
; 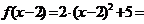
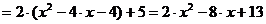 .
.
Способы задания функции
Чтобы задать функцию  , необходимо указать правило, позволяющее по известному значению x находить соответствующее значение y.
, необходимо указать правило, позволяющее по известному значению x находить соответствующее значение y.
Наиболее популярные следующие способы задания функции.
1) Табличный. При табличном задании просто выписы-вается ряд значений независимой переменной и соответствую-щие им значения функции.
Табличный способ задания функций особенно распространен в естествознании и технике. Например, при изучении зависимости электрического сопротивления r некоторого медного стержня от тем-пературы t была получена следующая таблица:
| t | 19,1 | 25,0 | 30,1 | 36,0 | 40,0 | 45,1 | 50,0 |
| r | 76,30 | 77,80 | 79,75 | 80,80 | 82,35 | 83,90 | 85,10 |
2) Аналитический. Аналитическое задание функции сос-тоит в том, что дается формула, с помощью которой по задан-ным значениям независимой переменной можно получать соот-ветствующие им значения функции.
Например, 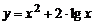 или
или 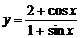 – формулы, которые определяют y как функцию от х.
– формулы, которые определяют y как функцию от х.
В свою очередь аналитическое задание функции бывает явное, неявное, параметрическое и др.
Определение. Функция, заданная формулой (аналитически) вида  , то есть разрешенной относительно зависимой переменной, называется явной.
, то есть разрешенной относительно зависимой переменной, называется явной.
Рассмотрим функцию 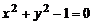 . Здесь y однозначно не выражается через x, это неявная функция. Графиком этой функции является окружность с центром в точке
. Здесь y однозначно не выражается через x, это неявная функция. Графиком этой функции является окружность с центром в точке 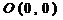 и радиусом
и радиусом 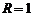 .
.
Определение. Функция, заданная уравнением 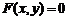 , не разрешенным относительно зависимой переменной, называется неявной функцией.
, не разрешенным относительно зависимой переменной, называется неявной функцией.
Неявная функция может быть как однозначной, так и многозначной. Например, функция 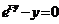 является однозначной неявной функцией.
является однозначной неявной функцией.
Для доказательства существования неявной функции 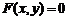 следует доказать, что существует решение этого уравнения, то есть найти функцию
следует доказать, что существует решение этого уравнения, то есть найти функцию 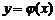 , такую, что вы-полняется равенство
, такую, что вы-полняется равенство 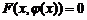 ,
, 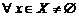 .
.
Определение. Функция задана параметрически, если соответствующие значения x и y выражены через третью переменную t, называемую параметром, то есть 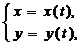
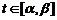 .
.
Например, 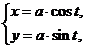
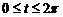 –уравнение окружности радиуса а.
–уравнение окружности радиуса а.
3) Графический
Определение. Графиком функции называется множество всех точек 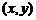 плоскости, абсциссы которых являются значениями независимой переменной х, а ординаты – соответствующими значениями функции
плоскости, абсциссы которых являются значениями независимой переменной х, а ординаты – соответствующими значениями функции 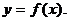 Равенство
Равенство  называется уравнением этого графика [3].
называется уравнением этого графика [3].
Функция задана графически, если начерчен ее график.
Если график функции построен (рис. 8.1), то, чтобы найти значение функции  , отвечающее какому-нибудь зна-чению
, отвечающее какому-нибудь зна-чению 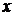 , необходимо отложить это значение
, необходимо отложить это значение 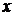 по оси абсцисс и из полученной точки восстановить перпендикуляр до пересе-чения с графиком функции. Длина этого перпендикуляра, взятая с надлежащим знаком, и равна значению функции
по оси абсцисс и из полученной точки восстановить перпендикуляр до пересе-чения с графиком функции. Длина этого перпендикуляра, взятая с надлежащим знаком, и равна значению функции 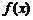 . Например,
. Например, 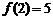 .
.
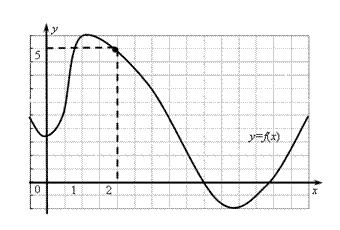
Рис. 8.1
4) Содержательный. При таком способе задания варианты независимой переменной, функции и ее значения формулируются в виде правил, законов и т. д. Например, конституция, УК и т. п.
Замечание. Представленные способы задания имеют свои достоинства и недостатки. К недостаткам табличного способа задания относится то, что, зная таблицу значений функций, не всегда можно найти аналитическое уравнение функции и соответственно значения функции в точках, не представленных в таблице. Наглядность графического способа задания оказывается неоспо-римым плюсом, к недостаткам относится неточность определяемых значений функции. Абсолютно точным способом задания функции является аналитический, так как если известно уравнение (правило) функции, то для любого возможного x всегда найдется значение y. Самый общий способ задания функции – содержательный, однако он чаще используется в гуманитарных дисциплинах и реже в математике, например, в теории вероятностей.
Элементарные функции
Определение. Функции, построенные из простейших эле-ментарных функций и постоянных при помощи конечного чис-ла арифметических действий и конечного числа операций взя-тия функции от функции, называются элементарными.
Простейшими считаются функции:
1)степенная 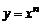 ,
, 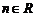 ;
;
2)показательная 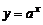 , а>0, а¹1;
, а>0, а¹1;
3)логарифмическая 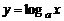 , а>0, а¹1,
, а>0, а¹1, 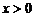 ;
;
4)тригонометрические: 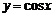 ,
, 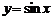 ,
, 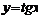 ,
, 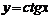 ;
;
5)обратные тригонометрические:  ,
, 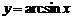 ,
, 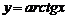 ,
, 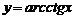 .
.
Примером неэлементарной функции является 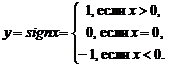
Пусть у является функцией от u, 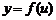 , uÎU, а u – функцией от х,
, uÎU, а u – функцией от х, 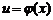 , x Î X, тогда у называется сложной функцией, то есть
, x Î X, тогда у называется сложной функцией, то есть 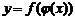 , определенной для тех x Î X, для которых значения
, определенной для тех x Î X, для которых значения 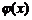 входят во множество U.
входят во множество U.
Например,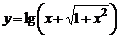 ;
; 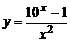 – сложные функции.
– сложные функции.
Пусть функция  определена на симметричном интервале относительно начала координат, то есть
определена на симметричном интервале относительно начала координат, то есть 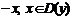 .
.
Определение. Функция  называется четной, если она не изменяет свое значение при изменении знака аргумента, т. е.
называется четной, если она не изменяет свое значение при изменении знака аргумента, т. е. 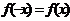 . Функция
. Функция 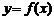 называется нечетной, если при изменении знака аргумента знак функции меняется, то есть
называется нечетной, если при изменении знака аргумента знак функции меняется, то есть 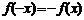 .
.
Замечание. Отметим, что график четной функции симметри-чен относительно оси Оу, а нечетной – относительно начала координат.
Определение. Функция  ,
, 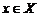 , называется периодичес-кой, если существует число
, называется периодичес-кой, если существует число 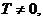 такое, что
такое, что 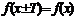 ,
, 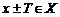 . Наименьшее число T называется периодом (основным периодом).
. Наименьшее число T называется периодом (основным периодом).
Задание функций в полярной системе координат
Зададим на плоскости точку O, которую назовем полюсом. Проведем из полюса направленную полупрямую, которую назо-вем полярной осью.
Пусть M – произвольная точка плоскости. Соединим точку M с полюсом. Длина отрезка OM равна r и называется полярным радиусом, а угол j, откладываемый от полярной оси к отрезку OM против движения часовой стрелки, – полярным углом (рис. 8.2).
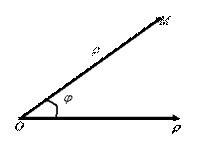
Рис. 8.2
Таким образом, положение точки М на плоскости опреде-ляется двумя координатами r и j, причем r – всегда величина неотрицательная, а угол j может принимать значения от 0 до 2π, то есть 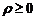 ,
, 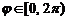 .
.
