Абсолютная и условная сходимости
Для знакопеременных рядов (в частности для знакочередующихся рядов) различают два вида сходимости: абсолютную и условную.
Знакопеременный ряд называется абсолютно сходящимся, если:
-он сходится сам,
-сходится ряд, состоящий из модулей его членов.
Знакопеременный ряд называется условно (неабсолютно) сходящимся, если:
-он сходится сам.
-ряд, состоящий из модулей его членов, расходится.
Эти два типа сходимости можно распространять на любые числовые ряды, а не только на знакопеременные, так как для знакоположительных рядов их сходимость очевидно совпадает с абсолютной сходимостью.
Примеры:
Исследуем следующие ряды на абсолютную или условную сходимости:
1) 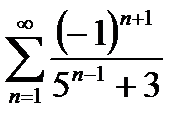
данный ряд является знакочередующимся; имея в виду набор достаточных признаков для ряда этого типа, целесообразно начать исследование ряда, составленного из модулей членов данного ряда:
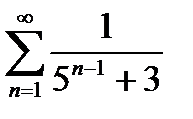 - знакоположительный ряд, он сходится по признаку сравнения в непредельной форме, так как
- знакоположительный ряд, он сходится по признаку сравнения в непредельной форме, так как 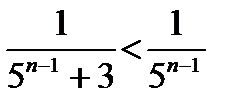 и ряд
и ряд 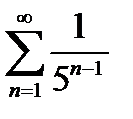 является сходящимся;
является сходящимся;
Следовательно, по признаку абсолютной сходимости исходный знакочередующийся ряд тоже сходится.
Таким образом, для данного ряда выполнены требования абсолютной сходимости, поэтому ряд 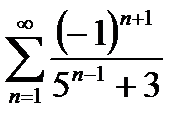 сходится абсолютно.
сходится абсолютно.
2) 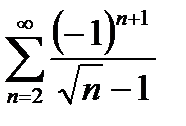 - знакочередующийся ряд.
- знакочередующийся ряд.
его ряд из модулей 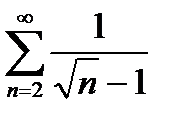 расходится по признаку сравнения в непредельной форме, так как
расходится по признаку сравнения в непредельной форме, так как
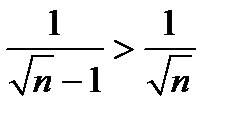 и ряд
и ряд 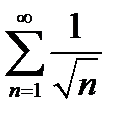 расходится;
расходится;
следовательно, признак абсолютной сходимости не дает ответа для исходного знакочередующегося ряда
На основании этого исследования делаем вывод, что для исходного ряда абсолютной сходимости нет, остается проверить условную сходимость, применив признак Лейбница к знакочередующемуся ряду:
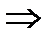 исходный знакочередующийся ряд сходится по признаку Лейбница.
исходный знакочередующийся ряд сходится по признаку Лейбница.
Таким образом, получили, что данный знакочередующийся ряд сходится, но ряд из его модулей расходится. Поэтому этот ряд 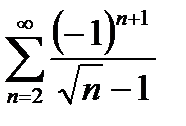 сходится условно.
сходится условно.
3) 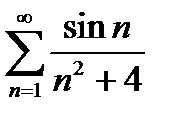 - знакопеременный ряд;
- знакопеременный ряд;
исследуем сходимость соответствующего ряда из модулей:
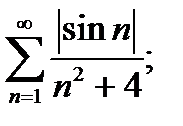
этот знакоположительный ряд сходится по признаку сравнения, так как
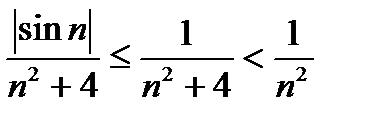 и ряд
и ряд 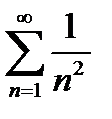 сходящийся;
сходящийся;
по признаку абсолютной сходимости заключаем, что исходный ряд так же является сходящимся.
На основании определения абсолютной сходимости делаем вывод, что знакопеременный ряд 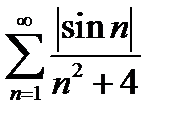 сходится абсолютно.
сходится абсолютно.
Упражнения для самостоятельной работы
Задача 1
Исследуйте на сходимость следующие знакопеременные ряды, используя достаточный признак абсолютной сходимости:
1) 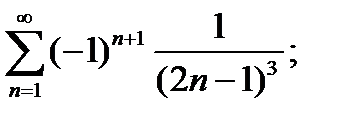 2)
2) 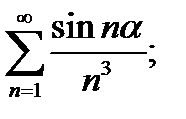 3)
3) 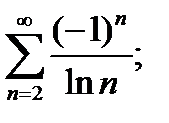 4)
4) 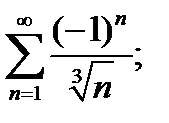
5) 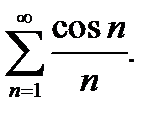
Задача 2
Исследуйте на сходимость для следующих знакочередующиеся ряды по признаку Лейбница:
1) 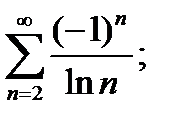 2)
2) 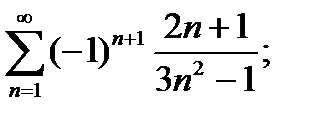 3)
3) 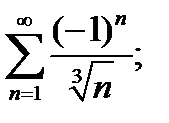 4)
4) 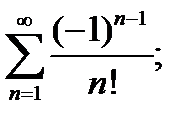 5)
5) 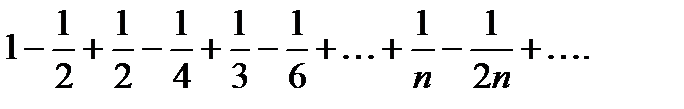
Задача3
Исследуйте тип сходимости (абсолютная или условная) для следующих знакопеременных рядов:
1) 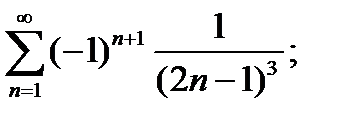 2)
2) 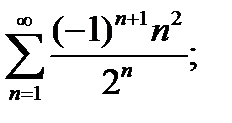 3)
3) 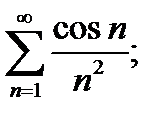
4) 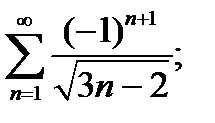 5)
5) 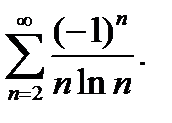
Ответы к упражнениям для самостоятельной работы
Задача 1
1) и 2) – сходятся; 3),4),5) – ответ дать нельзя.
Задача 2
1), 2), 3), 4) – сходятся; 5) – ответ дать нельзя.
Задача 3
1), 2), 3) – сходятся абсолютно; 4),5) – сходятся условно.
