Структура и особенности временных рядов

Временные ряды

Предварительный анализ исходных ВР

Выявление и устранение аномальных наблюдений

Одна из главных задач предварительного анализа заключается в выявлении и устранении аномальных значений уровней ряда. Под аномальным уровнем понимается отдельное значение уровня ВР, которое не отвечает потенциальным возможностям исследуемой экономической системы и которое, оставаясь в качестве уровня ряда, оказывает существенное влияние на значения основных характеристик ВР, в том числе на соответствующую трендовую модель.

Причинами аномальных наблюдений могут быть ошибки технического порядка (ошибки первого рода), которые подлежат выявлению и устранению, и ошибки из-за факторов, имеющих объективный характер, но проявляющихся эпизодически (ошибки второго рода), которые устранению не подлежат.

Основным методом для выявления аномальных уровней ВР является метод Ирвина.

1.Рассчитывают значения λ_t

где – среднее квадратическое отклонение;

– среднее значение (математическое ожидание).

2. Расчетные значения λ₂, λ₃ и т.д. сравнивают с табличными значениями критерия Ирвина λ_α, и если они оказываются больше табличных, то соответствующее значение y_t уровня ряда считается аномальным.

– аномально,

– нормально.

В том случае, когда значение числа уровней n находится в промежутке указанном в таблице, приближенное значение λ_αнаходят графически.

Пример 7.1. Найти приближенное значение λ_α для n=7.

Число n=7 заключено между табличными значениями n=3 и n=10. Графически показываем на плоскости λ_αО_n точки с координатами (n=3, λ_α=2,3) и (n=10, λ_α=1,5) и соединяем их прямой (рис. 7.1).

n

Рис. 7.1. Приближенное определение значения λ_α

Из оси абсцисс О_n восстанавливаем перпендикуляр до пересечения с прямой. Откуда получаем, что λ_α 1,9.

Значение критерия Ирвина при уровне значимости α=0,05 (5%-я ошибка) приведены в таблице

Таблица 7.1

Нормированные значения критерия Ирвина (α=0,05)

n
λα	2,8	2,3	1,5	1,3	1,2	1,1	1,0

3. Устанавливают причины появления аномальных уровней ряда. Если они вызваны ошибками первого ряда, то они устраняются либо заменой аномальных уровней средней арифметической двух соседних уровней ряда, либо заменой аномальных уровней соответствующими значениями по кривой, аппроксимирующей данный ВР.

Таблица 7.2

Табулированные значения μ, σ₁, σ₂

n
μ	3,858	5,195	5,990	6,557
σ1	1,288	1,677	1,882	2,019
σ2	1,964	2,279	2,447	2,561

г) сравниваются расчетные значения t_s и t_d с табличными t_α с заданным уровнем значимости; если t_s<t_α и t_d<t_α , то тренды в среднем и у дисперсии отсутствуют; если t_s>t_α и t_d<t_α , то имеется тренд в среднем, а тренда у дисперсии ряда – нет и т.д.; t-критерий Стьюдента выбирается из условия α и (n–1).

Методы сглаживания ВР

Очень часто уровни экономических рядов динамики колеблются и тенденция развития экономического явления во времени скрыта случайными отклонениями уровней в ту или иную сторону. Чтобы более четко обозначить тенденцию развития процесса, производят сглаживание (выравнивание) ВР.

Различают аналитическое выравнивание с помощью известных уравнений различных линий (прямая, экспонента и.т.д.) и механическое выравнивание ВР с использованием фактических значений соседних уровней.

При механическом сглаживании берется несколько первых уровней ВР (интервал сглаживания). Для них подбирается полином, степень которого должна быть меньше числа уровней, входящих в интервал сглаживания. С помощью полинома определяются новые, выровненные значения уровней в середине интервала сглаживания. Далее интервал сглаживания сдвигается на один уровень ряда вправо и вычисляется второе сглаженное значение и.т.д.

Метод простой скользящий средней. Интервал по возможности берут большим и состоящим из нечетного числа уровней. Для первых m уровней, образующих интервал сглаживания, вычисляют среднее арифметическое значение, которое соответствует середине интервала:

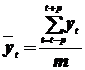; t > p; 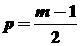(m – нечетно).

Далее делается сдвиг на один уровень вправо и операция повторяется.

В результате такой процедуры получаются n–m+1 сглаженных значений уровней ряда. При этом первые и последующие p уровней теряются (не сглаживаются). Рекомендуется только для рядов, имеющих линейную тенденцию.

В методе взвешенной скользящей средней уровни, входящие в интервал сглаживания, суммируются с разными весами, т.к. для сглаживания используются полиномы второй и большей степени.

Средняя арифметическая взвешенная определяется как:

,

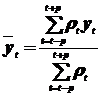где ρ_t – веса, определяемые методом наименьших квадратов.

Особенностью метода экспоненциального сглаживания является то, что в процедуре нахождения сглаженного уровня используются значения только предшествующих уровней ряда, взятые с определенным весом, причем вес наблюдения уменьшается по мере удаления его от момента времени, для которого определяется сглаженное значение уровня ряда.

Сглаженные значения уровней S_t , t=1,2,…,n определяются по формуле:

S_t = αy_t + (1–α)S_t-1,

где α – параметр сглаживания (0<α<1);

(1–α) – коэффициент дисконтирования.

Сглаженное данным методом значение уровня ряда является взвешенной средней всех предшествующих уровней:

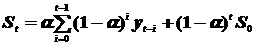
где S₀ – величина, характеризующая начальные условия; рекомендуются выбирать S₀=y₁ или S₀=1/3(y₁+y₂+y₃).

Значение α рекомендуется выбирать в пределах 0,1 0,3. Р.Браун предлагает выбирать α, исходя из данных ряда:

.

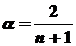Если при подходе к правому концу ВР, сглаженные этим методом значения при выбранном параметре α начинают значительно отличаться от соответствующих значений исходного ряда, то необходимо перейти на другой параметр сглаживания.

При этом методе не теряются ни конечные, ни начальные уровни ВР.

Оценка автокорреляции во ВР

Часто возникает необходимость оценить зависимость изучаемого показателя y_t от его значений, рассматриваемых с некоторым запаздыванием во времени. Зависимость значений уровней ВР от предыдущих (сдвиг на 1), предпредыдущих (сдвиг на 2) и.т.д. уровней того же ВР называется автокорреляцией во ВР.

Автокорреляционная функция вычисляет взаимную корреляционную функцию между исходным рядом y_t и этим же рядом, сдвинутым во времени на величину τ.

.

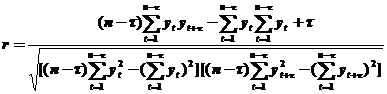Задавая различные значения τ=1,2,3,… (сдвиг) получают значения r₁, r₂, r₃,… и т.д. На практике рекомендуется вычислять такие коэффициенты в количестве от n/4 до n/3.

График автокорреляционной функции называется кореллограммом и показывает величину запаздывания, с которым изменение показателя y_t сказывается на его последующих значениях. Величина сдвига τ, которому соответствует наибольший коэффициент автокорреляции, называется временным лагом.

Иногда используется упрощенная формула:

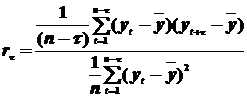
где 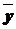– средний уровень ряда.

Пример 7.2. Найти коэффициент автокорреляции r_τ ВР для разных значений лага на основании 10-ти наблюдений, представленных стационарным рядом:

y_t = (421;392;403;350;364;406;418;382;318;354).

Определяем среднее арифметическое членов ВР:

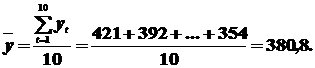
Подсчитывая значение коэффициента автокорреляции для следующих значений лага τ=1,2,…,5. Для этого составим таблицу.

Таблица 7.3

Рис. 7.2. График автокорреляции ВР

что коэффициент автокорреляции имеет колебательный затухающий характер. Это говорит о том, что по мере удаления от данной точки t стохастическая связь между значениями членов ВР уменьшается.

Кривые роста и их выбор

Плавную кривую (гладкую функцию), аппроксимирующую ВР, принято называть кривой роста. Использование метода экстраполяции на основе кривых роста для прогнозирования базируется на двух предположениях:

- ВР экономического показателя действительно имеет тренд;

- общие условия, определяющие развитие показателя в прошлом, останутся без существенных изменений в течении периода упреждения.

Известно большое количество типов кривых роста для экономических процессов.

Таблица 7.4

Выбор вида кривой роста

Показатель	Характер изменения показателя во времени	Вид кривой роста
Первый средний прирост	Примерно одинаковы	Полином первого порядка (прямая)
Первый средний прирост	Изменяются линейно	Полином второго порядка (парабола)
Второй средний прирост	Изменяются линейно	Полином третьего порядка (кубическая парабола)
	Примерно одинаковы	Простая экспонента
	Изменяются линейно	Модифицированная экспонента
	Изменяются линейно	Кривая Гомперца
	Изменяются линейно	Логистическая кривая

Таблица 7.5

Исходные данные задачи

№ п/п=k
t
yk	7,4	8,4	9,1	9,4	9,5	9,5	9,4

Составим расчетную таблицу (таблица 7.6) для системы уравнений.

Таблица 7.6

Расчетная таблица задачи

№ п/п=k	tk	tk2	tk3	tk4	yk	tk ּ yk	tk2 ּ yk
					7,4	51,8	362,6
					8,4	67,2	537,6
					9,1	81,9	737,1
					9,4	94,0	940,0
					9,5	104,5	1149,5
					9,5	114,0	1368,0
					9,4	122,2	1588,6
∑					62,7	635,6	6683,4

Получаем систему уравнений:

Решая систему, получаем a₀ = 2,12; a₁ = 1,10; a₂ = - 0,04.

Тогда

Для нахождения параметров экспоненциальных и S-образных кривых их сначала логарифмируют, чтобы получить линейное выражение относительно логарифмов, а затем используют метод наименьших квадратов.

При определении параметров кривых роста, имеющих асимптоты, различают два случая. Если значение асимптоты известно заранее, то перенося значение параметра к и логарифмируя, получают полином относительно логарифмов, а затем используют метод наименьших квадратов.

Если значение асимптоты неизвестно, то используют приближённые методы: метод трёх точек, метод трёх сумм и т.д.

Проверка качества моделей

Адекватность модели

Для проверки адекватности модели исследуют ряд остатков

,

т.е. отклонений расчетных значений от фактических . Если трендовая модель выбрана правильно, то для остатков ха­рактерно: равенство нулю математического ожидания; случай­ный характер отклонений от математического ожидания; отсут­ствие автокорреляции и неизменность дисперсии остатков во времени; нормальный закон распределения. Рассмотрим пере­численные требования подробнее.

1. Проверка равенства математического ожидания уровней ряда остатков нулю осуществляется на основе t-критерия Стьюдента. Вычисляется расчетное t_p значение этого критерия:

(7.1)

где – среднее арифметическое значение уровней ряда остатков;

– среднеквадратическое отклонение для последовательности ε_t.

(7.2)

Расчетное значение критерия t_p сравнивается с табличным t_α,ν. На уровне значимости α гипотеза отклоняется, если t_p>t_α,ν, где t_α,ν– критерий распределения Стьюдента с довери­тельной вероятностью (1 – α) и ν = n - 1 степенями свободы.

2. Для проверки условия случайности возникновений отдельных отклонений от трендачасто используется критерий пиков, основанный на поворотных точках. Значение случайной переменной считается поворотной точкой, если оно одновременно боль­ше соседних с ним элементов или, наоборот, меньше значений предыдущего и последующего за ним элементов.

В случай­ной выборке среднее арифметическое числа поворотных точек равна = 2 / 3 (n – 2),

а их дисперсия вычисляется по формуле:

.

Учитывая эти соот­ношения, критерий случайности отклонений от тренда при уров­не вероятности 0,95 можно представить, как

(7.3)

,

где р – фактическое количество поворотных точек в случайном ряду, а квадратные скобки означают, что от результата вычисле­ния следует взять только целую часть, отбросив дробную, какой бы она не была.

Если неравенство не соблюдается, то ряд остатков нельзя считать случайным (т.е. он содержит регулярную компоненту), и стало быть, модель не является адекватной.

3. Наличие (отсутствие) автокорреляции в отклонениях от модели роста проще всего проверить с помощью критерия Дарбина-Уотсона. С этой целью строится (d критерий) Дарбина-Уотсона, в основе которого лежит расчетная формула

(7.4)

Теоретическое основание применения этого критерия обус­ловлено тем, что в динамических рядах как сами наблюдения, так и отклонения от них распределяются в хронологическом порядке.

При отсутствии автокорреляции значение dпримерно рав­но 2, а при полной автокорреляции — 0 или 4. Следовательно, оценки, получаемые по критерию, являются не точечными, а интервальными. Верхние (d₂) и нижние (d₁) критические значе­ния, позволяющие принять или отвергнуть гипотезу об отсут­ствии автокорреляции, зависят от количества уровней временного ряда и числа независимых переменных модели. Значе­ния этих границ для уровня значимости α = 0,05 даны в таблице 7.7, где k – число независимых переменных.

Таблица 7.7

Точность модели

Оценка точности модели имеет смысл только для адекват­ных моделей. В случае ВР точность модели опре­деляется как разность между фактическим и расчетным значени­ями. В качестве статистических показателей точности чаще все­го применяют стандартную ошибку прогнозируемого показателя, или стандартное среднеквадратическое отклонение от линии тренда

(7.6)

где m – число параметров модели, и среднюю относительную ошибку аппроксимации

(7.7)

Если ошибка, вычисленная по последней формуле, не превос­ходит 15%, точность модели считается приемлемой. В общем случае допустимый уровень точности, а значит и надежности, устанавливает пользователь модели, который в результате содер­жательного анализа проблемы выясняет, насколько она чувстви­тельна к точности решения и насколько велики потери из-за неточного решения.

Пример расчета ВР и прогноза по этому ряду

Рассмотрим разработку трендовой модели и получение прогнозных оценок динамики изменения параметра на основе временного ряда, представленного в таблице 7.8.

Таблица 7.8

Исходные данные ВР

t	Параметр
	419,08
	379,8
	410,7

Простой анализ данных таблицы 7.8 позволяет сделать вывод о том, что значение параметр y_t монотонно возрастает, т.е. имеется положительный тренд, близкий к линейному, т.к. первый средний прирост примерно одинаков (таблица 7.4). Кроме того среди значений параметра y_t нет аномальных. Все вышеизложенное позволяет сразу перейти к выбору модели ВР. Выбираем в качестве кривой роста линейную модели вида:

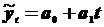
и определяем неизвестные значения коэффициентов а₀ и а₁ по методу наименьших квадратов (§ 7.4).

(7.10)

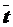Заполним рабочую таблицу 7.9, где в первой нижней строке таблицы записаны суммы соответствующих граф, во второй – соответствующие средние значения и 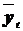. Следуя формулам из метода наименьших квадратов, оценим параметры линейной модели роста: а₀ = 256,36 и а₁ = 14,32. Таким образом, искомая модель принимает вид: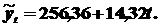

Последовательно подставляя в (7.10) вместо фактора t его значения от 1 до n=14, заполним остальные графы расчётных уровней таблицы 7.9.

Таблица 7.9

Расчетные данные для ВР

t	yt		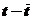		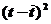		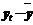	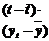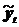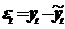Точ. пов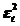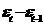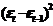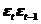
	238,00	-6,5	42,25	-125,76	817,44	270,68	-32,68	-	1067,98	-	-	-
	249,00	-5,5	30,25	-114,76	631,18	285,00	-36,00		1296,00	-3,32	11,02	1176,48
	287,00	-4,5	20,25	-76,76	345,42	299,32	-12,32		151,78	23,68	560,74	443,52
	340,00	-3,5	12,25	-23,76	83,16	313,64	26,36		694,85	38,68	1496,14	-324,76
	342,00	-2,5	6,25	-21,76	54,4	327,96	14,04		197,12	-12,32	151,78	370,09
	373,00	-1,5	2,25	9,24	-13,86	342,28	30,72		943,72	16,68	278,22	431,31
	360,00	-0,5	0,25	-3,76	1,88	356,60	3,40		11,56	-27,32		104,45
	380,00	0,5	0,25	16,24	8,12	370,92	9,08		82,45	5,68	32,26	30,87
	403,00	1,5	2,25	39,24	58,86	385,24	17,76		315,42	8,68	75,34	161,26
	419,10	2,5	6,25	55,34	138,35	399,56	19,54		381,81	1,78	3,16	347,03
	451,00	3,5	12,25	87,24	305,34	413,88	37,12		1377,89	17,58	309,05	725,32
	460,00	4,5	20,25	96,24	433,08	428,20	31,80		1011,24	-5,32	28,30	1180,42
	379,80	5,5	30,25	16,04	88,22	442,52	-62,72		3933,80	-94,52	8934,03	-1994,50
	410,70	6,5	42,25	46,94	305,1 1	456,84	-46,14	-	2128,90	• 16,58	274,89	2893,90
Σ		5092,6		227,50	-0,04	3256,70	5092,64	-0,04		13594,52	-	12901,31	5545,40
ср.	7,5	363,76

Для проверки адекватности модели в соответствии с ви­дом формул (7.1), (7.4) и (7.4а) организуем и заполним графы 9 – 13, и строим график (рис. 7.3).

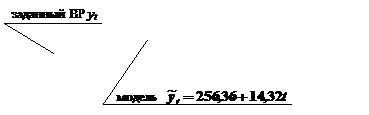
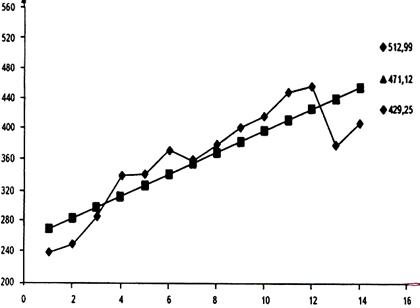
Рис. 7.3. Экспериментальный и теоретический ряды

1. Легко убедиться, что математическое ожидание ряда остатков равно нулю, т.е. | 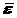| = 0, что следует из суммы 8-ого столбца (-0,04).

2. Проверка случайности ряда остатков по критерию пи­ков дает положительный результат, т.к. р = 7 (9 столбец таблицы 7.9), а критическое число поворотных точек, рассчитанное по формуле (7.3) равно 5. Таким образом, выполняется условие 7>5.

3. При проверке независимости уровней ряда остатков друг от друга значение d = 0,95, вычисленное по формуле (7.4), при уровне значимости α = 0,025 попадает в интервал между d₁ = 0,920 и d₂ = 1,060, т.е. в область неопределенности. Поэтому придется воспользоваться формулой (7.4а): r₁ = 0,41. Сопоставляя это число с табличным значением первого коэффициента ав­токорреляции 0,485, взятым для уровня значимости α = 0,01 и n = 14, увидим, что расчетное значение меньше табличного. Это означает, что с ошибкой в 1% ряд остатков можно считать не­коррелированным, т.е. свойство взаимной независимости уров­ней остаточной компоненты подтверждается.

4. Соответствие ряда остатков нормальному распределению установим с помощью формулы (7.5). Вычислим вари­ационный размах ε_max– ε_max = 99,84 и среднеквадратическое отклонение δ_ε = 32,34. По этим данным рассчитаем критерий R/S=3,09. Для n = 14 и α = 0,05 найдем критическим интервал: [2,92; 4,05]. Вычисленное значение 3,09 попадает между табулированными границами с заданным уровнем вероятности. Значит, закон нормального распределения выполняется, и можно строить до­верительный интервал прогноза.

5. Так как модель оказалась адекватной, оценим ее точность. По формуле (7.7) рассчитаем среднюю относительную ошибку: Е_отн = 7,7%. Такую ошибку можно считать приемлемой, 7,7<15.

6. Экстраполяция уравнения = 256,36 + 14,32t на шаг впе­ред, т.е. на момент времени n + 1 = 15, дает прогнозное значе­ние параметра, равное 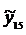= 471,12.

7. Для построения интервального прогноза рассчитаем доверительный интервал (7.9). Примем значение уровня значимости α = 0,3, а значит, доверительную вероятность – 70 %. В этом случае критерий Стьюдента (при v = n –2 = 12) равен t_α,v= 1,083. Вычислив среднеквадратическую ошибку тренда (7.6), с учетом значения t_α,v получим интервальный прогноз (см. рис. 7.3):

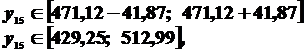
где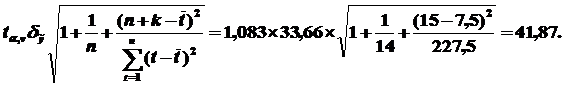

Таким образом, построенная нами модель является полно­стью адекватной динамике параметра и достаточно надежной для крат­косрочных прогнозов. Поэтому с вероятностью 0,7 (70%) можно утверждать, что при сохранении сложившихся закономерностей развития значения параметра y_t, прогнозируемое на t=15 с помощью линейной модели роста, попадет в промежуток, обра­зованный нижней и верхней границей доверительного интервала (429,25; 512,99).

Адаптивное прогнозирование

Адаптивными методами прогнозирования принято назы­вать такие методы, процесс реализации которых заключается в вычислении последовательных во времени значений прогнози­руемого показателя с учетом степени влияния предшествующих уровней. При краткосрочном прогнозировании наиболее важным является не тенденция развития исследуемого процесса, сложив­шаяся в среднем на всем периоде предыстории, а последние зна­чения этого процесса. Свойство динамичности развития эконо­мического явления здесь преобладает над свойством его инерци­онности. Поэтому при краткосрочном прогнозировании, как правило, более эффективными оказываются адаптивные методы, учитывающие неравноценность уровней временного ряда и бы­стро приспосабливающие свою структуру и параметры к изме­няющимся условиям.

Наиболее распространенным из адаптивных методов является метод Брауна, в котором расчетное значение y_р в момент времени t находится по формуле:

y_p (t) = a₀ (t – 1) + a₁ (t – 1)k

где k – количество шагов прогнозирования (обычно k = 1).

Это значение сравнивается с фактическим уровнем, и по­лученная ошибка прогноза

Е (t) = y (t) – y_p(t)

используется для корректировки модели. Корректировка параметров осуществляется по формулам:

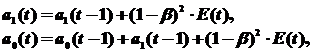
где β– коэффициент дисконтирования данных (уровень значимости), отражающий большую степень доверия к более поздним данным. Его значе­ние должно быть в интервале от 0 до 1. Процесс модификации модели (t = 1, 2, ..., n) в зависи­мости от текущих прогнозных качеств обеспечивает ее адап­тацию к новым закономерностям развития. Для прогнозиро­вания используется модель, полученная на последнем шаге (при t = n).

Воспользуемся схемой адаптивного прогнозирования для примера, рассмотрен­ного в §7.7. Начальные оценки параметров получим по первым пяти значениям y_t при помощи метода наименьших квадратов (рис. 7.4).

y5

y4

y3

y2

y1

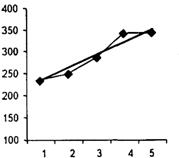
Рис. 7.4. Получение начальных значений параметров a₀ (0) и a₁ (0)

(7.10)

(7.10)

(7.10)

Линейная модель для y₁ – y₅ имеет вид: y = 29,9x + 201,5. Откуда

a₀(0) = 201,5, a₁(0) = 29,9.

Возьмём α = 0,8, k = 1 и β = 1 – α = 0,2 и по формулам адаптирования

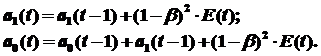
получим скорректированные значения параметров a₀(t) и a₁(t) (таблица 7.10).

Таблица 7.10

Расчет скорректированных значений a₀(t) и a₁(t)

Время	Факт yt	a0	a1	Расчет yt	Отклонение Е(t)
		201,50	29,90
		237,74	34,12	231,40	6,600
		249,91	19,49	271,86	-22,860
		286,30	30,75	269,41	17,592
		339,08	45,44	317,05	22,951
		343,70	18,23	384,52	-42,523
		372,56	25,31	361,93	11,073
		361,51	1,08	397,87	-37,870
		379,30	12,22	362,59	17,409
		402,54	19,56	391,52	11,478
	419,1	419,22	17,64	422,10	-3,005
		450,43	26,69	436,86	14,139
		460,68	15,73	477,12	-17,124
	379,8	383,66	-46,10	476,42	-96,615
	410,7	407,77	0,71	337,56	73,139
				408,48

Прогнозные оценки по модели расчета y_p (t) получаются путем подстановки в нее значения k = 1, а интервальные – по тем же формулам, что и для кривых роста:

y_p (15) = 407,11 + 0,71 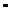1 = 408,48.

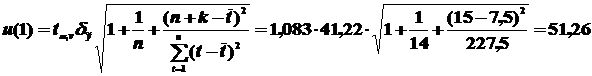k = 1 (t = 15)

Нижняя граница: 408,48 – 51,26 = 357, 21.

Верхняя граница: 408,48 + 51,26 = 459,75.

Сведем все полученные результаты в таблицу (таблица 7.11) и покажем на графике (рис. 7.5).

Таблица 7.11

Рис. 7.5. Результаты аппроксимации и прогнозирования по модели Брауна

При сохранении сложившихся закономерностей дина­мики развития прогнозируемая величина с вероятностью 70% ( t_0,3;12=1,0832 ) попадает в интервал, образованный нижней и верхней границами.

Временные ряды

Структура и особенности временных рядов

Большинство экономических задач связано с оценкой основных экономических показателей во времени и с прогнозом этих показателей на будущие моменты времени. Это значит, что основные экономические характеристики необходимо рассматривать как случайные функции.

Но так как статистика оперирует с выборочными значениями показателей, то из случайных функций производится выборка в дискретные моменты времени. В результате получаются так называемые временные ряды, которые являются частным случаем динамического ряда.

Под временным рядом (ВР) понимается последовательность наблюдений некоторого признака Y в различные, чаще всего равноотстоящие моменты времени.

Если измерения проводятся в равноотстоящие моменты времени, то временной ряд можно представить в виде последовательных значений (уровней) показателя, характеризующего состояние процесса в эти моменты времени

y (1), y (2), ..., y (n) или y₁, y₂,..., y_n,

где n – общее число моментов измерения.

Таким образом, составными элементами ВР являются числовые значения показателя, называемые уровнями этих рядов и моменты или интервалы времени, к которым относятся уровни.

ВР, образованные показателями, которые характеризуют экономическое явление на определенные моменты времени, называются моментными (списочная численность рабочих на первое число каждого месяца). Если уровни ВР образуются путем агрегатирования за определенный промежуток времени, то такие ряды называются интервальными (фонд заработной платы рабочих предприятия по месяцам).

Под длиной ВРпонимают время, прошедшее от начального момента наблюдения до конечного, но иногда длиной ряда называют количество уровней, входящих во ВР.

Следует отметить, что ВР качественно отличаются от простых статистических выборок:

- последовательные по времени уровни ВР являются взаимозависимыми, особенно это относится к близко расположенным наблюдениям;

- в зависимости от момента наблюдения уровня в ВР они обладают разной информативностью: информационная ценность наблюдений убывает по мере их удаления от текущего момента времени;

- с увеличением количества уровней ВР точность статистических характеристик не будет увеличиваться пропорционально числу наблюдений, а при появлении новых закономерностей развития она может даже уменьшаться;

- члены ряда не являются одинаково распределенными, т.е.

P(Y(i) < y) ≠ P(Y(j) < y) при i ≠ j.

Если во ВР