Несколько замечаний о перестановочности членов

Сходящихся – расходящихся рядов.

1) Если ряд сходится абсолютно, то сходится абсолютно и ряд, полученный любой перестановкой членов исходного ряда.

Т°.Пусть дан ряд 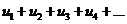(1) с неотрицательными членами, а ряд 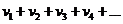(2) получается из него перестановкой его членов. Тогда, если ряд (1) сходится, то ряд (2) также сходится и имеет ту же сумму.

∆ Пусть ряд (1) сходится и его сумма равна S. Рассмотрим частичную умму ряда (2) 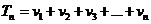. Каждое из слагаемых этой суммы входит в ряд (1). Возьмем в ряде (1) столь большое число m первых членов, чтобы среди них оказались все слагаемые из 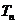, и составим из них m-ю частичную сумму ряда (1): 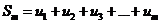. Так как все слагаемые 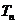входят в 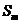, а остальные слагаемые 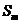(если такие есть) неотрицательны, то 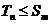. Но частичные суммы ряда (1), ввиду не отрицательности членов ряда, не превосходят его суммы 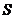: 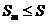и, следовательно, 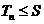. Так как это неравенство для любого n, то все частичные суммы ряда (2) ограничены.

Поэтому ряд (2) сходится и для его суммы Т справедливо .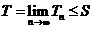

Проводя аналогичные рассуждения не для рядов (1) и (2), а для рядов (2) и (1) получим, что 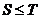. Из двух последних неравенств следует, что ▲

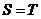2) Члены условно сходящегося ряда (не абсолютно) можно переставлять так, что сумма преобразованного ряда будет равна любому, наперёд заданному элементу числовой прямой.

Изложить идею доказательства и

привести конкретный пример, например с рядом Лейбница

3) Переставить члены условно сходящегося ряда так, чтобы получился ряд сходящийся абсолютно, нельзя.

4) Если знакопостоянный ряд сходится, то он сходится абсолютно и к сумме того же знака.

5) Если ряд, у которого число членов определенного знака конечно, сходится, то он сходится абсолютно.

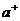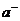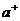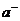6) Если у ряда число положительных и отрицательных слагаемых бесконечно и он сходится абсолютно, то ряды из и сходятся.

Функциональные ряды.

Ряд 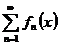, у которого слагаемыми являются функции, называется функциональным рядом. Областью определения функционального ряда является пересечение областей определения отдельных его слагаемых.

Для функциональных рядов рассматривается поточечная сходимость (т.е. ряд называется сходящимся в точке 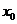, если при подстановке 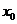вместо x получается сходящийся числовой ряд). Множество x, для которых ряд сходится, называется областью сходимости ряда.

Рассмотрим степенной ряд .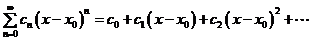

Исследуем абсолютную сходимость ряда с помощью признака Коши:

.

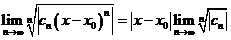Для сходимости необходимо, чтобы 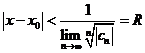, т.е. степенной ряд сходится абсолютно в круге радиуса 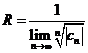. R – называется радиусом сходимости степенного ряда. Этот круг называется кругом сходимости степенного ряда. На границе круга сходимости ряд может, как сходиться, так и расходиться. Абель установил, что на границе круга сходимости (в комплексной плоскости) существует, по крайней мере одна точка, в которой ряд сходится абсолютно.

Вне круга сходимости ряд расходится, ибо общий член ряда не стремится к нулю.

С помощью признака Даламбера может быть получена еще одна формула для нахождения радиуса сходимости степенного ряда: .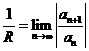

Примеры:Для следующих функциональных рядов установить области сходимости:

1°. 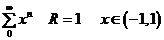; 2°. ;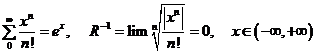

3°. ;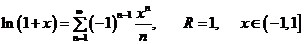

4°. ;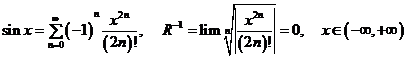

5°. ;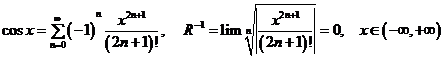

6°. 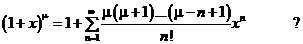.