Признаки сходимости знакопостоянных рядов.
а). Мажорантный признак.
Пусть имеется два ряда с положительными членами (знакоположительных) 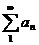 и
и 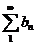 и
и
$N "n>N 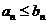 . Тогда: если ряд
. Тогда: если ряд 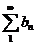 сходится Þ
сходится Þ 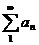 – сходится;
– сходится;
если ряд 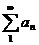 расходится Þ
расходится Þ 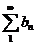 – расходится.
– расходится.
D  ▲.
▲.
б). Асимптотическая форма мажорантного признака.
Пусть "n 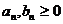 и, при n®¥,
и, при n®¥,  . Тогда: сходится
. Тогда: сходится 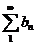 Þ сходится
Þ сходится 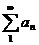 ;
;
расходится 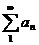 Þ расходится
Þ расходится 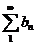 .
.
в). Асимптотический признак одновременной сходимости – расходимости рядов.
Пусть "n 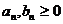 при n®¥
при n®¥  . Тогда ряды
. Тогда ряды 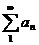 и
и 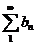 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
г). Предельная форма асимптотического признака одновременной сходимости – расходимости рядов
Пусть "n 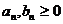 и существует, конечен и не равен нулю
и существует, конечен и не равен нулю 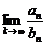 , то ряды
, то ряды 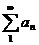 и
и 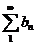 сходятся – расходятся одновременно.
сходятся – расходятся одновременно.
Интегральный признак Коши – Маклорена.
Т°. Если для знакоположительного ряда с монотонно убывающими членами, существует интегрируемая по Риману на замкнутых подпромежутках положительной полуоси, невозрастающая неотрицательная функция, совпадающая при целых значениях аргумента со значениями соответствующих членов ряда, то ряд и несобственный интеграл сходятся и расходятся одновременно. При этом разность между остатком ряда после n-го члена и интегралом по 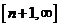 не превышает n +1 члена ряда.
не превышает n +1 члена ряда.
Δ Рассмотрим на оси абсцисс точки 1, 2, 3, …, n–1, n, n +1. И построим …..
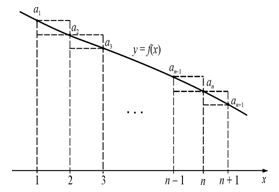 Прежде всего, отметим что
Прежде всего, отметим что 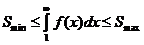 . Здесь
. Здесь 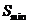 – площадь криволинейной трапеции «по недостатку», а
– площадь криволинейной трапеции «по недостатку», а 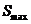 – площадь криволинейной трапеции «по избытку».
– площадь криволинейной трапеции «по избытку».
Пусть 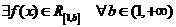 такая, что
такая, что 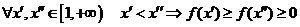 и, кроме того,
и, кроме того, 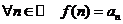 .
.
Тогда 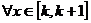
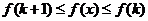 Þ
Þ 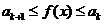 Þ
Þ  Þ
Þ
Þ 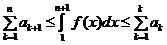 . Из этого неравенства, ясно что, если ряд
. Из этого неравенства, ясно что, если ряд 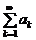 сходится, то сходится и интеграл
сходится, то сходится и интеграл 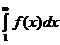 , и наоборот.
, и наоборот.
(?). Рассмотрим цепочку неравенств: 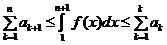 Þ
Þ  Þ
Þ
Þ 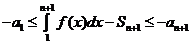 . Перейдем к пределу при
. Перейдем к пределу при 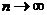 . ....... ▲
. ....... ▲
Пример 1:
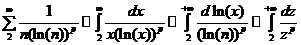 , и здесь знак эквивалентности означает, что ряды и интегралы, стоящие по разные стороны этого знака сходятся или расходятся одновременно. Тогда ряд
, и здесь знак эквивалентности означает, что ряды и интегралы, стоящие по разные стороны этого знака сходятся или расходятся одновременно. Тогда ряд  сходится при р >1 и расходится при р
сходится при р >1 и расходится при р 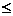 1.
1.
Пример 2: Дзета-функция Римана ζ(z).
Def: 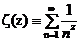 ;
; 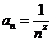 . Если
. Если 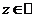 Þ
Þ 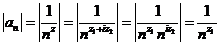 ,
,
а ряд 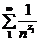 сходится или расходится одновременно с интегралом
сходится или расходится одновременно с интегралом 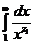 .
.
т. е. ряд 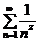 сходится, если Re z > 1 и расходится при Re z
сходится, если Re z > 1 и расходится при Re z 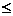 1.
1.
Признак Коши сходимости знакопостоянных рядов.
Не ограничивая общности, можно считать знакопостоянный ряд знакоположительным. Рассмотрим ряд 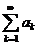 . Последовательность
. Последовательность 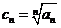 для ряда
для ряда 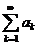 называется последовательностью Коши.
называется последовательностью Коши.
Признак Коши: Для ряда 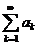 если
если 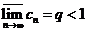 , то ряд сходится, а если
, то ряд сходится, а если 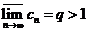 , то ряд расходится. При q = 1 признак Коши на вопрос о сходимости не отвечает.
, то ряд расходится. При q = 1 признак Коши на вопрос о сходимости не отвечает.
Предельная форма признака Коши:Если 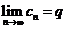 , то при
, то при 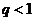 ряд сходится, при
ряд сходится, при 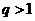 ряд расходится, при
ряд расходится, при 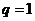 ответа на вопрос о сходимости нет.
ответа на вопрос о сходимости нет.
Δ. Пусть 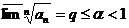 , тогда с некоторого номера
, тогда с некоторого номера 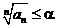 Þ
Þ 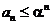 , ряд
, ряд 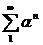 – сходится (бесконечно убывающая геометрическая прогрессия), следовательно
– сходится (бесконечно убывающая геометрическая прогрессия), следовательно 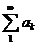 также сходится. Если же
также сходится. Если же 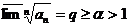 , тогда при достаточно больших n
, тогда при достаточно больших n 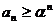
и общий член ряда не стремится к нулю. Ряд расходится. ▲
